20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2. Tọa độ của vectơ trong không gian (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong không gian Oxyz, cho vectơ \(\overrightarrow u = 3\overrightarrow i + 4\overrightarrow k - \overrightarrow j \). Tọa độ của vectơ \(\overrightarrow u \) là
(3; −1; 4).
(3; 4; −1).
(4; −1; 3).
(4; 3; −1).
Trong không gian Oxyz, cho điểm M thỏa mãn \(\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j \). Tọa độ điểm M là
M(0; 2; 1).
M(1; 2; 0).
M(2; 0; 1).
M(2; 1; 0).
Trong không gian Oxyz, xác định tọa độ của điểm A biết A nằm trên tia Ox và OA = 2.
A(0; 0; 2).
A(2; 2; 0).
A(0; 2; 0).
A(2; 0; 0).
Trong không gian Oxyz, cho hai điểm A(1; −1; 2) và B(2; 1; −4). Vectơ \(\overrightarrow {AB} \) có tọa độ là
(−1; −2; 6).
(3; 0; −2).
(1; 0; −6).
(1; 2; −6).
Cho hai điểm A, B thỏa mãn \(\overrightarrow {OA} = \left( {2; - 1;3} \right)\) và \(\overrightarrow {OB} = \left( {5;2; - 1} \right)\).Tìm tọa độ vectơ \(\overrightarrow {AB} \).
(2; −1; 3).
(3; 3; −4).
(7; 1; 2).
(3; −3; 4).
Trong không gian Oxyz, cho hai điểm M và N biết M(2; 1; −1) và \(\overrightarrow {MN} = \left( { - 1;2; - 3} \right)\). Tọa độ N là
N(1; −3; −4).
N(1; 3; −4).
N(−1; 3; −4).
(1; 3; 4).
Hình chiếu vuông góc của điểm A(3; −4; 5) trên mặt phẳng (Oxz) là điểm
M(3; 0; 0).
M(0; −4; 5).
M(0; 0; 5).
M(3; 0; 5).
Trong không gian Oxyz, cho các điểm A(1; 0; 3), B(2; 3; −4), C(−3; 1; 2). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
D(4; 2; 9).
D(−2; 4; −5).
D(6; 2; −3).
D(−4; −2; 9).
Cho hình hộp ABCD.A'B'C'D' có A(1; 0; 1), B(2; 1; 2), D(1; −1; 1), C'(4; 5; −5). Tìm tọa độ đỉnh C của hình hộp.
C(2; 2; 2).
C(2; 0; 2).
C(2; 2; 0).
C(0; 2; 2).
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' có ba đỉnh A, C, O' lần lượt nằm trên ba tia Ox, Oy, Oz và có ba cạnh OA = 6; OC = 8; OO' = 5 (tham khảo hình vẽ mình họa).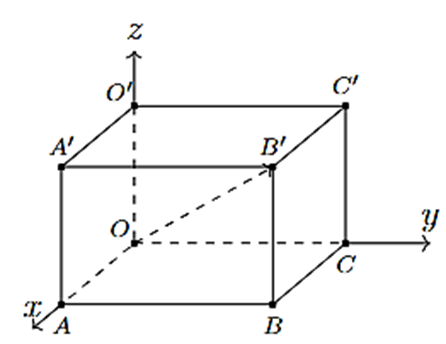
Điểm B' có tọa độ là
(8; 6; 5).
(5; 6; 8).
(6; 5; 8).
(6; 8; 5).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1; 0; −2), B(−2; 3; 4), C(4; −6; 1).
a) \(\overrightarrow {OA} = \overrightarrow i - 2\overrightarrow j \).
b) \(\overrightarrow {AB} = \left( {3; - 3; - 6} \right)\).
c) Hình chiếu vuông góc của điểm B trên mặt phẳng (Oxy) là B(−2; 3; 0).
d) Nếu ABCD là hình bình hành thì tọa độ điểm D là (1; −3; 7).
Trong không gian Oxyz, cho hình hộp OABC.O'A'B'C' có A(1; 1; −1), B(0; 3; 0), \(\overrightarrow {BC'} = \left( {2; - 6;6} \right)\). Gọi H, K lần lượt là trọng tâm của tam giác OA'O' và CB'C'.
a) \(\overrightarrow {OA} = \overrightarrow i + \overrightarrow j - \overrightarrow k \).
b) Tọa độ điểm C' là (2; −3; 6).
c) Cho điểm M thuộc mặt phẳng (Oxy). Khi độ dài đoạn thẳng AM ngắn nhất thì M(0; 0; −1).
d) Tọa độ vectơ \(\overrightarrow {HK} = \left( { - 1;2; - 1} \right)\).
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M: biết hình chiếu của M lên trục Ox là ứng với số 3; hình chiếu của M lên trục Oy ứng với số −5; hình chiếu của M lên trục Oz ứng với số 4.
a) Điểm M có tọa độ là M(3; −5; 4).
b) Điểm M1(0; 5; 0) là hình chiếu của điểm M lên trục Oy.
c) Điểm M2(3; 0; 4) là hình chiếu của điểm M lên mặt phẳng tọa độ Oxz.
d) Cho điểm M3 thỏa mãn \(\overrightarrow {O{M_3}} = - 3\overrightarrow i + 5\overrightarrow j - 4\overrightarrow k \). Vậy điểm M3 đối xứng với điểm M qua gốc tọa độ O.
Trong không gian với hệ trục tọa độ Oxyz, cho vectơ \(\overrightarrow {OA} = - 2\overrightarrow i + 3\overrightarrow k \) và B(0; −1; 6). Khi đó:
a) A(−2; 0; 3).
b) Điểm A thuộc trục hoành.
c) \(\overrightarrow {OB} = - \overrightarrow j + 6\overrightarrow k \).
d) \(\overrightarrow {AB} = \left( { - 2;3;0} \right)\).
Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' có A(1; 0; 2), B(3; 2; 5), C(7; −3; 9) và A'(5; 0; 1). Khi đó:
a) \(\overrightarrow {AA'} = \left( {4;0; - 1} \right)\).
b) \(\overrightarrow {AB} = \left( {2;2;2} \right)\).
c) \(\overrightarrow {A'C'} = \left( {6; - 3;7} \right)\).
d) B'(7; 2; 4).
PHẦN II. TRẢ LỜI NGẮN
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA = 1. Thiết lập hệ tọa độ như hình vẽ bên dưới, tọa độ điểm \(S\left( {a;\sqrt b ;c} \right)\).
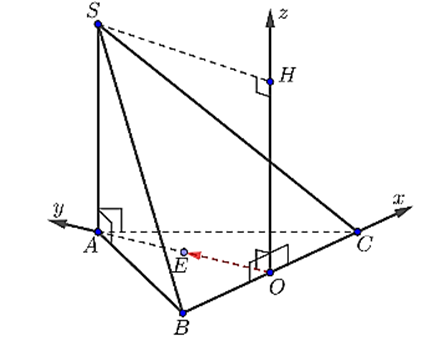
Tính a + b + c.
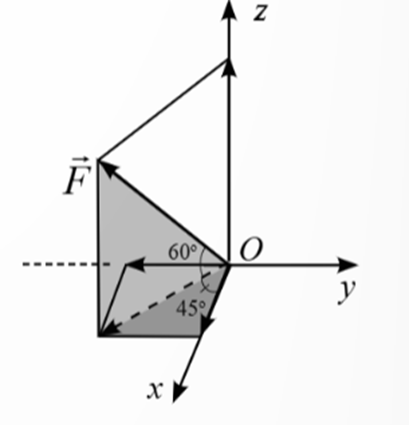
Người ta kéo vật nặng bằng một lực \(\overrightarrow F \) có cường độ 100 N (như hình). \(\overrightarrow F = \left( {a\sqrt 2 ;b\sqrt 2 ;c\sqrt 3 } \right)\) là tọa độ của vectơ \(\overrightarrow F \) trong hệ tọa độ đã cho trong hình vẽ. Tính a + b + c.
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = 4; OB = 6; OC = 8. Thiết lệp hệ trục tọa độ như hình vẽ
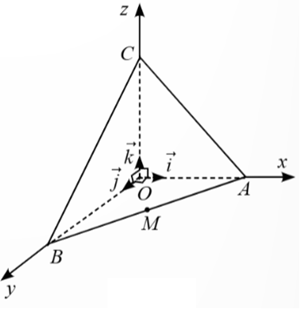
Gọi M(a; b; c) là trung điểm của AB. Tính a + b.
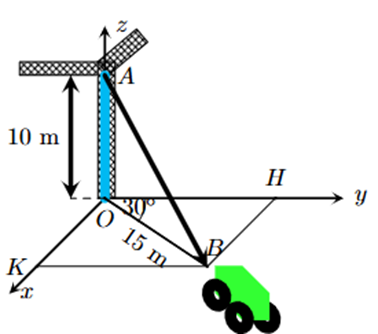
Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ Oxyz như hình bên với độ dài đơn vị trên các trục tọa độ bằng 1 (m). Biết \(\overrightarrow {AB} = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \). Hỏi giá trị của b bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
Trong không gian Oxyz, cho điểm M(2; 5; 4). Điểm M'(a; b; c) đối xứng với M qua mặt phẳng (Oyz). Tính a + b








