10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Khẳng định nào sau đây đúng?
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AB} \).
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
\(\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AC} + \overrightarrow {AD'} \).
\(\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AD'} + \overrightarrow {AA'} \).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Trong các mệnh đề sau mệnh đề nào là mệnh đề sai?
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \).
\(\overrightarrow {SA} - \overrightarrow {SB} + \overrightarrow {SC} - \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow 0 \).
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Vectơ nào bằng vectơ \(\overrightarrow {D'C'} \).
\(\overrightarrow {DD'} \).
\(\overrightarrow {AD} \).
\(\overrightarrow {AB} \).
\(\overrightarrow {CD} \).
Cho tứ diện ABCD. Chọn đẳng thức đúng.
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \).
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {DB} \).
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} \).
\(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AD} \).
Cho hình lăng trụ ABC.A'B'C'. Gọi M là trung điểm của BB'. Trong các khẳng định sau, khẳng định nào đúng?
\(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AA'} \).
\(\overrightarrow {AM} = 2\overrightarrow {AB} + \overrightarrow {AA'} \).
\(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA'} \).
\(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA'} \).
Trong không gian, cho tứ diện \(ABCD\). Ta có \[\overrightarrow {AB} \, + \,\overrightarrow {CD} \] bằng
\[\overrightarrow {AD} \, + \,\overrightarrow {BC} \].
\[\overrightarrow {DA} \, + \,\overrightarrow {CB} \] .
\[\overrightarrow {DA} \, + \,\overrightarrow {BC} \].
\[\overrightarrow {AD} \, + \,\overrightarrow {CB} \].
Trong không gian, cho hình lập phương \(ABCD\,A'B\,'C'D'\). Góc giữa hai vectơ \(\overrightarrow {BD} \,,\,\overrightarrow {B'C} \)bằng
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
\(90^\circ \).
Cho tứ diện \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SB\) vuông góc với đáy và \(SB = \sqrt 3 a\). Góc giữa hai vectơ \(\left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right)\) là
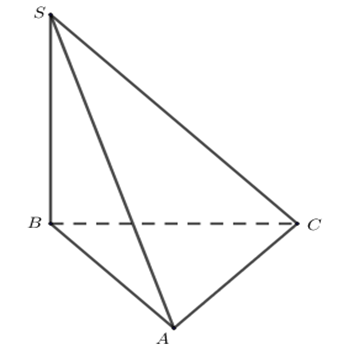
\[60^\circ \].
\[30^\circ \].
\[45^\circ \].
\[90^\circ \].
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh bằng \[a\]. Tích vô hướng của hai vectơ \[\overrightarrow {DD'} \] và \[\overrightarrow {A'C'} \] bằng
\[\sqrt 2 {a^2}\].
\[{a^2}\].
\[ - \sqrt 2 {a^2}\].
\[0\].
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng \[2\]. Tính \(\overrightarrow {AB} .\overrightarrow {A'C'} \).
![Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng \[2\]. Tính \(\overrightarrow {AB} .\overrightarrow {A'C'} \). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid9-1756112864.png)
2.
4.
−2.
−4.
