34 câu hỏi
Cho hình hộp ABCD.A'B'C'D'. Chọn khẳng định đúng trong các khẳng định dưới đây.
\[\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AD'} \].
\[\overrightarrow {CD} + \overrightarrow {CB} + \overrightarrow {CC'} = \overrightarrow {CA'} \].
\[\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DB} = \overrightarrow {DB'} \].
\[\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BD} = \overrightarrow {BD'} \].
Cho tứ diện \(ABCD\), gọi \(G\) là trọng tâm của tam giác \(BCD\). Biết luôn tồn tại số thực \(k\) thỏa mãn đẳng thức vecto \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = k.\overrightarrow {AG} \). Hỏi số thực đó bằng bao nhiêu ?
\(1\).
\(3\).
\(2\).
\(4\).
Cho tứ diện \[ABCD\]. Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của các cạnh \[AD,{\rm{ }}BC\] và \[G\] là trung điểm của \[MN\]. Mệnh đề nào sau đây đúng
\(\overrightarrow {NM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \)
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow 0 \).
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {MN} \).
Cho hình chóp S.ABCD có ABCD là hình bình hành tâm O. Trong các mệnh đề sau, mệnh đề nào đúng?
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SB} = \overrightarrow {SC} + \overrightarrow {SD} \).
Cho tứ diện \(ABCD\) có \(M,N\) lần lượt là trung điểm các cạnh \(AC\) và \(BD.\) Gọi \(G\) là trung điểm của đoạn thẳng \(MN.\) Hãy chọn khẳng định sai
\(\overrightarrow {GA} + \overrightarrow {GC} = 2\overrightarrow {GM} \).
\(\overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow {MN} \).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
\(2\overrightarrow {NM} = \overrightarrow {AB} + \overrightarrow {CD} \).
Cho tứ diện ABCD. Gọi I là trung điểm CD. Khẳng định nào sau đây đúng?
\(\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AD} \).
\(\overrightarrow {BI} = \overrightarrow {BC} + \overrightarrow {BD} \).
\(\overrightarrow {BI} = \frac{1}{2}\overrightarrow {BC} - \frac{1}{2}\overrightarrow {BD} \).
\(\overrightarrow {AI} = \overrightarrow {AC} + \overrightarrow {AD} \).
Cho hình lập phương \[B'C\] có cạnh bằng \(a\). Gọi \(O\) là tâm hình vuông \(ABCD\) và điểm \[20\] thỏa mãn \[\overrightarrow {OS} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \]. Tính độ dài đoạn \[OS\] theo \(a\).
\(OS = 6a\).
\(OS = 4a\).
\(OS = a\).
\(OS = 2a\).
Cho hình hộp ABCD.A'B'C'D'. Chọn mệnh đề sai.
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
\(\overrightarrow {AB} + \overrightarrow {B'C'} = \overrightarrow {A'C'} \).
\(\overrightarrow {BD'} = \overrightarrow {C'D'} + \overrightarrow {B'C'} + \overrightarrow {AA'} \).
\(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {CD} = \vec 0\).
Cho tứ diện \(ABCD\) có \(M,N\) lần lượt là trung điểm các cạnh \(AC\) và \(BD.\) Gọi \(G\) là trung điểm của đoạn thẳng \(MN.\) Hãy chọn khẳng định sai
\(\overrightarrow {GA} + \overrightarrow {GC} = 2\overrightarrow {GM} \).
\(G\) là trọng tâm của tứ diện \(ABCD\).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
\(\overrightarrow {GB} + \overrightarrow {GD} = 2\overrightarrow {MN} \).
Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào dưới đây là đúng ?
\(\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AD} + \overrightarrow {AA'} \).
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD'} + \overrightarrow {AA'} \).
\(\overrightarrow {A'C} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
\(\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AD} + \overrightarrow {AA'} \).
Cho tứ diện ABCD. Mệnh đề nào dưới đây là mệnh đề đúng?
\(\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {DA} - \overrightarrow {DC} \).
\(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BD} - \overrightarrow {BC} \).
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {DB} - \overrightarrow {DC} \).
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CD} + \overrightarrow {BC} \).
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành tâm O. Chọn mệnh đề đúng.
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \).
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 8\overrightarrow {SO} \).
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 2\overrightarrow {SO} \).
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {OS} \).
Hình chóp S. ABCD có đáy ABCD là hình vuông tâm O. Hãy chỉ ra mệnh đề sai?
\(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \).
\(\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \).
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
\(\overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow 0 \).
Cho hình hộp ABCD.A'B'C'D'. Gọi I, J lần lượt là trung điểm của AB' và CD'. Khẳng định nào dưới đây là khẳng định đúng?
\(\overrightarrow {D'A'} = \overrightarrow {IJ} \).
\[\overrightarrow {A'I} = \overrightarrow {JC} \].
\[\overrightarrow {AI} = \overrightarrow {CJ} \].
\[\overrightarrow {BI} = \overrightarrow {D'J} \].
Cho tứ diện ABCD và điểm G thỏa mãn \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \](G là trọng tâm của tứ diện). Gọi G0 là giao điểm của GA và mp (BCD). Trong các khẳng định sau, khẳng định nào đúng?
\[\overrightarrow {GA} = - 2\overrightarrow {{G_0}G} \].
\[\overrightarrow {GA} = 4\overrightarrow {{G_0}G} \].
\[\overrightarrow {GA} = 3\overrightarrow {{G_0}G} \].
\[\overrightarrow {GA} = 2\overrightarrow {{G_0}G} \].
Cho hình lăng trụ \[ABC.A'B'C'\]. \[M\] là trung điểm của \[BB'\]. Đặt \[\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {AA'} = \overrightarrow {c.} \] Khi đó
\[\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{{\overrightarrow b }}{2}\].
\[\overrightarrow {AM} = - \frac{{\overrightarrow a }}{2} + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AM} = - \overrightarrow a + \overrightarrow b + \frac{{\overrightarrow c }}{2}\].
\[\overrightarrow {AM} = \overrightarrow a - \frac{{\overrightarrow b }}{2} + \overrightarrow c \].
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi G là điểm thỏa mãn: \[\overrightarrow {GS} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \]. Trong các khẳng định sau, khẳng định nào đúng:
G, S, O không thẳng hàng.
\[\overrightarrow {GS} = 4\overrightarrow {OG} \].
\[\overrightarrow {GS} = 5\overrightarrow {OG} \].
\[\overrightarrow {GS} = 3\overrightarrow {OG} \].
Cho hình lăng trụ \[ABC.A'B'C'.\] \[M\] là trung điểm của \[BB'.\] Đặt \[\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {AA'} = \overrightarrow {c.} \] Khi đó
\[\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{{\overrightarrow b }}{2}\].
\[\overrightarrow {AM} = - \frac{{\overrightarrow a }}{2} + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AM} = - \overrightarrow a + \overrightarrow b + \frac{{\overrightarrow c }}{2}\].
\[\overrightarrow {AM} = \overrightarrow a - \frac{{\overrightarrow b }}{2} + \overrightarrow c \]
Cho lăng trụ tam giác \[ABC.A'B'C'\] có \[\overrightarrow {AA'} = \overrightarrow a ,\;\,\overrightarrow {AB} = \overrightarrow b ,\;\,\overrightarrow {AC} = \overrightarrow c \]. Hãy phân tích (biểu diễn) véc tơ \[\overrightarrow {BC'} \] qua các véc tơ \[\overrightarrow a ,\,\;\overrightarrow b ,\,\;\overrightarrow c \].
\[\overrightarrow {BC'} = \overrightarrow a + \overrightarrow b - \overrightarrow c \].
\[\overrightarrow {BC'} = - \overrightarrow a + \overrightarrow b - \overrightarrow c \].
\[\overrightarrow {BC'} = - \overrightarrow a - \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {BC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c \].
Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB và CD. Chọn khẳng định đúng?
\[\overrightarrow {PQ} = \frac{1}{4}\left( {\overrightarrow {BC} + \overrightarrow {AD} } \right)\].
\[\overrightarrow {PQ} = \frac{1}{2}\left( {\overrightarrow {BC} + \overrightarrow {AD} } \right)\].
\[\overrightarrow {PQ} = \frac{1}{2}\left( {\overrightarrow {BC} - \overrightarrow {AD} } \right)\].
\[\overrightarrow {PQ} = \overrightarrow {BC} + \overrightarrow {AD} \].
Cho hình lập phương\[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng?
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
\[\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
Cho hình lăng trụ \(ABC.A'B'C'\), M là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a \), \(\overrightarrow {CB} = \overrightarrow b \), \[\overrightarrow {AA'} = \overrightarrow c \] (Tham khảo hình vẽ).
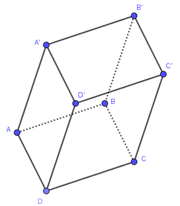 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
\(\overrightarrow {AM} = \overrightarrow a + \overrightarrow c - \frac{1}{2}\overrightarrow b \).
\(\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{1}{2}\overrightarrow b \).
\(\overrightarrow {AM} = \overrightarrow b + \overrightarrow c - \frac{1}{2}\overrightarrow a \).
\(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
Cho hình hộp \[ABCD.A'B'C'D'\]. Chọn đẳng thức đúng:
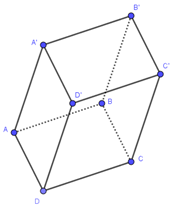
\[\overrightarrow {BD'} = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \].
\[\overrightarrow {AC'} = \overrightarrow {AC} + \overrightarrow {AB} + \overrightarrow {AD} \].
\[\overrightarrow {DB} = \overrightarrow {DA} + \overrightarrow {DD'} + \overrightarrow {DC} \].
\[\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \].
Cho hình hộp ABCD.A'B'C'D' với M là trung điểm cạnh BC (tham khảo hình vẽ bên).
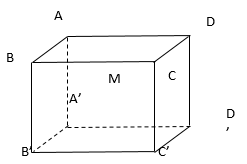 Biết \(\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {A'B'} + k\overrightarrow {BC} \). Tìm \(k\)?
Biết \(\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {A'B'} + k\overrightarrow {BC} \). Tìm \(k\)?
\(k = \frac{1}{2}\)
\(k = 2\)
\(k = - \frac{1}{2}\)
\(k = \frac{3}{2}\)
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Tìm giá trị của \(k\)thích hợp điền vào đẳng thức vectơ: \(\overrightarrow {AB} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {D{D_1}} = k\overrightarrow {A{C_1}} \)
\(k = 4\).
\(k = 1\).
\(k = 0\).
\(k = 2\).
Cho tứ diện \[ABCD\]. Đặt \[\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c ,\]gọi G là trọng tâm của tam giác \[BCD\]. Trong các đẳng thức sau, đẳng thức nào đúng?
\[\overrightarrow {AG} = \overrightarrow a + \overrightarrow b + \overrightarrow c \].
\[\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
\[\overrightarrow {AG} = \frac{1}{2}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
\[\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
Cho hình lăng trụ tam giác\(ABC.A'B'C'\). Gọi \(M\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {AA'} = \overrightarrow a ,{\rm{ }}\overrightarrow {CA} = \overrightarrow b ,{\rm{ }}\). \(\overrightarrow {CB} = \overrightarrow c \). Khẳng định nào dưới đây là đúng?
\(\overrightarrow {AM} = - \overrightarrow b + \overrightarrow c + \frac{1}{2}\overrightarrow a \).
\(\overrightarrow {AM} = \overrightarrow b + \overrightarrow c - \frac{1}{2}\overrightarrow a \).
\(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
\(\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{1}{2}\overrightarrow b \).
Cho tứ diện \[ABCD\]. Gọi \[M\] là trung điểm của đoạn thẳng \[BC\]. Đặt \[\overrightarrow {AB} = \overrightarrow a ,\,\,\overrightarrow {AC} = \overrightarrow b ,\,\,\overrightarrow {AD} = \overrightarrow c \]. Đẳng thức nào sau đây là đúng?
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow a - 2\overrightarrow b + \overrightarrow c } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( { - 2\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow a + 2\overrightarrow b - \overrightarrow c } \right)\).
Cho hình hộp \[ABCD.EFGH\] có \(\overrightarrow {AB} = \overrightarrow a ,\,\overrightarrow {AD} = \overrightarrow b ,\,\overrightarrow {AE} = \overrightarrow c .\) Gọi \(I\) là điểm thuộc đoạn thẳng \(BG\) sao cho \(4BI = BG\). Biểu thị \(\overrightarrow {AI} \) qua \(\overrightarrow a ,\,\;\overrightarrow b ,\,\;\overrightarrow c \) ta được
\(\overrightarrow {AI} = \overrightarrow a + \frac{7}{4}\overrightarrow b + \frac{7}{4}\overrightarrow c \).
\(\overrightarrow {AI} = \overrightarrow a + \frac{1}{3}\overrightarrow b + \frac{1}{3}\overrightarrow c \).
\(\overrightarrow {AI} = \overrightarrow a + \frac{1}{2}\overrightarrow b + \frac{1}{2}\overrightarrow c \).
\(\overrightarrow {AI} = \overrightarrow a + \frac{1}{4}\overrightarrow b + \frac{1}{4}\overrightarrow c \).
Cho tứ diện \(OABC\), \(M\)là trung điểm của \(BC\). Biểu thị \(\overrightarrow {AM} \) theo ba véc tơ \(\overrightarrow {OA} ,\,\overrightarrow {OB} ,\,\overrightarrow {OC} \)?
\(\overrightarrow {AM} = \overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} - \frac{1}{2}\overrightarrow {OC} .\)
\(\overrightarrow {AM} = - \overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} - \frac{1}{2}\overrightarrow {OC} .\)
\(\overrightarrow {AM} = - \overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} + \frac{1}{2}\overrightarrow {OC} .\)
\(\overrightarrow {AM} = \overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} + \frac{1}{2}\overrightarrow {OC} .\)
Cho hình lập phương \(ABCD.A'B'C'D'\). Tính \(\cos \left( {\overrightarrow {BD} ,\overrightarrow {A'C'} } \right).\)
\(\cos \left( {\overrightarrow {BD} ,\overrightarrow {A'C'} } \right) = 0\).
\(\cos \left( {\overrightarrow {BD} ,\overrightarrow {A'C'} } \right) = 1\).
\(\cos \left( {\overrightarrow {BD} ,\overrightarrow {A'C'} } \right) = \frac{1}{2}\).
\(\cos \left( {\overrightarrow {BD} ,\overrightarrow {A'C'} } \right) = \frac{{\sqrt 2 }}{2}\).
Cho hình chóp \[S.ABCD\]có đáy \[ABCD\] là hình bình hành, \[SA = SB = a\sqrt 6 \], \[CD = 2a\sqrt 2 \]. Gọi \[\varphi \] là góc giữa hai véc tơ \[\overrightarrow {CD} \] và \[\overrightarrow {AS} \]. Tính \[{\rm{cos}}\varphi \].
\[cos\varphi = - \frac{1}{{\sqrt 3 }}\].
\[cos\varphi = - \frac{2}{{\sqrt 6 }}\].
\[cos\varphi = \frac{1}{{\sqrt 3 }}\].
\[cos\varphi = \frac{2}{{\sqrt 6 }}\].
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành, \[SA = SB = 2a\], \[AB = a\]. Gọi \[\varphi \] là góc giữa hai véc tơ \[\overrightarrow {CD} \] và \[\overrightarrow {AS} \]. Tính \[\cos \varphi \].
\(\cos \varphi = - \frac{7}{8}\).
\(\cos \varphi = - \frac{1}{4}\).
\(\cos \varphi = \frac{7}{8}\).
\(\cos \varphi = \frac{1}{4}\).
Cho hình chóp \[S.ABC\] có \[SA = SB = SC\] và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \)?
\[120^\circ \].
\[45^\circ \].
\[60^\circ \].
\[90^\circ \]
