20 câu Trắc nghiệm Toán 10 Chân trời sáng tạo Bài 3. Giải tam giác và ứng dụng thực tế (Đúng-sai, trả lời ngắn) có đáp án

Một chiếc thuyền xuất phát từ cảng chạy ra biển theo một đường thẳng được 3 km thì rẽ sang phải theo hướng lệch với hướng ban đầu một góc \(45^\circ \) và đi thẳng theo hướng đó thêm 6 km nữa thì dừng lại. Hỏi tại vị trí mới này, chiếc thuyền cách vị trí xuất phát ban đầu của nó bao nhiêu kilômét? (Kết quả làm tròn đến chữ số hàng phần trăm).

Cho tam giác \[ABC\] cân tại \(A\) biết \(\widehat A = 120^\circ \) và \[AB = AC = a\]. Lấy điểm\[M\] trên cạnh \[BC\] sao cho \(BM = \frac{2}{5}BC\). Tính độ dài \[AM\].

Cho tam giác \[ABC\] có \[AC = 8\,;\,AB = 15\,;\,\cos A = \frac{4}{5}\]. Độ dài đường cao \[AH\] bằng:

Cho tam giác \[ABC\] có \[BC = a = 109\], \[\widehat B = 33^\circ 24'\], \[\widehat C = 66^\circ 59'\]. Chu vi tam giác \[ABC\] gần bằng số nào sau đây?

Tam giác \[ABC\] có \(\cos \left( {A + B} \right) = - \frac{1}{5}\), \[AC = 6\], \[BC = 5\]. Tính độ dài cạnh \[AB\].

Tam giác \[ABC\] có \[BC = 12\], \[CA = 9\], \[AB = 6\]. Trên cạnh \[BC\] lấy điểm \[M\] sao cho \[BM = 8\]. Tính độ dài đoạn thẳng \[AM\].

Khoảng cách từ \(A\) đến \(B\) không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm \(C\) mà từ đó có thể nhìn được \(A\) và \(B\) dưới một góc \(78^\circ 24'\). Biết \(CA = 250\,{\rm{m}},CB = 120\,{\rm{m}}\). Khoảng cách \(AB\) gần nhất với giá trị nào dưới đây?

Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24 m, \(\widehat {CAD} = 63^\circ \); \(\widehat {CBD} = 48^\circ \).

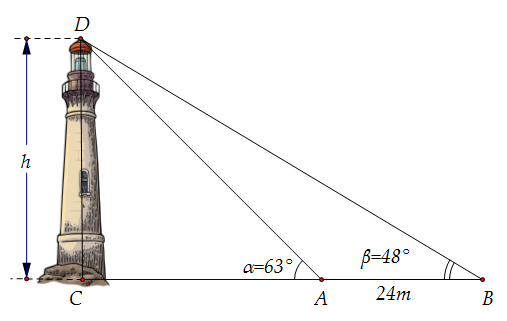
Chiều cao h của khối tháp gần với giá trị nào sau đây?

Từ vị trí \[A\] người ta quan sát một cây cao.

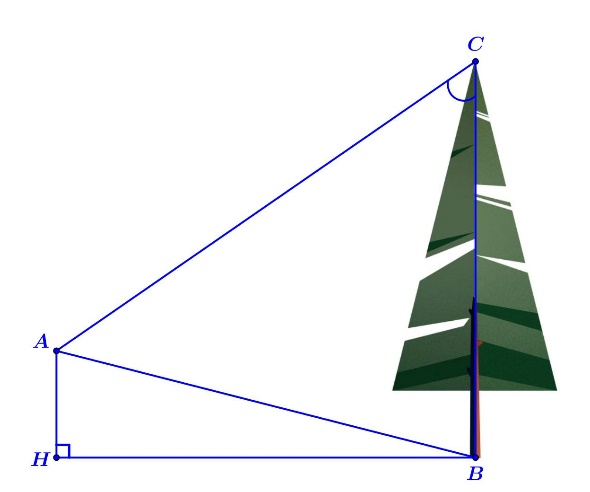
Biết \[AH = 4{\rm{m}}\], \[HB = 20{\rm{m}}\], \[\widehat {BAC} = 45^\circ \]. Khi đó chiều cao của cây (làm tròn đến hàng phần mười) bằng

Cho \(\Delta ABC\) có \(\widehat A = 135^\circ ,\widehat C = 15^\circ \) và \(AC = 12\).

a) \(\widehat B = 30^\circ \).

b) \(BC = 12\sqrt 2 \).

c) \(AB \approx 8,21\).

d) Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là \(R = 15\).

Cho tam giác \(ABC\) biết \(BC = 3\;{\rm{cm}},\,\,AC = 4{\rm{\;cm}},\widehat C = 30^\circ \).

a) \(AB \approx 3,05\,\,{\rm{(cm)}}\).

b) \(\cos A \approx 0,68\).

c) \(\widehat A \approx 77,2^\circ \).

d) \(\widehat B \approx 102,8^\circ \).

Cho tam giác \(ABC\) biết cạnh \(BC = 137,5\;\,{\rm{cm;}}\,\widehat B = 83^\circ ;\,\,\widehat C = 57^\circ \).

a) \(\widehat A = 40^\circ \).

b) Bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R \approx 106,96{\rm{\;cm}}\).

c) \(AB \approx 179,4\,\,{\rm{cm}}\).

d) \[AC \approx 232,12{\rm{\;cm}}\].

Một người quan sát đứng cách một cái tháp \(10\,\,{\rm{m}}\), nhìn thẳng cái tháp dưới một góc \(55^\circ \) và được phân tích như trong hình.

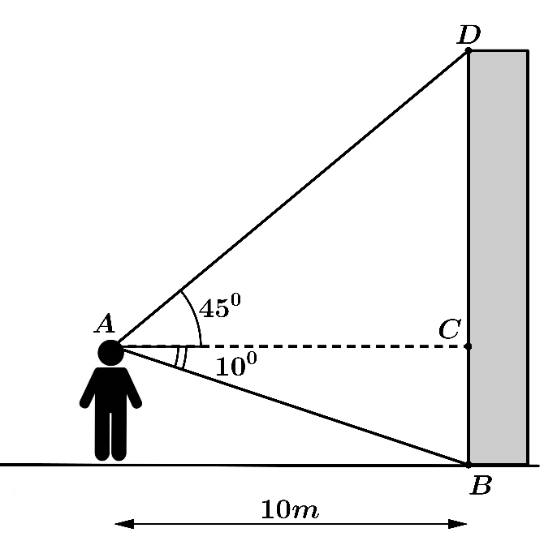
a) \(\widehat {ADC} = 45^\circ \).

b) Độ dài đoạn \(AB\) xấp xỉ bằng \(10,15\,\,{\rm{m}}\).

c) Diện tích \(\Delta ACD\) bằng \(100\,\,{{\rm{m}}^{\rm{2}}}\).

d) Chiều cao của tháp xấp xỉ bằng \(11,76\,\,{\rm{m}}\).

Cho tam giác \(ABC\) có \(\cos A = \frac{1}{3}\), \(BC = 9\) và \(AC = 6\), \(M\) là trung điểm cạnh \(BC\).

a) Độ dài cạnh \(AB = 8\).

b) Diện tích hình tròn ngoại tiếp tam giác \(ABC\) là \({S_{{\rm{ht1}}}} = 9\pi \).

c) Giá trị \(\cos \widehat {AMB}\) bằng \(\frac{{\sqrt 3 }}{5}\).

d) Tính diện tích của hình tròn nội tiếp tam giác \(ABC\) là \({S_{{\rm{ht2}}}} = \pi {r^2} = \frac{{9\pi }}{2}\).

Hai bạn An và Bình cùng xuất phát từ điểm \[P\], đi theo hai hướng khác nhau và tạo với nhau một góc \(40^\circ \) để đến đích là điểm \[D\] với \[\widehat {PAD} = 100^\circ \]. Biết rằng An và Bình dừng lại để ăn trưa lần lượt tại \[A\] và \[B\] (như hình vẽ minh hoạ).

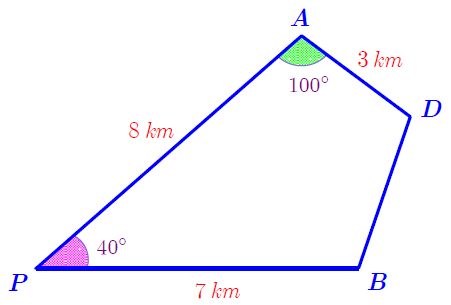
Hỏi bạn Bình phải đi bao xa nữa để đến được đích (số làm tròn đến hàng phần trăm; góc làm tròn đến hàng đơn vị)?

Tỉnh \(A\) và \(B\) bị ngăn cách nhau bởi một ngọn núi. Để đi từ tỉnh \(A\) đến tỉnh \(B\), người ta đi theo lộ trình từ tỉnh \(A\) qua tỉnh \(C\), rồi đến tỉnh \(B\). Biết rằng lộ trình từ \(A\) đến \(C\) dài 70 km, từ \(C\) đến \(B\) dài 100 km, và hai con đường tạo với nhau góc \(60^\circ \). Cứ mỗi 20 km quãng đường thì phương tiện tiêu hao 1 lít nhiên liệu. Để tiết kiệm nhiên liệu, người ta làm một đường hầm xuyên núi để đi từ tỉnh \(A\) đến tỉnh \(B\). Hỏi nếu đi theo đường hầm thì phương tiện tiết kiệm được bao nhiêu lít nhiên liệu (làm tròn kết quả đến hàng phần trăm)?

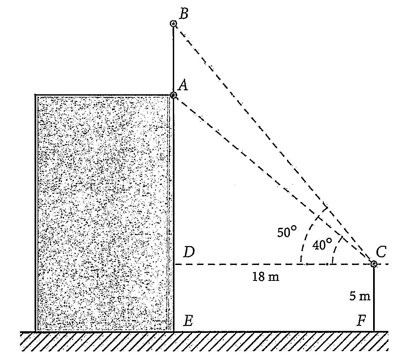
Để đo chiều cao của một cột cờ trên đỉnh một toà nhà anh Bắc đã làm như sau: Anh đứng trên một đài quan sát có tầm quan sát cao \(5\;\,{\rm{m}}\) so với mặt đất. Khi quan sát, anh Bắc đo được góc quan sát chân cột là \(40^\circ \) và góc quan sát đỉnh cột là \(50^\circ \), khoảng cách từ chân toà nhà đến vị trí quan sát là \(18\;\,{\rm{m}}\). Tính chiều cao cột cờ (làm tròn đến hàng phần trăm).

Gia đình bác An có mảnh đất như hình bên dưới. Nhà nước có dự án xây bệnh viện nên thu hồi mảnh đất của bác, giá đền bù là \(1,2\) triệu đồng 1\({{\rm{m}}^{\rm{2}}}\).

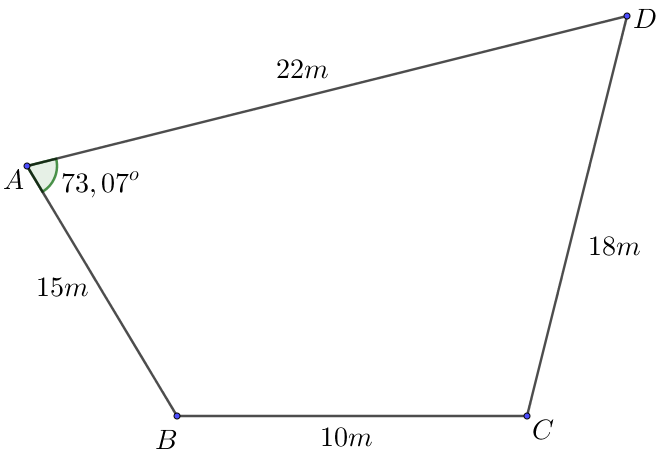
Hỏi số tiền gia đình nhà bác An nhận được khoảng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).

Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng \(N80^\circ E\) với vận tốc \(20\,\,{\rm{km/h}}\). Sau khi đi được 30 phút, tàu chuyển sang hướng \(E80^\circ S\) giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà (tham khảo hình vẽ). Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu kilômét? (Kết quả làm tròn đến hàng phần mười).