10 câu hỏi
Khi giải tam giác \(ABC\) biết \(\,\widehat A = 15^\circ ,\,\,\widehat B = 130^\circ ,\,c = 6.\) Ta có kết quả là:
\(\widehat C = 35^\circ ;a \approx 2,71;b \approx 8,01\).
\(a \approx 2,71;b \approx 8,01\).
\(\widehat C = 35^\circ ;a = 2,71;b = 8\).
\(a = 2,71;b = 8\).
Một chiếc thuyền xuất phát từ cảng chạy ra biển theo một đường thẳng được 3 km thì rẽ sang phải theo hướng lệch với hướng ban đầu một góc \(45^\circ \) và đi thẳng theo hướng đó thêm 6 km nữa thì dừng lại. Hỏi tại vị trí mới này, chiếc thuyền cách vị trí xuất phát ban đầu của nó bao nhiêu kilômét? (Kết quả làm tròn đến chữ số hàng phần trăm).
\(4,42\,{\rm{km}}.\)
\(19,54\,{\rm{km}}.\)
\(8,39\,{\rm{km}}\).
\(70,46\,\,{\rm{km}}.\)
Cho tam giác \[ABC\] cân tại \(A\) biết \(\widehat A = 120^\circ \) và \[AB = AC = a\]. Lấy điểm\[M\] trên cạnh \[BC\] sao cho \(BM = \frac{2}{5}BC\). Tính độ dài \[AM\].
\(AM = \frac{{a\sqrt 3 }}{3}\).
\(AM = \frac{{11a}}{5}\).
\(AM = \frac{{a\sqrt 7 }}{5}\).
\(AM = \frac{{a\sqrt 6 }}{4}\).
Cho tam giác \[ABC\] có \[AC = 8\,;\,AB = 15\,;\,\cos A = \frac{4}{5}\]. Độ dài đường cao \[AH\] bằng:
\[\frac{{72}}{{\sqrt {79} }}\].
\[\frac{{72}}{{97}}\].
\[\frac{{\sqrt {72} }}{{97}}\].
\[\frac{{72}}{{\sqrt {97} }}\].
Cho tam giác \[ABC\] có \[BC = a = 109\], \[\widehat B = 33^\circ 24'\], \[\widehat C = 66^\circ 59'\]. Chu vi tam giác \[ABC\] gần bằng số nào sau đây?
\[136\].
\[227\].
\[272\].
\[372\].
Tam giác \[ABC\] có \(\cos \left( {A + B} \right) = - \frac{1}{5}\), \[AC = 6\], \[BC = 5\]. Tính độ dài cạnh \[AB\].
\(\sqrt {73} \).
\[8\].
\(\sqrt {55} \).
\[7\].
Tam giác \[ABC\] có \[BC = 12\], \[CA = 9\], \[AB = 6\]. Trên cạnh \[BC\] lấy điểm \[M\] sao cho \[BM = 8\]. Tính độ dài đoạn thẳng \[AM\].
\(\sqrt {94} \).
\[\sqrt {106} \].
\(\sqrt {166} \).
\[\sqrt {34} \].
Khoảng cách từ \(A\) đến \(B\) không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm \(C\) mà từ đó có thể nhìn được \(A\) và \(B\) dưới một góc \(78^\circ 24'\). Biết \(CA = 250\,{\rm{m}},CB = 120\,{\rm{m}}\). Khoảng cách \(AB\) gần nhất với giá trị nào dưới đây?
\(266\,\,{\rm{m}}.\)
\(255\,\,{\rm{m}}.\)
\(166\,\,{\rm{m}}.\)
\(298\,{\rm{m}}.\)
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24 m, \(\widehat {CAD} = 63^\circ \); \(\widehat {CBD} = 48^\circ \).
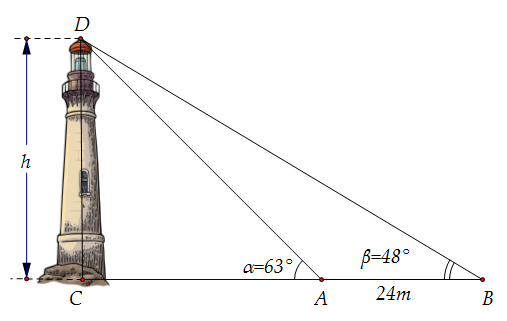
Chiều cao h của khối tháp gần với giá trị nào sau đây?
61,4 m.
18,5 m.
60 m.
18 m.
Từ vị trí \[A\] người ta quan sát một cây cao.
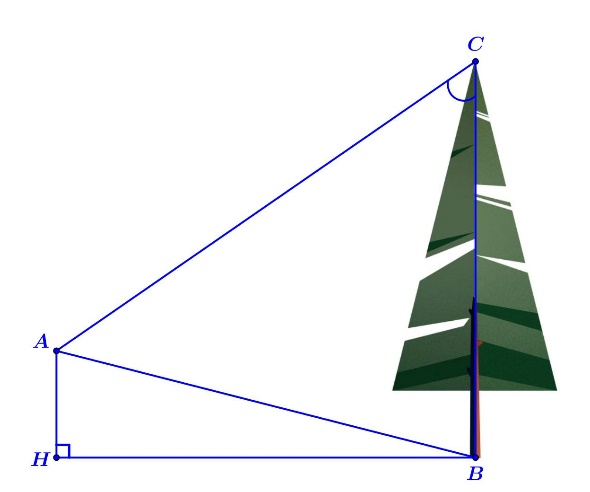
Biết \[AH = 4{\rm{m}}\], \[HB = 20{\rm{m}}\], \[\widehat {BAC} = 45^\circ \]. Khi đó chiều cao của cây (làm tròn đến hàng phần mười) bằng
\[17,3{\rm{m}}\].
\[17,6{\rm{m}}\].
\[17,2{\rm{m}}\].
\[17,4{\rm{m}}\].
