Quiz

184 câu Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác có đáp án (Mới nhất)

VietJackToánLớp 117 lượt thi

Bắt đầu ngay

170 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định của hàm số $y = \frac{1 - 2 x}{\sin 2 x}$ .

$D = ℝ \ \{k π, k \in ℤ\}$

$D = ℝ \ \{\frac{π}{2} + k 2 π, k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

$D = ℝ \ \{k \frac{π}{2}, k \in ℤ\}$ .

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định của hàm số $y = \frac{3}{\cos x + 1}$

$D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{π + k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{π + k π, k \in ℤ\}$ .

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \sqrt{\sin x - 1}$ là

$ℝ$ .

$\{k π | k \in ℤ\}$ .

$\{\frac{π}{2} + k 2 π | k \in ℤ\}$ .

$\{\frac{π}{2} + k π | k \in ℤ\}$ .

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{1}{\sqrt{1 - \sin x}}$ .

$D = ℝ \ \{k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{π + k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

$D = ℝ \ \{- \frac{π}{2} + k 2 π, k \in ℤ\}$ .

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định D của hàm số $y = \tan 3 x$ là

$D = ℝ \ \{\frac{k π}{3}, k \in ℤ\}$ .

$D = ℝ \ \{\frac{π}{6} + \frac{k π}{3}, k \in ℤ\}$ .

$D = ℝ \ \{k π, k \in ℤ\}$ .

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định của hàm số $y = \frac{\tan x}{\sin x - 1}$

$ℝ .$

$ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

$ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

$ℝ \ \{k π, k \in ℤ\}$ .

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \tan (2 x + \frac{π}{6})$ là

$ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

$ℝ \ \{\frac{- π}{6} + \frac{k π}{2}, k \in ℤ\}$ .

$ℝ \ \{\frac{π}{6} + k π, k \in ℤ\}$ .

$ℝ \ \{\frac{π}{6} + \frac{k π}{2}, k \in ℤ\}$ .

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định của hàm số $y = \sqrt{1 - \cos x} + \cot x$ .

$ℝ \ \{k π, k \in ℤ\}$ .

$(- \infty; 1]$ .

$ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

$[- 1; 1] \ \{0\}$ .

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \sqrt{\frac{\sin x - 1}{3 + \sin x}}$ có tập xác định là

$ℝ \ \{\frac{π}{2} + k 2 π | k \in ℤ\}$

$ℝ$ .

$\emptyset$ .

$\{\frac{π}{2} + k 2 π | k \in ℤ\}$ .

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định của hàm số $y = \sqrt{\frac{1 + \cos x}{1 - \sin x}}$ .

$ℝ \ \{k π | k \in ℤ\}$ .

$ℝ \ \{\frac{π}{2} + k 2 π | k \in ℤ\}$ .

$ℝ$ .

$ℝ \ \{k 2 π | k \in ℤ\}$ .

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \frac{\cot x}{\cos x - 1}$ là

$ℝ \ \{k \frac{π}{2}, k \in ℤ\}$ .

$ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

$ℝ \ \{k π, k \in ℤ\}$ .

$ℝ \ \{k 2 π, k \in ℤ\}$ .

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $f (x) = \frac{1}{1 - \cos x}$ là

$ℝ \ \{(2 k + 1) \frac{π}{2} |k \in ℤ\}$ .

$ℝ \ \{(2 k + 1) π |k \in ℤ\}$ .

$ℝ \ \{k π |k \in ℤ\}$ .

$ℝ \ \{k 2 π |k \in ℤ\}$ .

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{1}{\sin (x - \frac{π}{2})}$

$D = R \ \{(2 k + 1) π, k \in ℤ\}$

$D = R \ \{\frac{k π}{2}, k \in ℤ\}$

$D = R \ \{(2 k + 1) \frac{π}{2}, k \in ℤ\}$

$D = R \ \{k π, k \in ℤ\}$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \frac{\tan 2 x}{1 - \tan x}$ có tập xác định là

$ℝ$ .

$ℝ \ \{\frac{π}{4} + k \frac{π}{2} | k \in ℤ\}$ .

$ℝ \ \{\frac{π}{2} + k π | k \in ℤ\}$ .

$ℝ \ \{\frac{π}{4} + k \frac{π}{2}, \frac{π}{2} + k π | k \in ℤ\}$ .

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \frac{3 + \cot \frac{x}{2}}{\cos x + 1}$ là:

$ℝ \ \{k π |k \in ℤ\} .$

$ℝ \ \{k 2 π |k \in ℤ\} .$

$ℝ \ \{π + k 2 π |k \in ℤ\} .$

$ℝ \ \{\frac{π}{2} + k 2 π |k \in ℤ\} .$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho các hàm số

$(1) y = \sin 3 x . (2) y = \frac{\tan x + 3}{\cos^{2} x + 2} . (3) y = \frac{2 \cos x - 1}{\sin^{2} x + 1}$

$(4) y = \sqrt{1 - \sin x} . (5) y = \sqrt{\frac{2 \cos x + 3}{\sin x + 1}} .$

Trong các hàm số trên có bao nhiêu hàm số có tập xác định là $ℝ$

4 .

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \frac{\cos x - 2}{1 + \sin x}$ là

$ℝ \ \{k π | k \in ℤ\}$ .

$ℝ \ \{- \frac{π}{2} + k π | k \in ℤ\}$ .

$ℝ \ \{k 2 π | k \in ℤ\}$ .

$ℝ \ \{- \frac{π}{2} + k 2 π | k \in ℤ\}$ .

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \frac{1}{\sqrt{s inx + 1}}$ là

$ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

$ℝ \ \{- \frac{π}{2} + k 2 π, k \in ℤ\}$ .

$ℝ \ \{- \frac{π}{2} + k π, k \in ℤ\}$ .

$ℝ$ .

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = \frac{s inx + 1}{s inx - 2}$ là

$(- 2; + \infty)$

$(2; + \infty)$

$ℝ \ \{2\}$ .

$ℝ$ .

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \frac{2 \sin x + 1}{1 - \cos x}$ xác định khi

$x \neq \frac{π}{2} + k 2 π$ .

$x \neq k π$ .

$x \neq k 2 π$ .

$x \neq \frac{π}{2} + k π$

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các mệnh đề sau, mệnh đề nào đúng?

Các hàm số $y = \sin x, y = \cos x, y = \cot x$ đều là hàm số chẵn.

Các hàm số $y = \sin x, y = \cot x, y = \tan x$ đều là hàm số lẻ.

Các hàm số $y = \sin x, y = \cot x, y = \tan x$ đều là hàm số chẵn.

Các hàm số $y = \sin x, y = \cos x, y = \cot x$ đều là hàm số lẻ.

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây là hàm số chẵn?

y= cot 4x.

$y = \tan 6 x$ .

$y = \sin 2 x$ .

$y = \cos x$ .

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau đây, hàm số nào có đồ thị đối xứng qua trục tung?

$y = \tan x$ .

$y = \cos x$ .

$y = \sin x$ .

$y = \cot x$ .

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = \cos x$ .

$y = \tan x$ .

$y = s i n x$ .

$y = \cot x$ .

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số lẻ?

$y = 1 + \sin x$ .

$y = x . \tan x$ .

$y = \sin^{5} x$ .

$y = \cos x . \sin^{2} x$ .

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây là hàm số chẵn?

$y = - 2 \sin x$ .

$y = 2 \sin 2 x$ .

$y = \sin x - \cos x$ .

$y = - 2 \cos x$

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn trên $ℝ$ ?

$y = \sin (\frac{π}{2} - x)$ .

$y = \tan x$ .

$y = \sin x$ .

$y = \sin (x + \frac{π}{6})$ .

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \frac{1}{\cos x}$ . Phát biểu nào sau đây đúng?

Hàm số có tập xác định là $ℝ \ \{0\}$ .

Đồ thị của hàm số nhận trục tung làm trục đối xứng.

Hàm số đó là hàm số lẻ trên $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

Hàm số đó là hàm số lẻ trên $ℝ$ .

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số lẻ?

$y = x^{2} \cos x$ .

$y = \sin 2 x$ .

$y = \sin^{2} x$ .

$y = \cos 2 x$ .

Xem đáp án

30. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào không là hàm số chẵn và cũng không là hàm số lẻ?

$y = \sin (x + \frac{π}{4}) + \tan (x + \frac{π}{4})$ .

$y = \tan x - \frac{1}{\sin x}$ .

$y = \sin^{4} x - \cos^{4} x$ .

$y = \cos x$ .

Xem đáp án

31. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây là hàm số chẵn.

$y = \cot x$ .

$y = \sin x$ .

$y = \tan x$ .

$y = \cos x$

Xem đáp án

32. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm chẵn?

$y = \cos (x + \frac{π}{3})$ .

$y = |\sin x|$ .

$y = 1 - \sin x$ .

$y = \sin x + \cos x$ .

Xem đáp án

33. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = \tan x$ .

$y = \sin x$ .

$y = \cos x$ .

$y = \cot x$ .

Xem đáp án

34. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây là hàm số tuần hoàn với chu kỳ $T = π$ ?

$y = \sin x$ .

$y = 2 \sin x$ .

$y = \sin 2 x$ .

$y = 2 + \sin x$ .

Xem đáp án

35. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây tuần hoàn với chu kì $T = \frac{π}{2}$ ?

$y = \tan \frac{x}{3}$ .

$y = \tan \frac{x}{2}$ .

$y = \tan 3 x$ .

$y = \tan 2 x$ .

Xem đáp án

36. Trắc nghiệm

• 1 điểm • Không giới hạn

Chọn khẳng định sai?

Hàm số $y = \tan x + \sin x$ là hàm số tuần hoàn với chu kì $2 π .$

Hàm số $y = \cos x$ là hàm số tuần hoàn với chu kì $2 π .$

Hàm số $y = \cot x + \tan x$ là hàm số tuần hoàn với chu kì $π .$

Hàm số $y = \sin x$ là hàm số tuần hoàn với chu kì $π$

Xem đáp án

37. Trắc nghiệm

• 1 điểm • Không giới hạn

Chu kỳ tuần hoàn của hàm số $y = \cot (3 x + \frac{π}{6})$ là

$π$ .

$\frac{2 π}{3}$ .

$\frac{π}{3}$ .

$2 π$ .

Xem đáp án

38. Trắc nghiệm

• 1 điểm • Không giới hạn

Khẳng định nào sau đây đúng?

Hàm số $y = \sin x$ tuần hoàn với chu kì $π$ .

Hàm số $y = \tan x$ tuần hoàn với chu kì $2 π$ .

Hàm số $y = \cos x$ tuần hoàn với chu kì $\frac{π}{2}$ .

Hàm số $y = \cot x$ tuần hoàn với chu kì $π$ .

Xem đáp án

39. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong bốn hàm số: $(1) y = \cos 2 x; (2) y = \sin x; (3) y = \tan 2 x; (4) y = \cot 4 x$ có mấy hàm số tuần hoàn với chu kỳ $π$ ?

Xem đáp án

40. Trắc nghiệm

• 1 điểm • Không giới hạn

Khẳng định nào sai trong các khẳng định sau?

$y = \cos x$ tuần hoàn với chu kỳ $π$ .

$y = \cos x$ là hàm nghịch biến trên $(0; π)$ .

$y = \cos x$ là hàm chẵn.

$y = \cos x$ có tập xác định $ℝ$ .

Xem đáp án

41. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \frac{1}{1 + \tan^{2} x} + \frac{1}{1 + \cot^{2} 2 x}$ có chu kì là:

$T = \frac{π}{2}$ .

$T = 2 π$ .

$T = π$ .

$T = 4 π$ .

Xem đáp án

42. Trắc nghiệm

• 1 điểm • Không giới hạn

Chu kì tuần hoàn của hàm số $y = \cot x$ là

$π$ .

$2 π$ .

$k π$ , ( $k \in ℤ$ ).

$k 2 π$ , ( $k \in ℤ$ ).

Xem đáp án

43. Trắc nghiệm

• 1 điểm • Không giới hạn

Chu kỳ tuần hoàn của hàm số $y = \tan x$ là

$2 π$

$π$

$\frac{π}{2}$

$3 π$

Xem đáp án

44. Trắc nghiệm

• 1 điểm • Không giới hạn

Chu kỳ tuần hoàn của hàm số $y = \cos x$

$T = \frac{π}{2}$ .

$T = π$ .

$T = 2$ .

$T = 2 π$ .

Xem đáp án

45. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 3 \cos 2 x - 5$ lần lượt là

$- 8$ và -2 .

2và 8 .

-5và 3 .

-5và 2 .

Xem đáp án

46. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 7 - 2 \sin (x + \frac{π}{4})$ lần lượt là

4và 7.

5và 9.

-2và 7.

-2và 2.

Xem đáp án

47. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập giá trị của hàm số $y = 2 \cos 3 x + 1$ .

$[- 3; 1]$ .

$[- 3; - 1]$ .

$[- 1; 3]$ .

$[1; 3]$ .

Xem đáp án

48. Trắc nghiệm

• 1 điểm • Không giới hạn

Tổng giá trị lớn nhất và nhỏ nhất của hàm số $y = 3 \cos x + 4$ là

Xem đáp án

49. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị nhỏ nhất của hàm số: $y = 3 \sin (x + \frac{π}{4})$ là:

-3.

-1.

Xem đáp án

50. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \sin x$ có tập giá trị là:

$ℝ$ .

$[- 1; 1]$ .

$[- π; π]$ .

$[0; π]$

Xem đáp án

51. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị lớn nhất của hàm số $y = 2 \sin x + 1$ là

$- 1$ .

$1$ .

$- \frac{1}{2}$ .

$3$ .

Xem đáp án

52. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = 4 \sqrt{\sin x + 3} - 1$ lần lượt là

$\sqrt{2}$ và $2$ .

$4 \sqrt{2}$ và $8$ .

$2$ và 4.

$4 \sqrt{2} - 1$ và $7$ .

Xem đáp án

53. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = 2 - \cos^{2} x$ là

2và -1.

2và 0.

2và 1.

3và 1.

Xem đáp án

54. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \sin x$ trên đoạn $[\frac{- 3 π}{2}; \frac{5 π}{2}]$ có đồ thị như hình vẽ. Tìm những giá trị x để hàm số nhận giá trị âm.

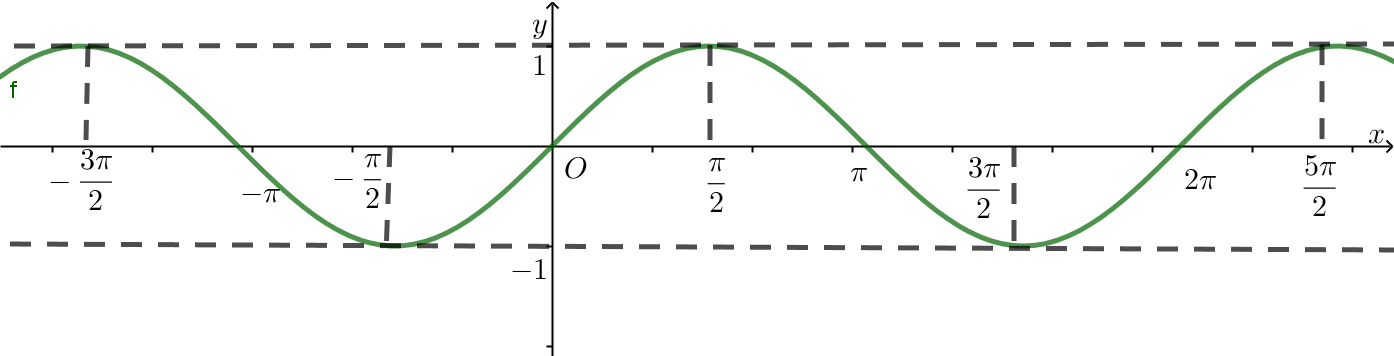
Media VietJack

A. .

B. .

C. .

D. .

Xem đáp án

55. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị lớn nhất, nhỏ nhất của hàm số $y = 3 - 2 \cos^{2} x$ lần lượt là

$y_{\max} = 5, y_{\min} = 1$ .

$y_{\max} = 1, y_{\min} = - 1$ .

$y_{\max} = 3, y_{\min} = 1$ .

$y_{\max} = 5, y_{\min} = - 1$ .

Xem đáp án

56. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M của hàm số $y = 2 \cos x - \sin x$ .

$M = \sqrt{\frac{11}{2}}$ .

$M = \sqrt{5}$ .

$M = \sqrt{3}$ .

$M = \sqrt{6}$ .

Xem đáp án

57. Trắc nghiệm

• 1 điểm • Không giới hạn

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sqrt{2} \cos 2 x - 1$ trên đoạn $[- \frac{π}{6}; \frac{3 π}{8}]$ . khi đó $M . m$ bằng

-1.

$2 - 2 \sqrt{2} .$

$2 - \sqrt{2} .$

$2 \sqrt{2} - 2.$

Xem đáp án

58. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập giá trị hàm số y= 5sinx- 12cosx là

$[- 12; 5]$ .

$[- 13; 13]$ .

$[- 17; 17]$ .

$(- 13; 13)$ .

Xem đáp án

59. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = 4 - 11 \cos^{3} x$ có tất cả bao nhiêu giá trị nguyên dương?

15.

14.

13.

23.

Xem đáp án

60. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị lớn nhất của hàm số $y = 5 \sin 2 x + 12 \cos 2 x$ là

10.

12.

17.

13.

Xem đáp án

61. Trắc nghiệm

• 1 điểm • Không giới hạn

Đồ thị trong hình vẽ dưới đây là của hàm số nào?

Media VietJack

$y = \cot x$ .

$y = \sin 2 x$ .

$y = \sin x$ .

$y = \cos 2 x$ .

Xem đáp án

62. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho đồ thị với $x \in [- π; π]$ . Đây là đồ thị của hàm số của hàm số nào?

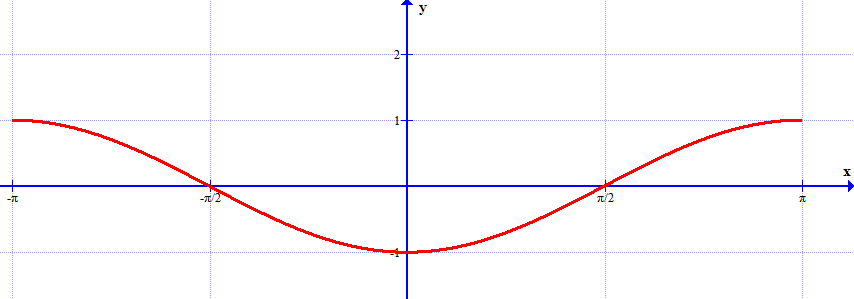
Media VietJack

$y = \cos x$ .

$y = - \cos x$ .

$y = \sin x$ .

$y = \cos |x|$

Xem đáp án

63. Trắc nghiệm

• 1 điểm • Không giới hạn

Dựa vào đồ thị của hàm số $y = \sin x$ , hãy tìm số nghiệm của phương trình: $\sin x = \frac{1}{2018}$ trên đoạn $[\frac{- 5 π}{2}; \frac{5 π}{2}]$ .

Media VietJack

10.

Xem đáp án

64. Trắc nghiệm

• 1 điểm • Không giới hạn

Hình bên là một phần đồ thị của hàm số nào sau đây?

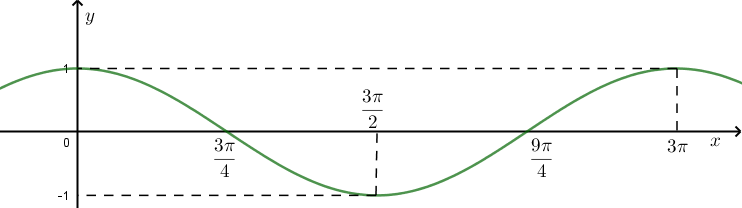
Media VietJack

$y = \cos \frac{2 x}{3}$ .

$y = \sin \frac{2 x}{3}$ .

$y = \cos \frac{3 x}{2}$

$y = \sin \frac{3 x}{2}$

Xem đáp án

65. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,D.

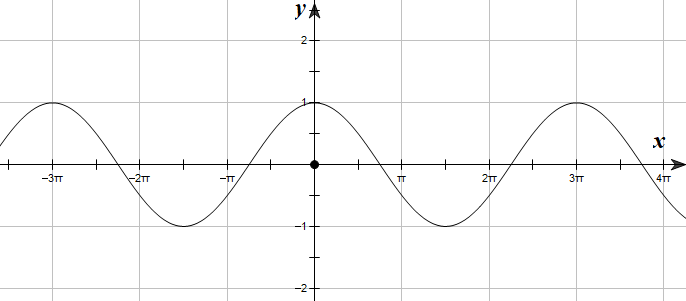
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \sin \frac{3 x}{2} .$

$y = \sin \frac{2 x}{3} .$

$y = cos \frac{3 x}{2} .$

$y = cos \frac{2 x}{3} .$

Xem đáp án

66. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm mệnh đề sai trong các mệnh đề sau.

Hàm số $y = \cos x$ tuần hoàn với chu kì $2 π$ .

Hàm số $y = \sin x$ nghịch biến trên khoảng $(\frac{π}{2}; π)$ .

Hàm số $y = \cot x$ đồng biến trên khoảng $(\frac{π}{2}; π)$ .

Hàm số $y = \tan x$ tuần hoàn với chu kì $π$ .

Xem đáp án

67. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \tan x$ đồng biến trên khoảng nào dưới đây?

$(0; π)$ .

$(- \frac{3 π}{2}; - \frac{π}{2})$ .

$(- \frac{3 π}{2}; \frac{π}{2})$

$(- 2 π; - π)$ .

Xem đáp án

68. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm mệnh đề đúng trong các mệnh đề sau?

Hàm số $y = \cot x$ đồng biến trên khoảng $(0; π)$ .

Hàm số $y = \sin x$ đồng biến trên khoảng $(\frac{3 π}{2}; \frac{5 π}{2})$ .

Hàm số $y = \sin x$ nghịch biến trên khoảng $(π; 2 π)$ .

Hàm số $y = \cos x$ đồng biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ .

Xem đáp án

69. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \sin x$ . Khẳng định nào dưới đây sai?

Hàm số đã cho là hàm lẻ.

Hàm số đã cho có tập giá trị là $[- 1; 1]$ .

Hàm số đã cho đồng biến trên $(0; 2 π)$ .

Hàm số đã cho có tập xác định $ℝ$ .

Xem đáp án

70. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho ba hàm số $y = s in x; y = cos x; y = tan x$ . Có bao nhiêu hàm số đồng biến trên $(0; \frac{3 π}{2})$ ?

Xem đáp án

71. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{2019}{\sin x} .$

$D = ℝ .$

$D = ℝ \ \{0\} .$

$D = ℝ \ \{k π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

Xem đáp án

72. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{1 - \sin x}{\cos x - 1} .$

$D = ℝ .$

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

$D = ℝ \ \{k π, k \in ℤ\} .$

$D = ℝ \ \{k 2 π, k \in ℤ\} .$

Xem đáp án

73. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{1}{\sin (x - \frac{π}{2})} .$

$D = ℝ \ \{k \frac{π}{2}, k \in ℤ\} .$

$D = ℝ \ \{k π, k \in ℤ\} .$

$D = ℝ \ \{(1 + 2 k) \frac{π}{2}, k \in ℤ\} .$

$D = ℝ \ \{(1 + 2 k) π, k \in ℤ\} .$

Xem đáp án

74. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{1}{\sin x - \cos x} .$

$D = ℝ .$

$D = ℝ \ \{- \frac{π}{4} + k π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{4} + k 2 π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{4} + k π, k \in ℤ\} .$

Xem đáp án

75. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \tan x + \cot x + \frac{1}{\sin x} + \frac{1}{\cos x}$ không xác định trong khoảng nào trong các khoảng sau đây?

$(k 2 π; \frac{π}{2} + k 2 π)$ với $k \in ℤ .$

$(π + k 2 π; \frac{3 π}{2} + k 2 π)$ với $k \in ℤ .$

$(\frac{π}{2} + k 2 π; π + k 2 π)$ với $k \in ℤ .$

$(π + k 2 π; 2 π + k 2 π)$ với $k \in ℤ .$

Xem đáp án

76. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \cot (2 x - \frac{π}{4}) + \sin 2 x .$

$D = ℝ \ \{\frac{π}{4} + k π, k \in ℤ\} .$

$D = \emptyset .$

$D = ℝ \ \{\frac{π}{8} + k \frac{π}{2}, k \in ℤ\} .$

$D = ℝ .$

Xem đáp án

77. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = 3 \tan^{2} (\frac{x}{2} - \frac{π}{4}) .$

$D = ℝ \ \{\frac{3 π}{2} + k 2 π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .$

$D = ℝ \ \{\frac{3 π}{2} + k π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

Xem đáp án

78. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \frac{\cos 2 x}{1 + \tan x}$ không xác định trong khoảng nào trong các khoảng sau đây?

$(\frac{π}{2} + k 2 π; \frac{3 π}{4} + k 2 π)$ với $k \in ℤ .$

$(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ với $k \in ℤ .$

$(\frac{3 π}{4} + k 2 π; \frac{3 π}{2} + k 2 π)$ với $k \in ℤ .$

$(π + k 2 π; \frac{3 π}{2} + k 2 π)$ với $k \in ℤ .$

Xem đáp án

79. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \frac{3 \tan x - 5}{1 - \sin^{2} x} .$

$D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

$D = ℝ \ \{π + k π, k \in ℤ\} .$

$\cos x \neq \pm 1 \Leftrightarrow \sin x \neq 0 \Leftrightarrow x \neq k π, k \in ℤ .$

Xem đáp án

80. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \sqrt{\sin x + 2} .$

$D = ℝ .$

$D = [- 2; + \infty) .$

$D = [0; 2 π] .$

$D = \emptyset .$

Xem đáp án

81. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \sqrt{\sin x - 2} .$

$D = ℝ .$

$ℝ \ \{k π, k \in ℤ\} .$

$D = [- 1; 1] .$

$D = \emptyset .$

Xem đáp án

82. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định $D$ của hàm số $y = \frac{1}{\sqrt{1 - \sin x}} .$

$D = ℝ \ \{k π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

$D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .$

$D = \emptyset .$

Xem đáp án

83. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \sqrt{1 - \sin 2 x} - \sqrt{1 + \sin 2 x} .$

$D = \emptyset .$

$D = ℝ .$

$D = [\frac{π}{6} + k 2 π; \frac{5 π}{6} + k 2 π], k \in ℤ .$

$D = [\frac{5 π}{6} + k 2 π; \frac{13 π}{6} + k 2 π], k \in ℤ .$

Xem đáp án

84. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \sqrt{5 + 2 \cot^{2} x - \sin x} + \cot (\frac{π}{2} + x) .$

$D = ℝ \ \{\frac{k π}{2}, k \in ℤ\} .$

$D = ℝ \ \{- \frac{π}{2} + k π, k \in ℤ\} .$

$D = ℝ .$

$D = ℝ \ \{k π, k \in ℤ\} .$

Xem đáp án

85. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập xác định D của hàm số $y = \tan (\frac{π}{2} \cos x) .$

$D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}$ .

$D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

$D = ℝ$ .

$D = ℝ \ \{k π, k \in ℤ\}$ .

Xem đáp án

86. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = \sin x .$

$y = \cos x .$

$y = \tan x .$

$y = \cot x .$

Xem đáp án

87. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = - \sin x .$

$y = \cos x - \sin x .$

$y = \cos x + \sin^{2} x .$

$y = \cos x \sin x .$

Xem đáp án

88. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = \sin 2 x .$

$y = x \cos x .$

$y = \cos x . \cot x .$

$y = \frac{\tan x}{\sin x} .$

Xem đáp án

89. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = |\sin x| .$

$y = x^{2} \sin x .$

$y = \frac{x}{\cos x} .$

$y = x + \sin x .$

Xem đáp án

90. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?

$y = \sin x \cos 2 x .$

$y = \sin^{3} x . \cos (x - \frac{π}{2}) .$

$y = \frac{\tan x}{\tan^{2} x + 1} .$

$y = \cos x \sin^{3} x .$

Xem đáp án

91. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số lẻ?

y = cosx + sin²x.

y = sinx + cosx.

y = ‒cosx.

y = sinxcos3x.

Xem đáp án

92. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

$y = \cot 4 x .$

$y = \frac{\sin x + 1}{\cos x} .$

$y = \tan^{2} x .$

$y = |\cot x| .$

Xem đáp án

93. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số lẻ?

$y = \sin (\frac{π}{2} - x) .$

$y = \sin^{2} x .$

$y = \frac{\cot x}{\cos x} .$

$y = \frac{\tan x}{\sin x} .$

Xem đáp án

94. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số lẻ?

$y = 1 - \sin^{2} x .$

$y = |\cot x| . \sin^{2} x .$

$y = x^{2} \tan 2 x - \cot x .$

$y = 1 + |\cot x + \tan x| .$

Xem đáp án

95. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (x) = \sin 2 x$ và $g (x) = \tan^{2} x .$ Chọn mệnh đề đúng

$f (x)$ là hàm số chẵn, $g (x)$ là hàm số lẻ.

$f (x)$ là hàm số lẻ, $g (x)$ là hàm số chẵn.

$f (x)$ là hàm số chẵn, $g (x)$ là hàm số chẵn.

$f (x)$ và $g (x)$ đều là hàm số lẻ.

Xem đáp án

96. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai hàm số $f (x) = \frac{\cos 2 x}{1 + \sin^{2} 3 x}$ và $g (x) = \frac{|\sin 2 x| - \cos 3 x}{2 + \tan^{2} x}$ . Mệnh đề nào sau đây là đúng?

$f (x)$ lẻ và $g (x)$ chẵn.

$f (x)$ và $g (x)$ chẵn.

$f (x)$ chẵn, $g (x)$ lẻ.

$f (x)$ và $g (x)$ lẻ.

Xem đáp án

97. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

$y = \frac{1}{\sin^{3} x} .$

$y = \sin (x + \frac{π}{4}) .$

$y = \sqrt{2} \cos (x - \frac{π}{4}) .$

$y = \sqrt{\sin 2 x} .$

Xem đáp án

98. Trắc nghiệm

• 1 điểm • Không giới hạn

Mệnh đề nào sau đây là sai?

Đồ thị hàm số $y = |\sin x|$ đối xứng qua gốc tọa độ O

Đồ thị hàm số $y = \cos x$ đối xứng qua trục Oy

Đồ thị hàm số $y = |\tan x|$ đối xứng qua trục Oy.

Đồ thị hàm số $y = \tan x$ đối xứng qua gốc tọa độ O

Xem đáp án

99. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số chẵn?

$y = 2 \cos (x + \frac{π}{2}) + \sin (π - 2 x) .$

$y = \sin (x - \frac{π}{4}) + \sin (x + \frac{π}{4}) .$

$y = \sqrt{2} \sin (x + \frac{π}{4}) - \sin x .$

$y = \sqrt{\sin x} + \sqrt{\cos x} .$

Xem đáp án

100. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào là hàm số lẻ ?

$y = x^{4} + \cos (x - \frac{π}{3}) .$

$y = x^{2017} + \cos (x - \frac{π}{2}) .$

$y = 2015 + \cos x + \sin^{2018} x .$

$y = \tan^{2017} x + \sin^{2018} x .$

Xem đáp án

101. Trắc nghiệm

• 1 điểm • Không giới hạn

Mệnh đề nào sau đây là sai?

Hàm số $y = \sin x$ tuần hoàn với chu kì $2 π .$

Hàm số $y = \cos x$ tuần hoàn với chu kì $2 π .$

Hàm số $y = \tan x$ tuần hoàn với chu kì $2 π .$

Hàm số $y = \cot x$ tuần hoàn với chu kì $π .$

Xem đáp án

102. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

$y = \sin x$

$y = x + \sin x$

$y = x \cos x .$

$y = \frac{\sin x}{x} .$

Xem đáp án

103. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau đây, hàm số nào không tuần hoàn?

$y = \cos x .$

$y = \cos 2 x .$

$y = x^{2} \cos x$

$y = \frac{1}{\sin 2 x} .$

Xem đáp án

104. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \sin (5 x - \frac{π}{4}) .$

$T = \frac{2 π}{5} .$

$T = \frac{5 π}{2} .$

$T = \frac{π}{2} .$

$T = \frac{π}{8} .$

Xem đáp án

105. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \cos (\frac{x}{2} + 2016) .$

$T = 4 π .$

$T = 2 π .$

$T = - 2 π .$

$T = π .$

Xem đáp án

106. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = - \frac{1}{2} \sin (100 π x + 50 π) .$

$T = \frac{1}{50} .$

$T = \frac{1}{100} .$

$T = \frac{π}{50} .$

$T = 200 π^{2} .$

Xem đáp án

107. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \cos 2 x + \sin \frac{x}{2} .$

$T = 4 π .$

$T = π .$

$T = \frac{π}{2} .$

Xem đáp án

108. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \cos 3 x + \cos 5 x .$

$T = π .$

$T = 3 π .$

$T = 2 π .$

$T = 5 π .$

Xem đáp án

109. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = 3 \cos (2 x + 1) - 2 \sin (\frac{x}{2} - 3) .$

$T = 2 π .$

$T = 4 π$

$T = 6 π$

$T = π .$

Xem đáp án

110. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \sin (2 x + \frac{π}{3}) + 2 \cos (3 x - \frac{π}{4}) .$

$T = 2 π .$

$T = π .$

$T = 3 π .$

$T = 4 π .$

Xem đáp án

111. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \tan 3 π x .$

$T = \frac{π}{3} .$

$T = \frac{4}{3} .$

$T = \frac{2 π}{3} .$

$T = \frac{1}{3} .$

Xem đáp án

112. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \tan 3 x + \cot x .$

$T = 4 π .$

$T = π .$

$T = 3 π .$

$T = \frac{π}{3} .$

Xem đáp án

113. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \cot \frac{x}{3} + \sin 2 x .$

$T = 4 π .$

$T = π .$

$T = 3 π .$

$T = \frac{π}{3} .$

Xem đáp án

114. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \sin \frac{x}{2} - \tan (2 x + \frac{π}{4}) .$

$T = 4 π .$

$T = π .$

$T = 3 π .$

$T = 2 π .$

Xem đáp án

115. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = 2 \cos^{2} x + 2017.$

$T = 3 π .$

$T = 2 π .$

$T = π .$

$T = 4 π .$

Xem đáp án

116. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = 2 \sin^{2} x + 3 \cos^{2} 3 x .$

$T = π .$

$T = 2 π .$

$T = 3 π .$

$T = \frac{π}{3} .$

Xem đáp án

117. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm chu kì T của hàm số $y = \tan 3 x - \cos^{2} 2 x .$

$T = π .$

$T = \frac{π}{3} .$

$T = \frac{π}{2} .$

$T = 2 π .$

Xem đáp án

118. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây có chu kì khác $π$ ?

$y = \sin (\frac{π}{3} - 2 x) .$

$y = \cos 2 (x + \frac{π}{4}) .$

$y = \tan (- 2 x + 1) .$

$y = \cos x \sin x .$

Xem đáp án

119. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số nào sau đây có chu kì khác $2 π$ ?

$y = \cos^{3} x .$

$y = \sin \frac{x}{2} \cos \frac{x}{2} .$

$y = \sin^{2} (x + 2) .$

$y = \cos^{2} (\frac{x}{2} + 1) .$

Xem đáp án

120. Trắc nghiệm

• 1 điểm • Không giới hạn

Hai hàm số nào sau đây có chu kì khác nhau?

$y = \cos x$ và $y = \cot \frac{x}{2} .$

$y = \sin x$ và $y = \tan 2 x .$

$y = \sin \frac{x}{2}$ và $y = \cos \frac{x}{2} .$

$y = \tan 2 x$ và $y = \cot 2 x .$

Xem đáp án

121. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \sin x$ . Mệnh đề nào sau đây là đúng?

Hàm số đồng biến trên khoảng $(\frac{π}{2}; π)$ , nghịch biến trên khoảng $(π; \frac{3 π}{2})$ .

Hàm số đồng biến trên khoảng $(- \frac{3 π}{2}; - \frac{π}{2})$ , nghịch biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ .

Hàm số đồng biến trên khoảng $(0; \frac{π}{2})$ , nghịch biến trên khoảng $(- \frac{π}{2}; 0)$ .

Hàm số đồng biến trên khoảng $(- \frac{π}{2}; \frac{π}{2})$ , nghịch biến trên khoảng $(\frac{π}{2}; \frac{3 π}{2})$ .

Xem đáp án

122. Trắc nghiệm

• 1 điểm • Không giới hạn

Với $x \in (\frac{31 π}{4}; \frac{33 π}{4})$ , mệnh đề nào sau đây là đúng?

Hàm số $y = \cot x$ nghịch biến.

Hàm số $y = \tan x$ nghịch biến.

Hàm số $y = \sin x$ đồng biến.

Hàm số $y = \cos x$ nghịch biến.

Xem đáp án

123. Trắc nghiệm

• 1 điểm • Không giới hạn

Với $x \in (0; \frac{π}{4})$ , mệnh đề nào sau đây là đúng?

Cả hai hàm số $y = - \sin 2 x$ và $y = - 1 + \cos 2 x$ đều nghịch biến.

Cả hai hàm số $y = - \sin 2 x$ và $y = - 1 + \cos 2 x$ đều đồng biến.

Hàm số $y = - \sin 2 x$ nghịch biến, hàm số $y = - 1 + \cos 2 x$ đồng biến.

Hàm số $y = - \sin 2 x$ đồng biến, hàm số $y = - 1 + \cos 2 x$ nghịch biến.

Xem đáp án

124. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \sin 2 x$ đồng biến trên khoảng nào trong các khoảng sau?

$(0; \frac{π}{4})$ .

$(\frac{π}{2}; π)$ .

$(π; \frac{3 π}{2})$ .

$(\frac{3 π}{2}; 2 π)$ .

Xem đáp án

125. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau, hàm số nào đồng biến trên khoảng $(- \frac{π}{3}; \frac{π}{6})$ ?

$y = \tan (2 x + \frac{π}{6})$ .

$y = \cot (2 x + \frac{π}{6})$ .

$y = \sin (2 x + \frac{π}{6})$ .

$y = \cos (2 x + \frac{π}{6})$ .

Xem đáp án

126. Trắc nghiệm

• 1 điểm • Không giới hạn

Đồ thị hàm số $y = \cos (x - \frac{π}{2})$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x$ bằng cách:

Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2} .$

Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2} .$

Tịnh tiến $(C)$ lên trên một đoạn có độ dài là $\frac{π}{2} .$

Tịnh tiến $(C)$ xuống dưới một đoạn có độ dài là $\frac{π}{2} .$

Xem đáp án

127. Trắc nghiệm

• 1 điểm • Không giới hạn

Đồ thị hàm số $y = \sin x$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x$ bằng cách:

Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2} .$

Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2} .$

Tịnh tiến $(C)$ lên trên một đoạn có độ dài là $\frac{π}{2} .$

Tịnh tiến $(C)$ xuống dưới một đoạn có độ dài là $\frac{π}{2} .$

Xem đáp án

128. Trắc nghiệm

• 1 điểm • Không giới hạn

Đồ thị hàm số $y = \sin x$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x + 1$ bằng cách:

Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1đơn vị.

Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1đơn vị.

Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1đơn vị.

Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1đơn vị.

Xem đáp án

129. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

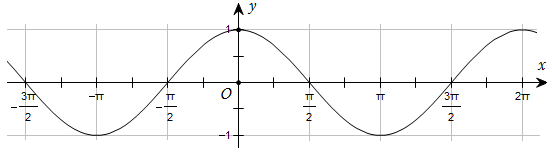
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = 1 + \sin 2 x .$

$y = \cos x .$

$y = - \sin x .$

$y = - \cos x .$

Xem đáp án

130. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

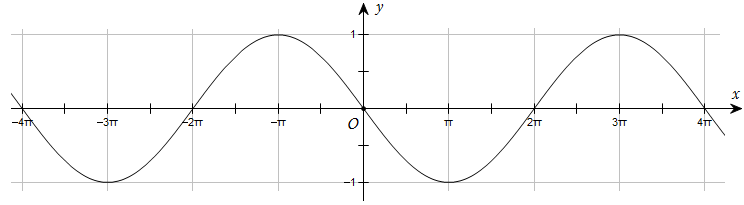
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \sin \frac{x}{2} .$

$y = \cos \frac{x}{2} .$

$y = - \cos \frac{x}{4} .$

$y = \sin (- \frac{x}{2}) .$

Xem đáp án

131. Trắc nghiệm

• 1 điểm • Không giới hạn

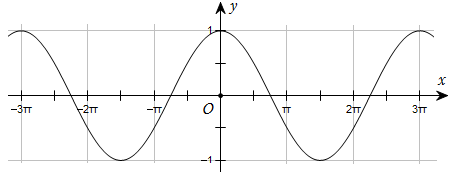
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \cos \frac{2 x}{3} .$

$y = \sin \frac{2 x}{3} .$

$y = \cos \frac{3 x}{2} .$

$y = \sin \frac{3 x}{2} .$

Xem đáp án

132. Trắc nghiệm

• 1 điểm • Không giới hạn

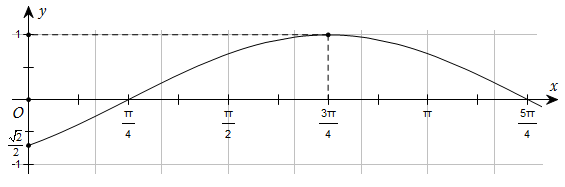
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C,D Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \sin (x - \frac{π}{4}) .$

$y = \cos (x + \frac{3 π}{4}) .$

$y = \sqrt{2} \sin (x + \frac{π}{4}) .$

$y = \cos (x - \frac{π}{4}) .$

Xem đáp án

133. Trắc nghiệm

• 1 điểm • Không giới hạn

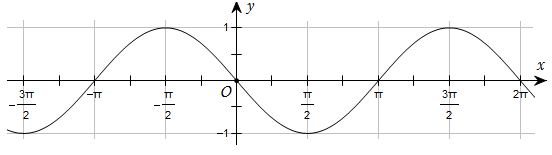
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Media VietJack Hỏi hàm số đó là hàm số nào?

$y = \sin (x - \frac{π}{4}) .$

$y = \cos (x - \frac{π}{4}) .$

$y = \sqrt{2} \sin (x + \frac{π}{4}) .$

$y = \sqrt{2} \cos (x + \frac{π}{4}) .$

Xem đáp án

134. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

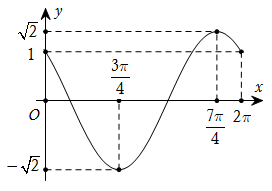Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \sin x .$

$y = |\sin x| .$

$y = \sin |x| .$

$y = - \sin x .$

Xem đáp án

135. Trắc nghiệm

• 1 điểm • Không giới hạn

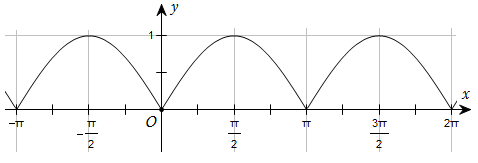
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \cos x .$

$y = - \cos x$

$y = \cos |x| .$

$y = |\cos x| .$

Xem đáp án

136. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

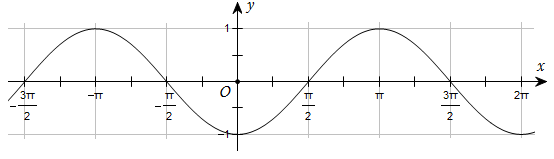
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = |\sin x| .$

$y = \sin |x| .$

$y = \cos |x| .$

$y = |\cos x| .$

Xem đáp án

137. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

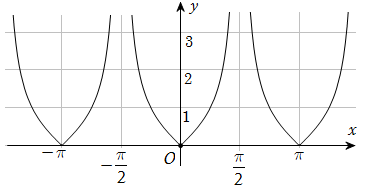
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \tan x .$

$y = \cot x .$

$y = |\tan x| .$

$y = |\cot x| .$

Xem đáp án

138. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

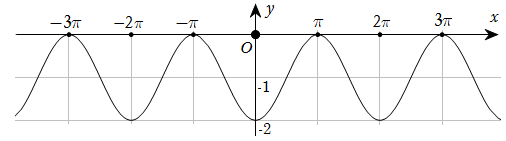
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = \sin (x - \frac{π}{2}) - 1.$

$y = 2 \sin (x - \frac{π}{2}) .$

$y = - \sin (x - \frac{π}{2}) - 1.$

$y = \sin (x + \frac{π}{2}) + 1.$

Xem đáp án

139. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

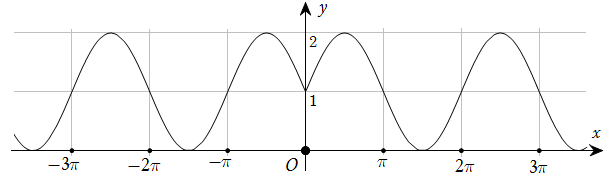
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = 1 + \sin |x| .$

$y = |\sin x|$ .

$y = 1 + |\cos x|$

$y = 1 + |\sin x|$

Xem đáp án

140. Trắc nghiệm

• 1 điểm • Không giới hạn

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

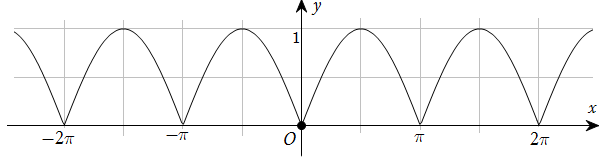
Media VietJack

Hỏi hàm số đó là hàm số nào?

$y = 1 + \sin |x| .$

$y = |\sin x|$ .

$y = 1 + |\cos x|$ .

$y = 1 + |\sin x|$ .

Xem đáp án

141. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = 3 \sin x - 2.$

$M = 1, m = - 5.$

$M = 3, m = 1.$

$M = 2, m = - 2.$

$M = 0, m = - 2.$

Xem đáp án

142. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập giá trị T của hàm số $y = 3 \cos 2 x + 5.$

$T = [- 1; 1] .$

$T = [- 1; 11] .$

$T = [2; 8] .$

$T = [5; 8] .$

Xem đáp án

143. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập giá trị T của hàm số $y = 5 - 3 \sin x .$

$T = [- 1; 1] .$

$T = [- 3; 3] .$

$T = [2; 8] .$

$T = [5; 8] .$

Xem đáp án

144. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = - 2 \sin (x + \frac{π}{3}) + 2$ . Mệnh đề nào sau đây là đúng?

$y \geq - 4, \forall x \in ℝ .$

$y \geq 4, \forall x \in ℝ .$

$y \geq 0, \forall x \in ℝ .$

$y \geq 2, \forall x \in ℝ .$

Xem đáp án

145. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = 5 + 4 \sin 2 x \cos 2 x$ có tất cả bao nhiêu giá trị nguyên?

Xem đáp án

146. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị nhỏ nhất m của hàm số $y = - \sqrt{2} \sin (2016 x + 2017)$ .

$m = - 2016 \sqrt{2} .$

$m = - \sqrt{2} .$

$m = - 1.$

$m = - 2017 \sqrt{2} .$

Xem đáp án

147. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị nhỏ nhất m của hàm số $y = \frac{1}{\cos x + 1} .$

$m = \frac{1}{2} .$

$m = \frac{1}{\sqrt{2}} .$

$m = 1.$

$m = \sqrt{2} .$

Xem đáp án

148. Trắc nghiệm

• 1 điểm • Không giới hạn

Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x + \cos x$ . Tính $P = M - m .$

$P = 4.$

$P = 2 \sqrt{2} .$

$P = \sqrt{2} .$

$P = 2.$

Xem đáp án

149. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập giá trị T của hàm số $y = \sin 2017 x - \cos 2017 x .$

$T = [- 2; 2] .$

$T = [- 4034; 4034] .$

$T = [- \sqrt{2}; \sqrt{2}] .$

$T = [0; \sqrt{2}] .$

Xem đáp án

150. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \sin (x + \frac{π}{3}) - \sin x$ có tất cả bao nhiêu giá trị nguyên?

Xem đáp án

151. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \sin^{4} x - \cos^{4} x$ đạt giá trị nhỏ nhất tại $x = x_{0}$ . Mệnh đề nào sau đây là đúng?

$x_{0} = k 2 π, k \in ℤ .$

$x_{0} = k π, k \in ℤ .$

$x_{0} = π + k 2 π, k \in ℤ .$

$x_{0} = \frac{π}{2} + k π, k \in ℤ .$

Xem đáp án

152. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = 1 - 2 |\cos 3 x| .$

$M = 3, m = - 1.$

$M = 1, m = - 1.$

$M = 2, m = - 2.$

$M = 0, m = - 2.$

Xem đáp án

153. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M của hàm số $y = 4 \sin^{2} x + \sqrt{2} \sin (2 x + \frac{π}{4}) .$

$M = \sqrt{2} .$

$M = \sqrt{2} - 1.$

$M = \sqrt{2} + 1.$

$M = \sqrt{2} + 2.$

Xem đáp án

154. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập giá trị T của hàm số $y = \sin^{6} x + \cos^{6} x .$

$T = [0; 2] .$

$T = [\frac{1}{2}; 1] .$

$T = [\frac{1}{4}; 1] .$

$T = [0; \frac{1}{4}] .$

Xem đáp án

155. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = \cos^{4} x + \sin^{4} x$ . Mệnh đề nào sau đây là đúng?

$y \leq 2, \forall x \in ℝ .$

$y \leq 1, \forall x \in ℝ .$

$y \leq \sqrt{2}, \forall x \in ℝ .$

$y \leq \frac{\sqrt{2}}{2}, \forall x \in ℝ .$

Xem đáp án

156. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = 1 + 2 \cos^{2} x$ đạt giá trị nhỏ nhất tại $x = x_{0}$ . Mệnh đề nào sau đây là đúng?

$x_{0} = π + k 2 π, k \in ℤ .$

$x_{0} = \frac{π}{2} + k π, k \in ℤ .$

$x_{0} = k 2 π, k \in ℤ .$

$x_{0} = k π, k \in ℤ .$

Xem đáp án

157. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số $y = \sin^{2} x + 2 \cos^{2} x .$

$M = 3, m = 0.$

$M = 2, m = 0.$

$M = 2, m = 1.$

$M = 3, m = 1.$

Xem đáp án

158. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M của hàm số $y = \frac{2}{1 + \tan^{2} x} .$

$M = \frac{1}{2} .$

$M = \frac{2}{3} .$

$M = 1.$

$M = 2.$

Xem đáp án

159. Trắc nghiệm

• 1 điểm • Không giới hạn

Gọi m,M lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 8 \sin^{2} x + 3 \cos 2 x$ . Tính $P = 2 M - m^{2} .$

$P = 1.$

$P = 2.$

$P = 112.$

$P = 130.$

Xem đáp án

160. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị nhỏ nhất m của hàm số $y = 2 \sin^{2} x + \sqrt{3} \sin 2 x$ .

$m = 2 - \sqrt{3} .$

$m = - 1.$

$m = 1.$

$m = - \sqrt{3} .$

Xem đáp án

161. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm tập giá trị T của hàm số $y = 12 \sin x - 5 \cos x .$

$T = [- 1; 1] .$

$T = [- 7; 7] .$

$T = [- 13; 13] .$

$T = [- 17; 17] .$

Xem đáp án

162. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M của hàm số $y = 4 \sin 2 x - 3 \cos 2 x .$

$M = 3.$

$M = 1.$

$M = 5.$

$M = 4.$

Xem đáp án

163. Trắc nghiệm

• 1 điểm • Không giới hạn

Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin^{2} x - 4 \sin x + 5$ . Tính $P = M - 2 m^{2} .$

$P = 1.$

$P = 7.$

$P = 8.$

$P = 2.$

Xem đáp án

164. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \cos^{2} x - \cos x$ có tất cả bao nhiêu giá trị nguyên?

Xem đáp án

165. Trắc nghiệm

• 1 điểm • Không giới hạn

Hàm số $y = \cos^{2} x + 2 \sin x + 2$ đạt giá trị nhỏ nhất tại $x_{0}$ . Mệnh đề nào sau đây là đúng?

$x_{0} = \frac{π}{2} + k 2 π, k \in ℤ .$

$x_{0} = - \frac{π}{2} + k 2 π, k \in ℤ .$

$x_{0} = π + k 2 π, k \in ℤ .$

$x_{0} = k 2 π, k \in ℤ .$

Xem đáp án

166. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M và nhất m của hàm số $y = \sin^{4} x - 2 \cos^{2} x + 1$

$M = 2, m = - 2.$

$M = 1, m = 0.$

$M = 4, m = - 1.$

$M = 2, m = - 1.$

Xem đáp án

167. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị nhỏ nhất m của hàm số $y = 4 \sin^{4} x - \cos 4 x$ .

$m = - 3.$

$m = - 1.$

$m = 3.$

$m = - 5.$

Xem đáp án

168. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y = \sqrt{7 - 3 \cos^{2} x} .$

$M = \sqrt{10}, m = 2.$

$M = \sqrt{7}, m = 2.$

$M = \sqrt{10}, m = \sqrt{7} .$

$M = 0, m = 1.$

Xem đáp án

169. Trắc nghiệm

• 1 điểm • Không giới hạn

Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số $y = 4 \sin [\frac{π}{178} (t - 60)] + 10$ với $t \in ℤ$ và $0 < t \leq 365$ . Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?

28 tháng 5.

29 tháng 5.

30 tháng 5.

31 tháng 5

Xem đáp án

170. Trắc nghiệm

• 1 điểm • Không giới hạn

Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức $h = 3 \cos (\frac{π t}{8} + \frac{π}{4}) + 12.$ Mực nước của kênh cao nhất khi: