177 câu hỏi
Tìm tất cả giá trị của a để tập giá trị của hàm số chứa đoạn .
Hàm số có tập xác định , hàm số có tập xác định . Khi đó số phần tử của tập là:
4
5
6
7
Cho hàm số xác địnhvới mọi khi .
Giá trị
2
3
4
5
Cho . Biết rằng luôn cắt đường phân giác góc phần tư thứ nhất tại hai điểm A,B. Gọi lần lượt là hình chiếu của A, B lên Ox, lần lượt là hình chiếu của A, B lên Oy. Có bao nhiêu giá trị của m khác 0, -1 để tam giác có diện tích gấp 4 lần diện tích tam giác
1
4
2
3
Tìm tất cả các giá trị nguyên của tham số m để hàm số sau có tập xác định là R
2
3
4
5
Cho hàm số , m là tham số. Có bao nhiêu giá trị nguyên m để hàm số đã cho xác định trên đoạn ?
2
3
1
vô số
Tìm m để các hàm số xác định với mọi thuộc khoảng .
Tìm m để hàm số xác định trên khoảng .
Cho hàm số ( m là tham số). Để tập xác định của hàm số chỉ có đúng một phần tử thì với tối giản. Tính a+b.
3025
Cho hàm số . Có bao nhiêu giá trị của tham số m để hàm số xác định trên đoạn .
1
2
3
4
Tìm m để hàm số xác định trên khoảng .
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số xác định trên ?
6
7
8
9
Gọi S là tập tất cả các giá trị nguyên dương của m sao cho hàm số xác định trên . Khi đó số các phần tử của S là.
0
2
4
5
Cho hàm số có đồ thị như hình vẽ. Giá trị nguyên lớn nhất của để hàm số có TXĐ là R .
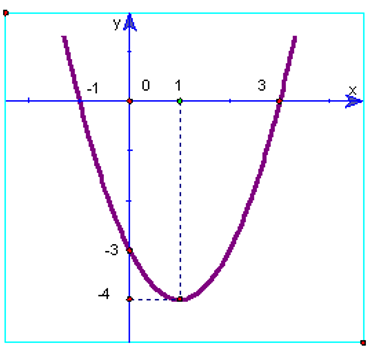
Tìm số giá trị nguyên của để hàm số xác định .
2018
2019
2020
Tìm m để hàm số xác định .
Cho hàm sô . Gọi S là tập hợp các giá trị nguyên của để hàm số xác định trên R. Hỏi tập S có bao nhiêu phần tử?
2018
2019
2020
2021
Cho hàm số . Có bao nhiêu giá trị của tham số m để hàm số xác định trên đoạn .
1
2
3
4
Cho hàm số . Tìm tất cả các giá trị của tham số m để hàm số có tập xác định là tập số thực R
Có bao nhiêu giá trị nguyên của tham số m trên đoạn để hàm số xác định trên .
2018
2019
4036
4037
Tìm số giá trị k nguyên để hàm số xác định trên khoảng .
1
2
3
4
Cho hàm số có đồ thị sau
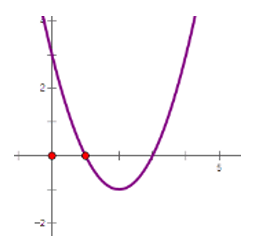
Có bao nhiêu giá trị nguyên của m để có bốn nghiệm phân biệt.
2
3
4
5
Cho hàm số có đồ thị là đường cong trong hình vẽ dưới đây
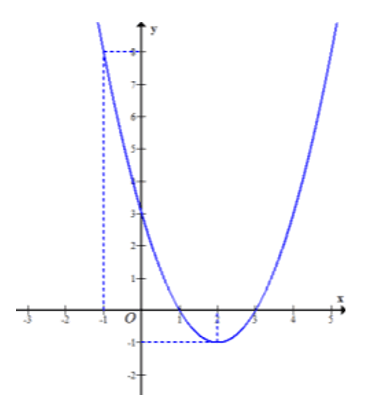
Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình có nghiệm phân biệt thuộc đoạn . Số phần tử của S là
7
8
3
4
Cho hàm số có đồ thị như hình vẽ bên. Gọi là tập hợp tất cả các giá trị của tham số m để phương trình có bốn nghiệm phân biệt . Tình .
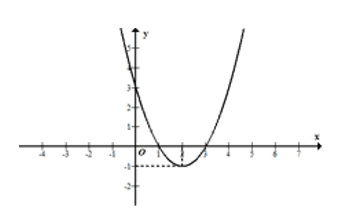
8000
1600
16000
800
Cho hàm số có đồ thị (như hình vẽ). Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm phân biệt?
Cho hàm số có đồ thị (C). Giả sử thuộc sao (C) cho khoảng cách từ điểm M tới đường thẳng là nhỏ nhất. Tính .
4
6
5
7
Cho parabol , biết (P) đi qua điểm A(1;5) và các điểm cố định của họ parabol . Tính tổng .
1
2
6
4
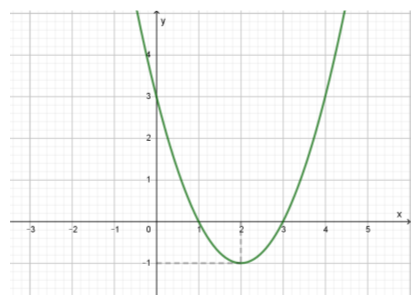
Hàm số có đồ thị như hình vẽ.
Khi đó bằng
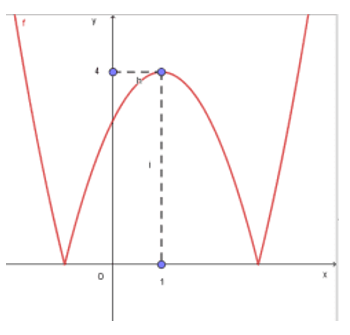
Cho hàm số có tập xác định là R và đồ thị như hình vẽ
.
Biểu thức nhận giá trị dương trên
Cho hai parabol: . Có bao nhiêu cặp số (m;n) để hai parabol trên không có cùng trục đối xứng nhưng đi qua đỉnh của nhau?
0
1
2
3
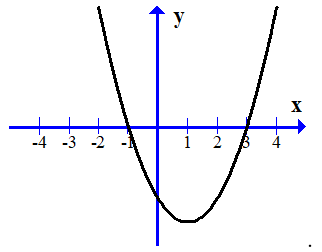
Cho đồ thị hàm số (hình vẽ bên).
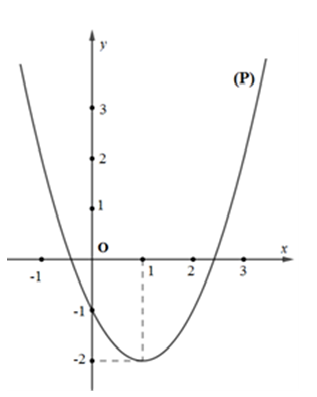
Dựa vào đồ thị (P) xác định số giá trị nguyên dương của m để phương trình có nghiệm
0
1
2
3
Cho hai đường thẳng và . Gọi S là tập hợp các giá trị nguyên dương của m để tam giác tạo thành bởi và trục hoành có diện tích lớn hơn hoặc bằng 8 . Tính tổng các phần tử của tập S.
1
2
3
4
Gọi là tập hợp các điểm thỏa mãn hệ thức , trục chia hình thành hai phần có diện tích trong đó là phần diện tích nằm phía trên trục hoành. Tỉ số là:
Cho hàm số có đồ thị như hình vẽ.
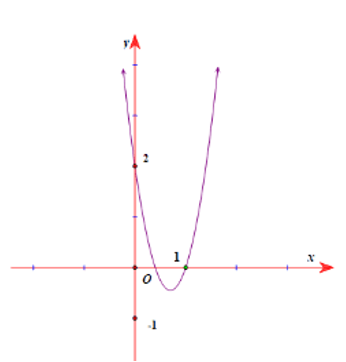
Số nghiệm thực của phương trình là?
0
2
3
4
Tính tổng bình phương các giá trị m của để phương trình có nghiệm duy nhất.
P=5
Cho hàm số có đồ thị sau
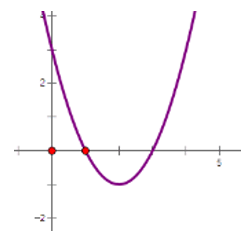
Có bao nhiêu giá trị nguyên của m để có bốn nghiệm phân biệt.
2
3
4
5
Cho phương trình . Giá trị m để phương trình có bốn nghiệm
2
1
3
4
Cho hàm số có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt?
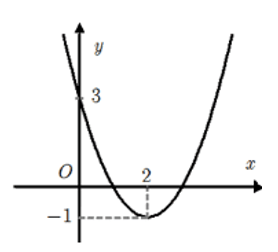
Cho Parabol (P): có đỉnh I.
Biết (P) cắt Ox tại hai điểm phân biệt A, B và tam giác ABI vuông cân. Khi đó đẳng thức nào sau đây đúng?
Biết đồ thị hàm số bậc hai có điểm chung duy nhất với và cắt đường thẳng tại hai điểm có hoành độ lần lượt -1 là và 5. Tính
1
0
-1
-2
Cho parabol : , biết:
đi qua cắt Ox tại và Q sao cho có diện tích bằng 1 biết hoành độ điểm nhỏ hơn 3 với I là đinh của (P). Tính
1
-2
0
-1
Cho đồ thị hàm số (P): trong đó x là ẩn, m là tham số. Hỏi có bao nhiêu giá trị của sao cho khoảng cách từ gốc 0 của hệ trục tọa độ đến đỉnh của Parabol (P) bằng 5.
3
4
5
có vô số giá trị.
Cho hàm số có đồ thị và đường thẳng (m là tham số). Có bao nhiêu giá trị nguyên của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ là , thỏa mãn .
1
3
4
6
Cho hai hàm số bậc hai thỏa mãn ;. Biết rằng hai đồ thi hàm số cắt nhau tại hai điểm phân biệt là . Đường thẳng d vuông góc với AB tạo với hai trục tọa độ một tam giác có diện tích bằng 36. Hỏi điểm nào dưới đây thuộc đường thẳng d
M(-2;1)
N(-1;9)
P(1;4)
Q(3;5)
Biết rằng đường thẳng luôn cắt parabol tại hai điểm phân biệt A và B, khi đó quỹ tích trung điểm của đoạn thẳng AB là:
đường parabol .
đường parabol .
đường thẳng .
đường thẳng .
Cho hàm số có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt?
Cho đường thẳng đi qua điểm , cắt hai tia , và cách gốc tọa độ một khoảng bằng . Tính giá trị của biểu thức
Cho hàm số có đồ thị và đường thẳng . Gọi là tập tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại hai điểm phân biệt có hoành độ thỏa mãn . Tổng các phần tử của S là:
Cho hàm số có đồ thị là hình bên dưới. Đặt T là tổng các nghiệm của phương trình: . T thuộc tập hợp nào sau đây?
Cho parabol (P): và đường thẳng (d) đi qua gốc tọa độ và có hệ số góc là k . Gọi A và B là các giao điểm của (P) và (d). Giả sử A, B lần lượt có hoành độ là . Giá trị nhỏ nhất của biểu thức bằng:
1
2
3
4
Có bao nhiêu giá trị của m để phương trình có đúng 5 nghiệm phân biệt?
1
2
3
4
Cho hai đường thẳng và . Có bao nhiêu giá trị nguyên của m để tam giác tạo thành bởi và trục hoành có diện tích lớn hơn hoặc bằng ?
1
2
3
4
Cho parabol (P): và đường thẳng (d) đi qua điểm có hệ số góc là . Gọi A và B là các giao điểm của (P) và (d). Giả sử A, B lần lượt có hoành độ là . Số các giá trị nguyên của k thỏa mãn là là
1
2
0
Vô số
Cho đường thẳng và Parabol với . (d) cắt tại hai điểm phân biệt . Gọi a và b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của độ dài đoạn thẳng MN. Tính tổng .
Cho Parabol và đường thẳng ( m là tham số). Có bao nhiêu giá trị nguyên dương của m thì đường thẳng (d) cắt Parabol (P) tại hai điểm sao cho biểu thức đạt giá trị nhỏ nhất.
1
2
3
4
Trong mặt phẳng tọa độ Oxy, cho Parabol (P) có phương trình và hai đường thẳng (d): ; (d’): (với) . Đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt A, B; đường thẳng (d’) cắt Parabol (P) tại hai điểm phân biệt C, D (với hoành độ điểm A và D là số âm) sao cho diện tích hình thang ABCD gấp 9 lần diện tích tam giác OCD. Khi đó giá trị m thuộc khoảng?
Cho hàm số có đồ thị nhu hình vẽ.
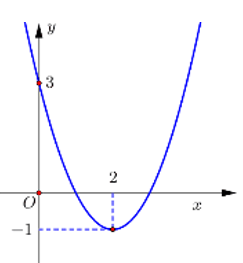
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình có 4 nghiệm phân biệt. Số phần tử của S là
1
2
3
4
Cho hàm số có đồ thị nhu hình vẽ.
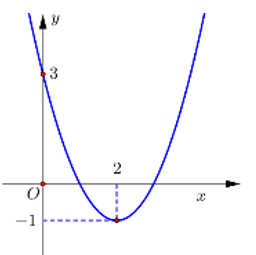
Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình có nghiệm phân biệt. Số phần tử của S là
1
2
3
4
Cho hàm số có đồ thị như hình vẽ.
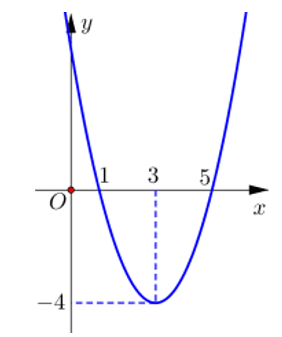
Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình có hai nghiệm. Tổng các phần tử của S bằng
-6
-4
4
-4
Gọi là tập hợp các giá trị thực của tham số sao cho parabol cắt tại hai điểm phân biệt thỏa mãn Tính tổng T các phần tử của S
Cho hàm số đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình có đúng 3 nghiệm phân biệt.
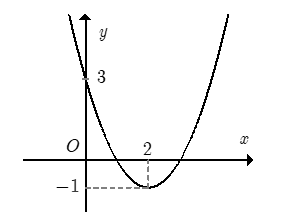
m=3
m=2
Cho hàm số biết đồ thị hàm số cắt trục tại hai điểm có hoành độ . Với giá trị nào của a thì biểu thức không phụ thuộc vào m.
Tìm tham số để đường thẳng cắt đồ thị của hàm số tại hai điểm A, B sao cho tam giác OAB vuông tại gốc tọa độ O.
1
2
3
4
Cho hàm số (m là tham số)
Có bao nhiêu giá trị nguyên của m để đồ thị hàm số cắt Ox tại 1 điểm thuộc khoảng (1;2).
0
1
2
3
Cho hàm số có đồ thị (P) và đường thẳng d: . Có bao nhiêu giá trị của tham số m để d cắt (P) tại hai điểm phân biệt A, B sao cho tam giác OAB có diện tích bằng .
2
1
0
3
Cho hai hàm số và . Tìm m để đồ thị các hàm số đó cắt nhau tại hai điểm A và B phân biệt sao cho nhỏ nhất (trong đó O là gốc tọa độ).
Không tồn tại m .
Cho hàm số bậc hai có đồ thị là và đường thẳng . Gọi S là tập gồm tất cả các giá trị thực của m sao cho (d) cắt (P) tại hai điểm phân biệt A và B thỏa mãn cho A, B nằm khác phía và cách đều đường thẳng . Mệnh đề nào sau đây là mệnh đề đúng?
Tổng của tất cả các phần tử của S là
Tổng của tất cả các phần tử của S là .
S có đúng một phần tử.
Cho đồ thị hàm số (P): và đường thẳng (d) trong đó x là ẩn, m là tham số. Hỏi có bao nhiêu giá trị nguyên của để (d) và (P) có điểm chung.
4037
4029
4035
4031
Cho Parabol (P): . Có bao nhiêu giá trị của tham số m để đồ thị (P) cắt trục Ox tại 2 điểm phân biệt A và B sao cho tam giác IAB là tam giác đều (Với I là đỉnh của (P)).
1
2
3
4
Parabol nhận ba đường thẳng làm các tiếp tuyến. Khi đó giá trị của là
-16
-25
-1
-25
Cho hàm số , ( m là tham số). Gọi giá trị của m để đồ thị hàm số (1) cắt trục hoành tại hai điểm phân biệt sao cho tam giác KAB vuông tại K , trong đó . Khi đó bằng:
13
12
11
10
Biết luôn đi qua 1 điểm cố định A, đường thẳng đi qua đi qua A và cắt tại điểm có tung độ bằng -2. Giả sử cắt (P) tại 2 điểm phân biệt A và B. Gọi là trung điểm của AB. Tổng các giá trị của m để (hoặc có thể cho) thỏa mãn bài toán thuộc khoảng nào sau đây:
Cho hàm số . Gọi S là tập hợp gồm tất cả các giá trị nguyên của tham số m để phương trình có 6 nghiệm phân biệt. Số phần tử của S là:
0
1
2
3
Cho parabol và đường thẳng (m là tham số). Gọi S là tập hợp các giá trị nguyên của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A,B thỏa mãn vuông tại O . Khi đó số các phần tử thuộc S bằng :
2
0
1
9
Cho hàm số có đồ thị là parabol đỉnh . Biết rằng đường thẳng cắt (P) tại hai điểm và tam giác đều. Tính .
Cho hai tập hợp , .
Giả sử các phần tử của A được sơn xanh, các phần tử của B được sơn đỏ.Người ta xếp các phần tử của A và B lên một trục số.Tìm số giá trị nguyên của m để có 4 phần tử và 2 phần tử cùng màu không đứng kề nhau.
9
6
5
10
Cho các Parabol có các đỉnh lần lượt là . Gọi là giao điểm của và . Biết rằng 4 điểm tạo thành tứ giác lồi có diện tích bằng Tính diện tích S của tam giác với là đỉnh của Parabol
Trong hệ trục , cho parabol (P) : và đường thẳng d: (với m là tham số). Tổng của tất cả các giá trị m để cho đường thẳng d cắt (P) tại hai điểm phân biệt A và B sao cho OA vuông góc với OB là :
1
2
Cho hàm số có đồ thị là parabol . Biết rằng đường thẳng : cắt (P) tại một điểm duy nhất, đường thẳng : cắt tại hai điểm phân biệt có hoành độ lần lượt là -1 và -5 . Tính giá trị .
Cho hàm số . Tất cả các giá trị m để hàm số có giá trị nhỏ nhất bằng 1 trên đoạn thuộc tập hợp nào sau đây ?
Cho parabol và đường thẳng . Có tất cả bao nhiêu giá trị nguyên của tham số m để (d) cắt (P) tại hai điểm phân biệt A,B nằm về hai phía của đường thẳng có phương trình ?
3
4
5
6
Cho hàm số . Gọi S là tập hợp các giá trị thực của m để đồ thị hàm số đã cho cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là thỏa mãn:
(*). Khi đó tổng các phần tử của là:
3
Cho hàm số : (C). Giả sử m là giá trị để đồ thị hàm số (C) cắt trục Ox tại 2 điểm phân biệt có hoành độ sao cho . Hỏi m gần với giá trị nào sau đây nhất:
không tồn tại m
0,53
1
1,5
Cho hàm số có đồ thị (P) và đường thẳng d: . Tìm tất cả các giá trị của tham số m để d cắt (P) tại hai điểm phân biệt A, B sao cho tam giác OAB có diện tích bằng .
không tồn tại m
Cho hàm số có đồ thị . Gọi là tập hợp các giá trị nguyên dương của tham số m để cho đồ thị cắt trục hoành tại hai điểm phân biệt. Số phần tử của P là
5
4
8
9
Cho parabol và đường thẳng . Tìm tất cả các giá trị thực của m để d cắt (P) tại hai điểm phân biệt sao cho diện tích tam giác OBA bằng .
Cho hàm số có đồ thị như hình dưới. Tìm m để phương trình có 3 nghiệm phân biệt.
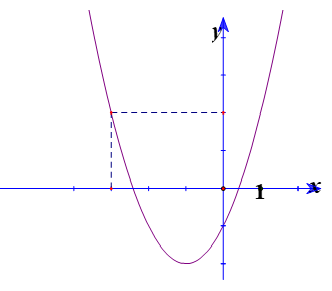
Cho hàm số có đồ thị và đường thẳng . Gọi S là tập tất cả các giá trị của tham số m để đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt có hoành độ thỏa mãn . Tổng các phần tử của S là:
Cho và hàm số xác định bởi . Biết đồ thị của hàm số cắt trục hoành và trục tung lần lượt tại A và B . Diện tích của tam giác (với là gốc tọa độ) bằng
Cho Parabol (P) : , đường thẳng đi qua và cắt Parabol đã cho tại hai điểm có hoành độ thỏa mãn phương trình , khi đó giá trị của tham số m thuộc khoảng nào sau đây?
Cho (P): cắt đường thẳng tại hai điểm phân biệt có hoành độ Xét hàm số , tính giá trị biểu thức
3
1
-3
0
Cho hàm số và hàm số , với m là tham số . Gọi m là giá trị sao cho đồ thị hai hàm số đã cho cắt nhau tại hai điểm phân biệt mà khoảng cách từ trung điểm K của đoạn thẳng EF đến trục hoành gấp đôi khoảng cách từ K đến trục tung. Khẳng định nào sau đây đúng?
Cho parabol ( m là tham sô). Gọi C là điểm thuộc (P) có hoành độ bằng -1 . Gọi S là tập tất cả các giá trị của m sao cho đường thẳng cắt tại hai điểm phân biệt thỏa tam giác vuông tại A . Tính tổng lập phương tất cả các phần tử của S .
1701
-1701
-1304
-1304
Cho Parabol và đường thẳng . Biết đường thẳng d cắt Parabol (P) tại hai điểm phân biệt thỏa mãn . Số giá trị nguyên dương của n bằng:
2
0
5
1
Cho (P). Có bao nhiêu giá trị nguyên của m để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ thõa mãn· .
1
2
3
0
Cho hàm số có đồ thị (P) và đường thẳng (d) có phương trình .Có bao nhiêu giá trị m nguyên để đường thẳng d cắt (P) tại hai điểm phân biệt.A, B sao cho .
8
6
7
2
Gọi là tập các giá trị của tham số m để phương trình có số nghiệm nhiều nhất. Tính
Biết rằng với giá trị của tham số m bằng , phân số tối giản) thì đường thẳng cắt parabol tại hai điểm phân biệt sao cho bé nhất. Khi đó giá trị là:
22
21
20
19
Cho hai hàm số và ( m là tham số) có đồ thị lần lượt là .Gọi S là tập hợp tất cả các giá trị của m để cắt nhau tại hai điểm có tổng các hoành độ là một số nguyên. Số tập con của S là:
3
4
8
lớn hơn 8
Cho hàm số có đồ thị (như hình vẽ). Hỏi có bao nhiêu giá trị nguyên của m để phương trình có đúng nghiệm phân biệt .
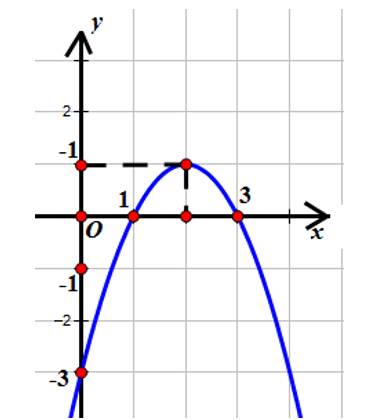
1
3
2
0
Cho parabol (p): và đường thẳng (d): .
Tính tổng các giá trị của m để đường thẳng (d) cắt (p) tại hai điểm phân biệt A và B sao cho ? Biết M (2; 9) ?
Cho hàm số bậc hai có đồ thị như hình vẽ dưới.
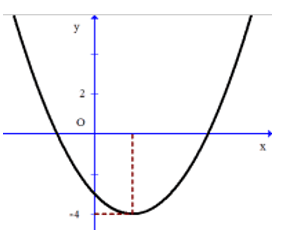
Tìm m để phương trình có 4 nghiệm thực phân biệt?
Tập các giá trị của m để phương trình có bốn nghiệm phân biệt là khoảng Tính
Cho parabol (P) có phương trình và đường thẳng d có phương trình . Tập nghiệm của bất phương trình là . Giả sử là giao điểm của và . Gọi với . Để diện tích đạt giá trị lớn nhất thì m phải thỏa mãn:
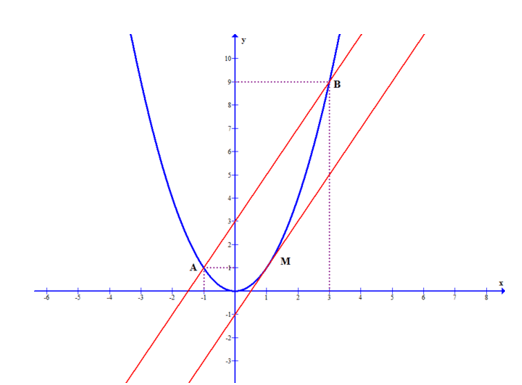
Tập hợp tất cả các giá trị của m để phương trình có ba nghiệm phân biệt thỏa mãn là . Tính
58
45
85
40
Cho parabol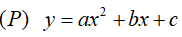 có đỉnh là tâm của một hình vuông ABCD , trong đó C,D nằm trên trục hoành và A,B nằm trên (P). Giá trị nhỏ nhất của biểu thức
có đỉnh là tâm của một hình vuông ABCD , trong đó C,D nằm trên trục hoành và A,B nằm trên (P). Giá trị nhỏ nhất của biểu thức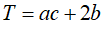 bằng bao nhiêu ?
bằng bao nhiêu ?
2
-3
4
-2
Một gia đình sản xuất cà phê nguyên chất. Do điều kiện nhà xưởng nên mỗi đợt gia đình đó sản xuất được t kg cà phê . Nếu gia đình đó bán sỉ x kg thì giá của mỗi kí được xác định bởi công thức (nghìn đồng) và chi phí để sản xuất x kg cà phê được xác định bởi công thức (nghìn đồng).
1,Tính chi phí để gia đình đó sản xuất kg cà phê thứ 10
1600 nghìn.
69 nghìn.
1100 nghìn.
1000 nghìn.
2, Để đạt được lợi nhuận tối đa, mỗi đợt gia đình đó nên sản xuất bao nhiêu kg cà phê.
Cho hàm số
Có bao nhiêu giá trị của a sao cho giá trị nhỏ nhất củatrên đoạn là bằng 5?
0
1
2
3
Cho hàm số bậc hai (P): , trong đó x là ẩn, m là tham số. Tìm tất cả các giá trị của m để (P) cắt trục hoành tại hai điểm phân biệt có hoành độ và đạt giá trị nhỏ nhất.
Gọi M và m lần lượt là GTLN và GTNN của hàm số .
Tính 4M + m.
516
534
Tìm tham số m để biểu thức có giá trị nhỏ nhất bằng 18.
Đáp án khác
Cho ( là tham số), là giá trị của hàm số tại . Biết và giá trị nhỏ nhất của hàm số là -8 Khi đó có giá trị bằng:
-5
-4
-6
3
Cho hàm số: y = + bx + c đạt giá trị nhỏ nhất bằng 2 khi x=1 và nhận giá trị bằng 3 khi x=2 . Tính abc
-6
6
-2
1
Cho hàm số có . Khi đó giá trị của b là:
Cho hàm số . Tìm m để giá trị lớn nhất của hàm số y là nhỏ nhất.
Cho hàm số . Tìm m để giá trị lớn nhất của hàm số y là nhỏ nhất.
Gọi A,B là hai giao điểm của đường thẳng và parabol . Gọi điểm thuộc trục đối xứng của sao cho nhỏ nhất. Tính .
1
2
3
4
Cho 2 số x,y thỏa mãn . Khi đó giá trị của biểu thức có giá trị bằng bao nhiêu?
0
1
2
3
Biết rằng hàm số (a,b,c là các số thực) đạt giá trị lớn nhất bằng tại và tổng lập phương các nghiệm của phương trình bằng 9 Tính
Có hai giá trị của tham số m để cho giá trị nhỏ nhất của hàm số
Trên đoạn bằng 1. Tổng của hai giá trị của m đó là :
2
Tìm các giá trị của tham số m để cho giá trị nhỏ nhất của hàm số Trên đoạn bằng 1.
m=1
Cho hàm số , . Đặt . Có bao nhiêu giá trị cuả m thỏa mãn .
0
2
3
4
Cho x,y là các số thực thỏa mãn . Giá trị lớn nhất của là
3
2
Tham số thỏa mãn giá trị lớn nhất của hàm số với đạt giá trị nhỏ nhất. Giá trị tham số a thuộc khoảng nào trong các khoảng sau?
Cho hàm số: . Biết rằng hàm số đồng biến trên . Khi đó giá trị lớn nhất của biểu thức là:
4
Đặt và , giả sử . Tính .
Cho 2 số thực thỏa mãn điều kiện .
Hỏi biểu thức có tất cả bao nhiêu ước số nguyên dương?
5
6
7
8
Cho hàm số , m là tham số. Tìm m để giá trị nhỏ nhất của đạt giá trị lớn nhất.
Cho hàm số bậc nhất ( m là tham số), có đồ thị là đường thẳng d . Khoảng cách lớn nhất từ gốc tọa độ đến d là
Biết rằng parabol cắt trục hoành tại hai điểm có hoành độ thuộc đoạn . Khi đó giá trị lớn nhất của biểu thức thuộc khoảng nào sau đây?
Cho hàm số có đồ thị đi qua điểm và cắt trục hoành tại hai điểm B, C sao cho tam giác vuông đỉnh và có diện tích . Gọi M là giá trị lớn nhất của hàm số . Tìm giá trị lớn nhất của M.
Cho hình chữ nhật ABCD , . Trên các cạnh lần lượt lấy các điểm sao cho . Độ dài của AP trong khoảng nào sau đây thì diện tích tam giác PQR đạt nhỏ nhất.
Cho hàm số ( m là tham số). Gọi S là tập hợp tất cả các giá trị của m sao cho . Khẳng định nào sau đây đúng:
Cho hàm số có đồ thị là (P) và hai điểm , . Biết điểm trên (P) thỏa mãn diện tích tam giác MAB nhỏ nhất. Tính tổng .
4
2
3
5
Tìm m để hàm số có giá trị nhỏ nhất đạt giá trị lớn nhất. Giả sử , là phân số tối giản , . Tính .
Giả sử phương trình bậc hai ẩn x (m là tham số): có hai nghiệm thỏa mãn điều kiện . Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính :
-64
-44
Cho hàm số: . Biết rằng hàm số đồng biến trên . Khi đó giá trị lớn nhất của biểu thức là:
4
Cho parabol và đường thẳng . Biết d cắt (P) tại hai điểm phân biệt A,B có hoành độ lần lượt là .Tìm giá trị nhỏ nhất của ?
Cho .Tìm giá trị lớn nhất của ?
Cho hàm số với a là tham số.Gọi M và m là giá trị lớn nhất và nhỏ nhất của hàm số trên . Biết rằng có hai giá trị của a để khi đó tổng hai giá trị của a bằng
0
1
-1
2
Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số: f(x) = 4 - 4mx + – 2m + 2 trên đoạn [0; 2] bằng 3?
0
1
2
3
Gọi a, b các số thực để biểu thức đạt giá trị lớn nhất bằng 4 và giá trị nhỏ nhất bằng -1. Tính giá trị của biểu thức .
Cho phương trình bậc hai ( x là ẩn và m là tham số). Khi đó thuộc đoạn nào để phương trình đã cho có hai nghiệm không âm và giá trị của là nhỏ nhất.
Cho hàm số Giá trị để đồ thị của hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ sao cho biểu thức đạt giá trị nhỏ nhất.
Cho phương trình: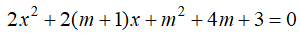 . Gọi là 2 nghiệm của phương trình. Tìm GTLN của
. Gọi là 2 nghiệm của phương trình. Tìm GTLN của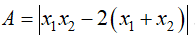
4
9
8
Cho hàm số và ba số thực thỏa mãn Gọi M là giá trị nhỏ nhất của biểu thức Giá trị M là
85
58
78
65
Cho hàm số . Tổng S tất cả các giá trị nguyên dương của m thỏa mãn điều kiện: (với S là giá trị nhỏ nhất của hàm số khi ) bằng:
Cho hàm số . Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số , với . Tổng .
Cho hàm số , thỏa mãn và biểu thức đạt giá trị lớn nhất. Tính , biết
Cho đồ thị hàm số có đỉnh . Biết giá trị nhỏ nhất của biểu thức là M khi hàm số có pt: Tính
Cho .Tìm giá trị lớn nhất của ?
Tìm m để giá trị lớn nhất của hàm số trên đoạn là giá trị nhỏ nhất.
Cho parabol ( m là tham số ) có đỉnh I. Gọi A,B là 2 điểm thuộc Ox sao cho . Khi đó có diện tích nhỏ nhất bằng :
2018
1009
4036
1008
Cho hàm số ( m là tham số). Có bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số trên bằng 7 .
1
2
0
3
Cho các số thực thỏa mãn . Gọi lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức . Khi đó giá trị của là
Giá trị m để giá trị lớn nhất của hàm số trên đạt giá trị nhỏ nhất thỏa mãn mệnh đề nào sau đây
Giá trị m để giá trị lớn nhất của hàm số trên đạt giá trị nhỏ nhất thỏa mãn mệnh đề nào sau đây
Biết rằng hàm số (a,b,c là các số thực) đạt giá trị lớn nhất bằng tại và tổng lập phương các nghiệm của phương trình bằng 9Tính
Cho đường thẳng và parabol (P): (m là tham số thực). Biết (với và phân số tối giản) là khoảng cách lớn nhất từ đỉnh I của parabol (P) đến đường thẳng . Tính .
Trong mặt phẳng tọa độ Oxy, cho hai điểm và . Điểm (với là phân số tối giản, ) nằm trên trục tung thỏa mãn tổng khoảng cách từ M tới hai điểm A và B là nhỏ nhất. Tính .
S=1
S=11
S=4
S=3
Cho hàm số . Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số , với . Tổng .
Cho Parabol . Gọi S là tổng tất cả các giá trị của m để hàm số đạt giá trị nhỏ nhất baèng -6 trên đoạn [-2; 3]. Tính tổng tất cả các phần tử của S.
8
7
2
4
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số trên đoạn bằng 3Tính tổng T các phần tử của S
Gọi lần lượt là GTLN và GTNN của hàm số . Tìm số phần tử của tập hợp ?
0
1
3
4
Cho hàm số . Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên lần lượt là ; . Tính tổng các giá trị của m tìm được, biết .
-1
-3
2
3
Xét các số thực sao cho phương trình có hai nghiệm thuộc . Giá trị lớn nhất của biểu thức là
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27(triệu đồng) và bán ra với giá là 31triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.
30 triệu đồng.
29 triệu đồng.
30,5 triệu đồng.
29,5 triệu đồng.
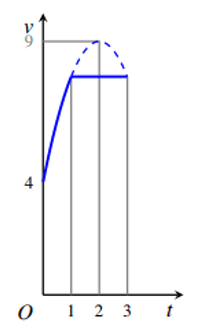
Một vật chuyển động trong 3giờ với vận tốc v(km/h) phụ thuộc vào thời gian t(h) có đồ thị của hàm số vận tốc như hình dưới. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính vận tốc v của vật tại thời điểm t=3.
Với giá trị nào của a thì bất pt sau nghiệm đúng với mọi giá trị của x :
Cho phương trình . Gọi là giá trị nhỏ nhất của tham số m để phương trình đã cho có 3nghiệm phân biệt. Khi đó:
Dây truyền đỡ nền cầu treo có dạng Parabol ACB như hình vẽ. Đầu cuối của dây được gắn chặt vào điểm A và B trên trục AA' và BB' với độ cao 30m. Chiều dài nhịp . Độ cao ngắn nhất của dây truyền trên nền cầu là OC=5m. Tính tổng chiều dài các dây cáp treo (thanh thằng đứng nối nền cầu với dây truyền)?
37
Dây truyền đỡ nền cầu treo có dạng Parabol ACB như hình vẽ. Đầu cuối của dây được gắn chặt vào điểm A và B trên trục AA' và BB' với độ cao 30m. Chiều dài nhịp A'B'=200m. Độ cao ngắn nhất của dây truyền trên nền cầu là OC=5m. Xác định tổng các chiều dài các dây cáp treo (thanh thẳng đứng nối nền cầu với dây truyền)?
34,875m
35,875m
36,875m
37,875m
Khi một quả bóng được đá lên nó sẽ đạt được độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol. Giả thiết rằng bóng được đá từ độ cao 1m. Sau đó 1 giây nó đạt độ cao 8, 5m và 2 giây sau khi đá nó đạt độ cao 6m. Hỏi sau bao lâu quả bóng chạm đất (Tính chính xác đến hàng phần trăm).
2,58s
2,59s
2,60s
2,57s
Một chiếc cổng như hình vẽ, trong đó CD=6m , AD=4m , phía trên cổng có dạng hình parabol
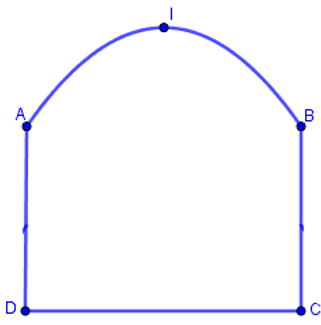
Người ta cần thiết kế cổng sao cho những chiến xe container chở hàng với bề ngang thùng xe là 4m, chiều cao là 5,2mcó thể đi qua được (chiều cao được tính từ mặt đường đến nóc thùng xe và thùng xe có dạng hình hộp chữ nhật). Hỏi đỉnh I của parabol (theo mép dưới của cổng) cách mặt đất tối thiểu là bao nhiêu ?
6,13m
6,14m
6,15m
6,16m
Cho a,b,c là các số thực thuộc đoạn [0,1]. Tìm GTLN của biểu thức
![]()
1
Cho hàm số thỏa mãn với . Biết , hỏi giá trị của nằm trong khoảng nào dưới đây ?






