26 câu hỏi
Cho hàm số \(y = {x^3} - 3{x^2} - 9x - 5\). Phương trình \(y' = 0\) có nghiệm là:
\(\left\{ { - 1;2} \right\}\).
\(\left\{ { - 1;3} \right\}\).
\(\left\{ {0;4} \right\}\).
\(\left\{ {1;2} \right\}\).
Cho hàm số \[f\left( x \right) = k\sqrt[3]{x} + \sqrt x \]\[(k \in \mathbb{R})\]. Để \[f'\left( 1 \right) = \frac{3}{2}\] thì ta chọn:
\[k = 1\].
\[k = - 3\].
\[k = 3\].
\[k = \frac{9}{2}\].
Cho hàm số \[f\left( x \right) = \frac{1}{3}{x^3} - 2\sqrt 2 {x^2} + 8x - 1\]. Tập hợp những giá trị của \[x\] để \[f'\left( x \right) = 0\] là:
\[\left\{ { - 2\sqrt 2 } \right\}\].
\[\left\{ {2;\sqrt 2 } \right\}\].
\[\left\{ { - 4\sqrt 2 } \right\}\].
\[\left\{ {2\sqrt 2 } \right\}\].
Cho hàm số \(y = 4x - \sqrt x \). Nghiệm của phương trình \(y' = 0\) là
\(x = \frac{1}{8}.\)
\(x = \sqrt {\frac{1}{8}} .\)
\(x = \frac{1}{{64}}.\)
\(x = - \frac{1}{{64}}.\)
Cho hàm số \(y = - 4{x^3} + 4x\). Để \(y' \ge 0\) thì \[x\]nhận các giá trị thuộc tập nào sau đây ?
\(\left[ { - \sqrt 3 ;\sqrt 3 } \right].\)
\(\left[ { - \frac{1}{{\sqrt 3 }};\frac{1}{{\sqrt 3 }}} \right].\)
\(\left( { - \infty ; - \sqrt 3 } \right] \cup \left[ {\sqrt 3 ; + \infty } \right).\)
\(\left( { - \infty ; - \frac{1}{{\sqrt 3 }}} \right] \cup \left[ {\frac{1}{{\sqrt 3 }}; + \infty } \right).\)
\(f'(x) \ge 0\) với \(f(x) = 2{x^3} - 3{x^2} + 1\)
\(\left[ \begin{array}{l}x \le 0\\x \ge 1\end{array} \right.\)
\(x \le 1\)
\(x \ge 0\)
\(0 \le x \le 1\)
\(f'(x) < 0\) với \(f(x) = - 2{x^4} + 4{x^2} + 1\)
\(\left[ \begin{array}{l} - 1 < x < 0\\x > 1\end{array} \right.\)
\( - 1 < x < 0\)
\(x > 1\)
\(x < 0\)
Cho hàm số \(y = - 3{x^3} + 25.\) Các nghiệm của phương trình \[y' = 0\] là.
\(x = \pm \frac{5}{3}\).
\(x = \pm \frac{3}{5}\).
\(x = 0\).
\(x = \pm 5\).
Cho hàm số 
. Các nghiệm của phương trình 
là
Cho hàm số 
. Tập nghiệm của phương trình 
là
Cho hàm số 
. Tập nghiệm của phương trình 
là
Tìm số \[f\left( x \right) = {x^3} - 3{x^2} + 1.\] Đạo hàm của hàm số \[f\left( x \right)\] âm khi và chỉ khi.
\[0 < x < 2\].
\[x < 1\].
\[x < 0\]hoặc \[x > 1.\]
\[x < 0\]hoặc \[x > 2.\]
Cho hàm số 
. Để 
thì x nhận các giá trị thuộc tập nào sau đây?
Cho hàm số 
. Để 
thì x nhận các giá trị thuộc tập nào sau đây?
Cho hàm số 
. Để 
thì x nhận các giá trị thuộc tập nào sau đây?
Cho hàm số \(y = \frac{3}{{1 - x}}\). Để \(y' < 0\) thì x nhận các giá trị thuộc tập nào sau đây?
1.
3.
.
\(\mathbb{R}\).
Cho hàm số \(f(x) = \frac{{1 - 3x + {x^2}}}{{x - 1}}\). Tập nghiệm của bất phương trình \(f'(x) > 0\) là
\(\mathbb{R}\backslash \left\{ 1 \right\}.\)
\(\emptyset .\)
\(\left( {1; + \infty } \right)\).
\(\mathbb{R}.\)
Cho hàm số \(y = 3{x^3} + {x^2} + 1\). Để \(y' \le 0\) thì \(x\) nhận các giá trị thuộc tập nào sau đây
\(\left[ { - \frac{2}{9};0} \right].\)
\(\left[ { - \frac{9}{2};0} \right].\)
\(\left( { - \infty ; - \frac{9}{2}} \right] \cup \left[ {0; + \infty } \right).\)
\(\left( { - \infty ; - \frac{2}{9}} \right] \cup \left[ {0; + \infty } \right).\)
Cho hàm số 
. Tập nghiệm của bất phương trình
là
\{0}.
với \(f(x) = x + \sqrt {{x^2} + 1} \)
\(x \ge \frac{1}{{\sqrt 3 }}\)
\(x > \frac{1}{{\sqrt 3 }}\)
\(x < \frac{1}{{\sqrt 3 }}\)
\(x \ge \frac{2}{{\sqrt 3 }}\)
\(f'(x) > 0\) với \(f(x) = x + \sqrt {4 - {x^2}} \).
\( - 2 \le x \le \sqrt 2 \)
\(x \le \sqrt 2 \)
\( - 2 \le x\)
\(x < 0\)
Cho hàm số 
. Tập nghiệm của bất phương trình 
là
Cho hàm số 
. Tập nghiệm của bất phương trình 
là
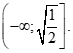
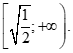
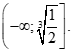
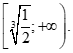
Cho hàm số \[f(x) = 2mx - m{x^3}\]. Số \[x = 1\] là nghiệm của bất phương trình \[f'(x) \le 1\] khi và chỉ khi:
\[m \ge 1.\]
\[m \le - 1.\]
\[ - 1 \le m \le 1.\]
\[m \ge - 1.\]
Tìm \(m\) để các hàm số \(y = (m - 1){x^3} - 3(m + 2){x^2} - 6(m + 2)x + 1\) có \(y' \ge 0,{\rm{ }}\forall x \in \mathbb{R}\)
\(m \ge 3\)
\(m \ge 1\)
\(m \ge 4\)
\(m \ge 4\sqrt 2 \)
Tìm \(m\) để các hàm số \(y = \frac{{m{x^3}}}{3} - m{x^2} + (3m - 1)x + 1\) có \(y' \le 0,{\rm{ }}\forall x \in \mathbb{R}\).
\(m \le \sqrt 2 \)
\(m \le 2\)
\(m \le 0\)
\(m < 0\)
