150 câu trắc nghiệm Nguyên hàm - Tích phân nâng cao (P5)

Cho parabol (P): y= $x^2+m$ . Gọi  (d) là tiếp tuyến với  (P) qua O có hệ số góc k > 0. Xác định m để thể tích vật thể được sinh ra khi hình phẳng giới hạn bởi (P), (d)  và trục Oy quay quanh trục Oy bằng 6$\mathrm{\pi }$.

Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1, y = x và đồ thị hàm số $y = \frac{x^2}{4}$   trong miền $x\ge 0, y\le 1$ là phân số tối giản $\frac{a}{b}$ . Khi đó b - a bằng

Diện tích hình phẳng giới hạn bởi các đường thẳng $y = \left\{\begin{array}{l}-x, nếu x\le 1\\ x-2, nếu x>1\end{array}\right.$ và y = $\frac{10}{3}x - x^2$  là $\frac{a}{b}$ (với $\frac{a}{b}$ là phân số tối giản) . Khi đó a + 2b bằng

Cho hàm số f(x) liên tục trên R và f(2) = 16,  ${\int }_0^{2}f\left(x\right)dx = 4$. Tính  I = ${\int }_0^{1}xf\text{'}\left(2x\right)dx$

Cho hàm số f(x) liên tục trên R và các tích phân  ${\int }_0^{\frac{\mathrm{\pi }}{4}}f(\tan x)dx$ = 4 và ${\int }_0^1\frac{x^{2}f\left(x\right)}{x^2+1}dx=2$, tính tích phân I = ${\int }_0^{1}f\left(x\right)dx$

Tính diện tích hình phẳng giới hạn bởi các đường sau: y = xsin2x, y = 2x,  $x = \frac{\mathrm{\pi }}{2}$

Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị $y = x^2- 4x + 6$ và y = $-x^2-2x + 6$

Biết là ${\int }_{\frac{2\mathrm{\pi }}{3}}^{\mathrm{\pi }}\frac{1 - x\tan x}{x^2\cos x + x}dx = \ln \left|\frac{\mathrm{\pi }-\mathrm{a}}{\mathrm{\pi }-\mathrm{b}}\right|$ ( a,b $\in \mathrm{\mathbb{Z}}$). Tính P = a + b.

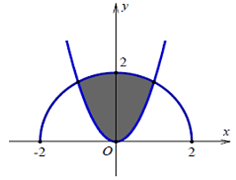
Cho (H) là hình phẳng giới hạn bởi parabol y = $\sqrt{3}{x}^2$ và nửa đường tròn có phương trình y = $\sqrt{4 -x^2}$ với $-2 \le x\le 2$ (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [1; 4], f(1) = 12 và ${\int }_1^{4}f\text{'}\left(x\right)dx = 17$ .Giá trị của f(4) bằng

Cho ${\int }_0^1\frac{1}{\sqrt{x+2} + \sqrt{x+1}}dx = a\sqrt{b} - \frac{8}{3}\sqrt{a}+\frac{2}{3} (a,b\in {\mathrm{\mathbb{N}}}^{*})$ .Tính a + 2b

Một đám vi khuẩn tại ngày thứ x có số lượng là N(x). Biết rằng N'(x) =$\frac{2000}{1+x}$ và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con?

Cho  ${\int }_1^{2}f(x^2+1)xdx = 2$. Khi đó I = ${\int }_2^{5}f\left(x\right)dx$ bằng

Biết ${\int }_a^b(2x-1)dx = 1$. Khẳng định nào sau đây đúng?

Xét hàm số f(x) liên tục trên đoạn [0; 1] và thỏa mãn  2f(x) + 3f(1-x) = $\sqrt{1-x^2}$ .Tính I = ${\int }_0^{1}f\left(x\right)dx$

Cho hàm số y = f(x) có $1\le f\text{'}\left(x\right)\le 4$   với mọi $x\in \left[2;5\right]$. Hỏi khẳng định nào dưới đây là khẳng định đúng?

Cho m thỏa mãn ${\int }_1^2\left[m^2+\left(4-4m\right)x +4x^3\right]dx = {\int }_2^{4}2xdx$. Nghiệm của phương trình ${\log }_3 \left(x+m\right) = 1$ là:

Tính tích phân $I = {\int }_1^5\frac{1}{x\sqrt{3x + 1}}dx$   được kết quả I = aln3 + bln5 với a, b là các số hữu tỉ. Giá trị của a² + ab + 3b²  là

Cho ${\int }_1^{2}f\left(x\right)dx = -3$   . Tính  ${\int }_2^{4}f\left(\frac{x}{2}\right)dx$

Cho hàm số f(x) thỏa mãn ${\int }_0^1(x+1)f\text{'}\left(x\right)dx = 10$ và 2f(1) – f(0) = 2. Tính  I = ${\int }_0^{1}f\left(x\right)dx$

Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ${\int }_0^{2}F\left(x\right)g\left(x\right)dx$ = 3  . Tính tích phân hàm:  ${\int }_0^{2}G\left(x\right)f\left(x\right)dx$

Tính S  hình phẳng được giới hạn bởi các đường $y = \frac{3^x-1}{(3^{-x}+1)\sqrt{3^x+1}}$ ; y = 0; x=1

Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x² , y = 4x - 4 và y = -4x - 4

Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.

Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (e^x + 1)x

Tính diện tích giới hạn bởi các đường cong y = (x - 1)ln(x + 1) và trục hoành

Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = $\frac{1}{1+\sqrt{4-3x}}$

Và y = 0; x = 0; x = 1 xung quanh Ox

Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = $\sqrt{x\left(3^x+1\right)}$  trục hoành và x = 1 xung quanh trục hoành.

Gọi D là miền giới hạn bởi (P): y = 2x - x² và trục hoành. Tính thể tích vật thể V do ta quay (D) xung quanh trục  Oy.

Tổn thương ở vị trí nào không gây ù tai: