30 câu hỏi
Tìm nguyên hàm:
tanx - 2x + sin2x + C
tanx - 1,5x + 0,25 sin2x + C
cot2x - 0,5 x - cos2x + C
Đáp án khác
Tìm nguyên hàm:
3x + sin4x + sin8x + C
2x - cos2x - sin4x + C
+ sin4x + sin8x + C
Đáp án khác
Tìm nguyên hàm:
Tìm nguyên hàm:
x.lnx + C
Đáp án khác
Tìm nguyên hàm
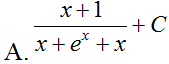
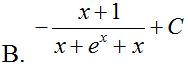
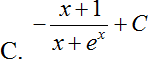
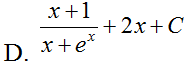
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
Kết quả tính bằng:
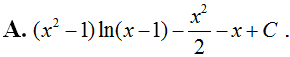
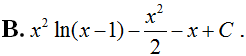
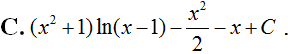
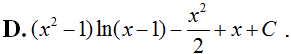
Tính bằng:
Tính bằng:
Biết hàm số là một nguyên hàm của hàm số . Khi đó tổng của a và b là
3.
2.
0.
1.
Tìm nguyên hàm của hàm số
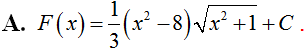
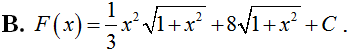
![]()
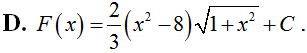
Tìm nguyên hàm của hàm số:
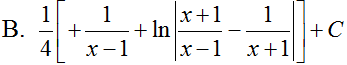
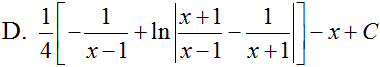
Tìm nguyên hàm của hàm số:
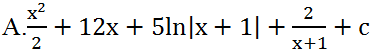
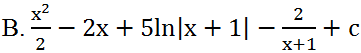
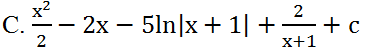
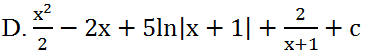
Tính nguyên hàm của hàm số sau:
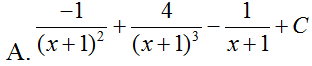
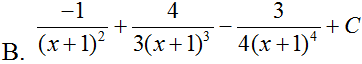
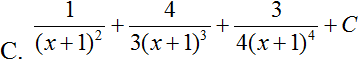
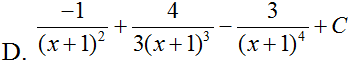
Tính . Hãy chọn đáp án đúng.
![]()
![]()
![]()
![]()
Biết hàm số là một nguyên hàm của hàm số . Khi đó tích của m và n là
2
-2
Biết hàm số F(x) là một nguyên hàm của hàm số có đồ thị đi qua điểm (e; 2016) . Khi đó hàm số F(1) là
Một nguyên hàm F(x) của hàm số thỏa mãn F(0) = 1. Chọn kết quả đúng
![]()
![]()
![]()
![]()
Một nguyên hàm F(x) của hàm số thỏa mãn . Khi đó F(x) là hàm số nào dưới đây?
F(x) = xtanx + ln|cosx| + 2017.
F(x) = xtanx – ln|cosx| + 2018.
F(x) = xtanx + ln|cosx| + 2016.
F(x) = xtanx – ln|cosx| + 2017.
Tính . Chọn kết quả đúng
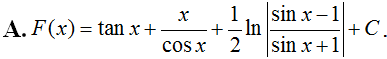
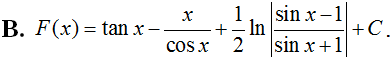
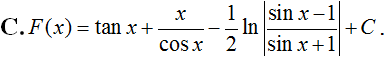
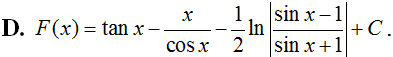
Một nguyên hàm F(x) của hàm số thỏa mãn điều kiện là
![]()
![]()
![]()
![]()
Một nguyên hàm F(x) của hàm số thỏa mãn đồ thị của hai hàm số F(x) và f(x) cắt nhau tại một điểm nằm trên trục tung là:
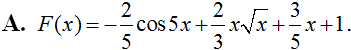
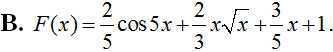
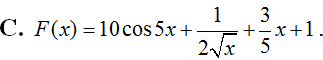
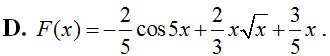
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 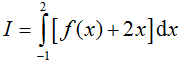 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
I = 6.
I = 10.
I = 3.
I = 9.
Cho Tính
I = 14.
I =-14.
I =7.
I =-7.
Cho hàm số f(x) liên tục trên đoạn [0; 10] thỏa mãn . Tính .
P = 10.
P = 4.
P = 7.
P = -4.
Hàm số là một nguyên hàm cùa hàm số thì a + b + c bằng:
3.
1.
3.
-2.
Một nguyên hàm F(x) của hàm số f(x) = a + bcos2x thỏa mãn là
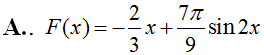


Cho hàm số là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
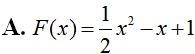
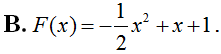
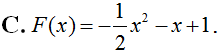
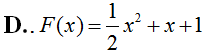
Một nguyên hàm F(x) của hàm số f(x) = tanx.sin2x thỏa mãn điều kiện là
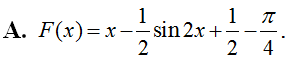
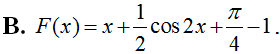
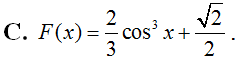
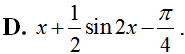
Cho hàm số f(x)= có nguyên hàm là F(x). Đồ thị hàm số y = F(x) cắt trục tung tại điểm A(0; 2). Khi đó F(x) là
F(x) = tanx – x + 2.
F(x) = tanx + 2.
F(x) = cotx – x + 2.








