15 câu hỏi
I. Nhận biết
Chu vi đường tròn có bán kính \[R = 9\] là
\[9\pi .\]
\[18\pi .\]
\[27\pi .\]
\[12\pi .\]
Công thức tính diện tích hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính \[R\] và \[r\] (với \[R > r)\] là
\[{S_v} = \pi {R^2} - {r^2}.\]
\[{S_v} = \pi {\left( {R - r} \right)^2}.\]
\[{S_v} = \pi \left( {{R^2} - {r^2}} \right).\]
\[{S_v} = \pi \left( {{r^2} - {R^2}} \right).\]
Tỉ số giữa độ dài cung \[n^\circ \] và chu vi đường tròn (cùng bán kính) luôn bằng
\[\frac{1}{n}.\]
\[\frac{1}{2}.\]
\[\frac{n}{{180}}.\]
\[\frac{n}{{360}}.\]
Phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung tròn đó được gọi là
Hình quạt tròn.
Hình vành khuyên.
Hình vành khăn.
Hình viên phân.
Độ dài cung \[30^\circ \] của một đường tròn có bán kính \[4{\rm{\;dm}}\] là
\[\frac{{4\pi }}{3}{\rm{\;dm}}.\]
\[\frac{{2\pi }}{3}{\rm{\;dm}}.\]
\[\frac{\pi }{3}{\rm{\;dm}}.\]
\[\frac{\pi }{6}{\rm{\;dm}}.\]
II. Thông hiểu
Số đo \[n^\circ \] của cung tròn có độ dài \[30,8{\rm{\;cm}}\] trên đường tròn có bán kính \[22{\rm{\;cm}}\] (lấy \[\pi \approx 3,14\] và làm tròn đến độ) là
\[85^\circ .\]
\[65^\circ .\]
\[70^\circ .\]
\[80^\circ .\]
Cho tam giác \[ABC\] vuông tại \[A,\] cạnh \[AB = 5{\rm{\;cm}},\,\,\widehat {B\,} = 60^\circ .\] Đường tròn tâm \[I,\] đường kính \[AB\] cắt \[BC\] ở \[D.\] Khẳng định nào sau đây là sai?
Độ dài cung nhỏ \[BD\] của đường tròn \[\left( I \right)\] là \[\frac{\pi }{6}{\rm{\;cm}}.\]
\[AD \bot BC.\]
\[D\] thuộc đường tròn đường kính \[AC.\]
Số đo của cung nhỏ \[BD\] là \(60^\circ .\)
Cho đường tròn \[\left( {O;10{\rm{\;cm}}} \right)\] đường kính \[AB.\] Điểm \[M \in \left( O \right)\] sao cho \[\widehat {BAM} = 45^\circ .\] Diện tích hình quạt \[AOM\] bằng
\[25\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[\frac{{25}}{2}\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[5\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[50\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Cho đường tròn \[\left( O \right)\] đường kính \[AB = 2\sqrt 2 {\rm{\;cm}}.\] Điểm \[C \in \left( O \right)\] sao cho \[\widehat {ABC} = 30^\circ .\] Diện tích hình quạt \[BAC\] bằng
\[\frac{{4\sqrt 2 }}{3}\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[\frac{{2\sqrt 2 }}{3}\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[\frac{{4\pi }}{3}{\rm{\;c}}{{\rm{m}}^2}.\]
\[\frac{{8\pi }}{3}{\rm{\;c}}{{\rm{m}}^2}.\]
Cho tam giác \[ABC\] đều có ba đỉnh nằm trên đường tròn \[\left( O \right).\] Độ dài các cung \[AB,BC,CA\] đều bằng \[6\pi {\rm{\;cm}}.\] Diện tích của đường tròn \[\left( O \right)\] là
\[32\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[18\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[9\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[27\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có đường kính lần lượt là \[8{\rm{\;cm}}\] và \[6{\rm{\;cm}}\] bằng
\[\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[7\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[25\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[\frac{7}{2}\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Cho hình vành khuyên giới hạn bởi hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O;r} \right),\] biết rằng \[r = 7{\rm{\;cm}}\] và \[R\] gấp \[3\] lần \[r\]. Diện tích của hình vành khuyên đó bằng
\[392\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[392{\rm{\;c}}{{\rm{m}}^2}.\]
\[490\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[245\pi {\rm{\;c}}{{\rm{m}}^2}.\]
III. Vận dụng
Cho sân cỏ như hình vẽ, biết rằng \[OB = 10{\rm{\;m}},\,\,\widehat {AOB} = 80^\circ .\]
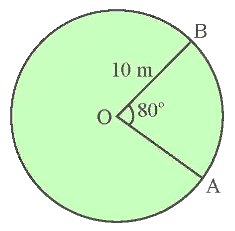
Độ dài đoạn hàng rào quanh sân từ \[A\] đến \[B\] của sân cỏ (làm tròn kết quả đến hàng phần trăm) là
\[488,69{\rm{\;m}}{\rm{.}}\]
\[69,81{\rm{\;m}}.\]
\[13,96{\rm{\;m}}.\]
\[6,98{\rm{\;m}}.\]
Cho hình “viên phân” (phần màu xanh) được giới hạn bởi dây cung có độ dài \[55{\rm{\;cm}}\] và cung có số đo \[95^\circ \] (hình vẽ).
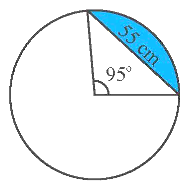
Diện tích hình viên phân đó (làm tròn kết quả đến hàng phần trăm) là
\[680,65{\rm{\;c}}{{\rm{m}}^2}.\]
\[460,41{\rm{\;c}}{{\rm{m}}^2}.\]
\[692,98{\rm{\;c}}{{\rm{m}}^2}.\]
\[1153,39{\rm{\;c}}{{\rm{m}}^2}.\]
Hình vẽ dưới đây mô tả mặt cắt của một chiếc đèn led có dạng hai hình vành khuyên màu trắng với bán kính các đường tròn lần lượt là \[15{\rm{\;cm}},\,\,18{\rm{\;cm}},\,\,21{\rm{\;cm}},\,\,24{\rm{\;cm}}.\]

Khi đó tổng diện tích hai hình vành khuyên đó bằng
\[234\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[99\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[135\pi {\rm{\;c}}{{\rm{m}}^2}.\]
\[216\pi {\rm{\;c}}{{\rm{m}}^2}.\]
