10 câu hỏi
Cho tứ giác ABCD nội tiếp đường tròn biết A = 2C. Vậy số đo C bằng
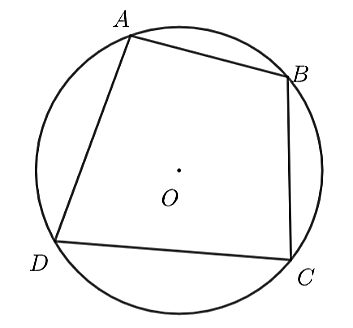
60°.
120°.
50°.
100°.
Cho tứ giác MNPQ nội tiếp đường tròn với \[\widehat {MQP} - \widehat {MNP} = 10^\circ \]. Số đo góc MQP bằng
90°.
95°.
80°.
100°.
Cho tứ giác ABCD nội tiếp đường tròn, biết \[\widehat A = 100^\circ \], \[\widehat B = 70^\circ \]. Vậy số đo góc C; D lần lượt bằng
\[\widehat C = 80^\circ ;\widehat D = 100^\circ \].
\[\widehat C = 80^\circ ;\widehat D = 70^\circ \].
\[\widehat C = 80^\circ ;\widehat D = 140^\circ \].
\[\widehat C = 80^\circ ;\widehat D = 110^\circ \].
Cho hình vẽ bên. Khi đó, góc BCD bằng
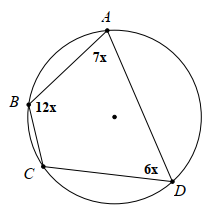
120°.
60°.
70°.
110°.
Cho tứ giác MNPQ nội tiếp đường tròn (O) và \[\widehat {NPQ} = 100^\circ \], số đo góc NMQ bằng
80°.
160°.
240°.
140°.
Cho tam giác ABC vuông tại A và lấy điểm E bất kì trên cạnh AB. Qua B vẽ một đường thẳng vuông góc với CE tại D và cắt tia CA tại H, biết \[\widehat {ACB} = 34^\circ \], số đo góc \[ADH\] bằng
38°.
40°.
34°.
36°.
Cho tam giác ABC có CK và BD là hai đường cao, biết \[\widehat {ACB} = 50^\circ \]. Số đo góc AKD bằng
50°.
40°.
60°.
70°.
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường thẳng AB, CD cắt nhau tại M và hai đường thẳng AD, BC cắt nhau tại N như hình vẽ. Biết các góc ANB = a°; AMD = b°.
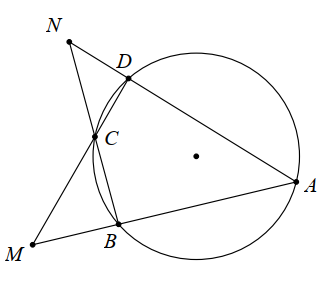
Số đo góc BAD bằng
\[90^\circ - \frac{{a^\circ + b^\circ }}{2}.\]
\[180^\circ - \frac{{a^\circ + b^\circ }}{2}.\]
\[90^\circ + \frac{{a^\circ + b^\circ }}{2}.\]
\[90^\circ - a^\circ - b^\circ .\]
Cho tứ diện ABCD nội tiếp đường tròn (O), hai đường thẳng AB, CD cắt nhau tại M và hai đường thẳng AD, BC cắt nhau tại N như hình vẽ. Biết các góc ANB = a°; góc AMD = b°.

Số đo góc BCD bằng
\[90^\circ + \frac{{a^\circ + b^\circ }}{2}.\]
\[180^\circ - \frac{{a^\circ + b^\circ }}{2}.\]
\[90^\circ + a^\circ + b^\circ .\]
\[180^\circ - a^\circ + b^\circ .\]
Cho tứ giác ABCD nội tiếp đường tròn (O; R) có AB = BC = R. Số đo góc ADC là
120°.
140°.
70°.
60°.
