9 câu hỏi
Cho hình cầu có đường kính d = 6 cm. Diện tích mặt cầu là
36π (cm2).
9π (cm2).
12π (cm2).
36 (cm2).
Cho mặt cầu có thể tích V = 288π (cm3). Tính đường kính mặt cầu.
6 cm.
12 cm.
8 cm.
16 cm.
Thể tích của quả bóng nhựa hình cầu với đường kính 10 cm là
\[\frac{{4000}}{3}\] cm3.
\[\frac{{500}}{3}\] cm3.
\[\frac{{4000\pi }}{3}\] cm3.
\[\frac{{500\pi }}{3}\] cm3.
Một quả bóng rổ (khi bơm căng) có đường kính 24 cm. Tìm thể tích của quả bóng rổ đó (kết quả làm tròn đến hàng đơn vị).
B. 7239 cm3.
7238 cm3.
7237 cm3.
7328 cm3.
Cho tam giác ABC đều có cạnh AB = 8 cm, đường cao AH. Khi đó thể tích hình cầu tạo thành khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH.
\[\frac{{\pi {a^3}}}{{54}}.\]
\[\frac{{\pi \sqrt 3 {a^3}}}{{72}}.\]
\[\frac{{\pi \sqrt 3 {a^3}}}{{54}}.\]
\[\frac{{\pi {a^3}}}{{72}}.\]
Cho một tam giác ABC đều có cạnh AB = 12 cm, đường cao AH. Khi đó thể tích hình cầu được tạo thành khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH.
\[32\sqrt 3 .\]
\[16\pi \sqrt 3 .\]
\[8\pi \sqrt 3 .\]
\[32\pi \sqrt 3 .\]
Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng 6 cm. Tính diện tích mặt cầu được tạo thành khi quay quanh nửa đường tròn ngoại tiếp tam giác ABC một vòng quanh cạnh BC.
72 (cm2).
18π (cm2).
36π (cm2).
72π (cm2).
Cho hình chữ nhật ABCD có AB = 8 cm, AD = 6 cm. Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật ABCD quay quanh đường thẳng MN với M là trung điểm AD, N là trung điểm BC
50π (cm2).
100π (cm2).
100 (cm2).
25π (cm2).
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Nếu diện tích toàn phần của hình lập phương là 24 cm2 thì diện tích mặt cầu là
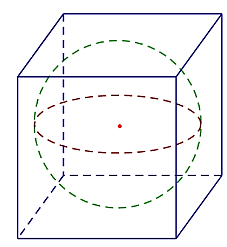
4π.
4.
2π.
2.
