10 bài tập Một số bài toán thực tế liên quan đến Đường tiệm cận của đồ thị hàm số (có lời giải)

Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \[C(x) = \frac{{50x + 2000}}{x}\]. Tìm các đường tiệm cận của hàm số C(x).

Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức y(t) = \[y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\], với y được tính theo mg/l và t được tính theo giờ, t ≥ 0. Tìm các đường tiệm cận của đồ thị hàm số y(t). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn?

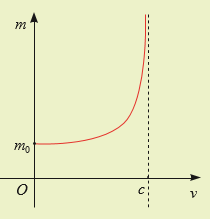
Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \[m(v) = \frac{{{m_o}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\], trong đó mo là khối lượng nghỉ của hạt, c = 300000 km/s là tốc độ ánh sáng. Tìm tiệm cận của đồ thị hàm số khối lượng hạt \[m(v) = \frac{{{m_o}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\] . Từ đó, có nhận xét gì khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt thay đổi như thế nào?

Một bể chứa 5 000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút.

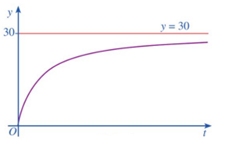
a) Chứng tỏ nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là \[f(t) = \frac{{30t}}{{200 + t}}\].

b) Xem y = f(t) là một hàm số xác định trên nửa khoảng [0 ; + \[\infty \]), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

c) Nêu nhận xét về nồng độ muối trong bể sau thời gian t ngày càng lớn.

Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức: \[S(x) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\], trong đó x≥ 1.

a) Xem y = S(x) là một hàm số xác định trên nửa khoảng [1 ;+ \[\infty \]), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.

Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau 1 ngày phân rã được cho bởi hàm số \[m(t) = 15{e^{ - 0,0012t}}\]. Khối lượng m(t) thay đổi ra sao khi \[t \to  + \infty \]? Điều này thể hiện trên Hình vẽ bên như thế nào?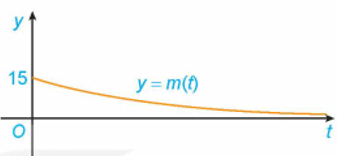

Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là \[C(p) = \frac{{45p}}{{100 - p}}\] (triệu đồng), với \[0 \le p < 100\]. Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa thực tiễn của đường tiệm cận này.

Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x)=2x+50 (triệu đồng). Khi đó \[f(x) = \frac{{C(x)}}{x}\] là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và \[\mathop {\lim }\limits_{x \to  + \infty } f(x) = 2\]. Tính chất này nói lên điều gì?

Một mảnh vườn hình chữ nhật có diện tích bằng 144 m2. Biết độ dài một cạnh của mảnh vườn là x (m).

a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.

b) Tìm các tiệm cận của đồ thị hàm số P(x).