18 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ lựa chọn một phương án.
Một con lắc đơn chiều dài \[\ell \], dao động điều hòa với biên độ góc \[{\alpha _0}\].Tích số \[\ell {\alpha _0}\] được gọi là
năng lượng của dao động.
biên độ cong của dao động.
chu kì của dao động.
tần số của dao động.
Cho dao động điều hòa với phương trình vận tốc \[v = {v_0}\cos \left( {\omega t} \right)\]. Biên độ của dao động này là
\[{v_0}\].
\[{v_0}\omega \].
\[\frac{{{v_0}}}{\omega }\].
\[\frac{\omega }{{{v_0}}}\].
Một vật dao động tắt dần có các đại lượng nào sau đây giảm liên tục theo thời gian?
Li độ và gia tốc.
Li độ và cơ năng.
Biên độ và cơ năng.
Vận tốc và gia tốc.
Một con lắc lò xo có tần số dao động riêng f0. Khi tác dụng vào nó một ngoại lực cưỡng bức tuần hoàn có tần số f thì xảy ra hiện tượng cộng hưởng. Hệ thức nào sau đây đúng?
f = 4f0.
f = 3f0.
f = 2f0.
f = f0.
Nếu tăng chiều dài của con lắc đơn lên 4 lần thì chu kì dao động của con lắc sẽ
không thay đổi.
tăng lên 4 lần.
tăng lên 2 lần.
giảm đi 2 lần.
Một con lắc đơn gồm vật nặng, dây treo có chiều dài \[l\] được kích thích dao động điều hòa tại nơi có gia tốc trọng trường \[g\]. Chu kì dao động của con lắc được xác định bởi
\[\sqrt {\frac{l}{g}} \].
\[2\pi \sqrt {\frac{l}{g}} \].
\[\sqrt {\frac{g}{l}} \].
\[2\pi \sqrt {\frac{g}{l}} \].
Một dao động điều hòa có phương trình \[x = 10\cos \left( {10\pi t} \right)\]cm, \[t\] được tính bằng giây. Tốc độ cực đại của chất điểm này trong quá trình dao động là
100 cm/s.
10 cm/s.
\[10\pi \]cm/s.
\[100\pi \]cm/s.
Vật nặng của một con lắc lò xo di chuyển lên xuống sau khi được kích thích dao động tại thời điểm \[t = 0\]. Đồ thị biểu diễn li độ của vật nặng theo thời gian được cho như hình vẽ.
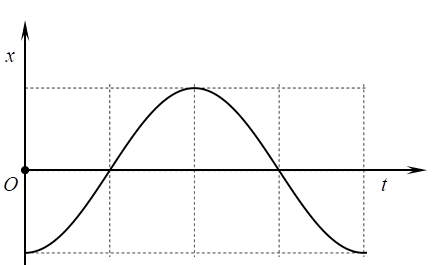
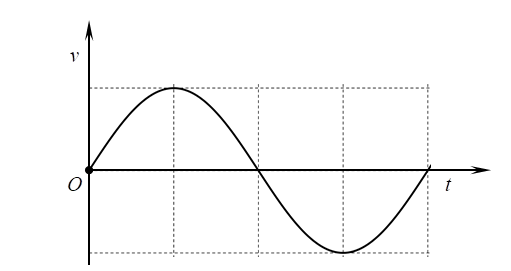
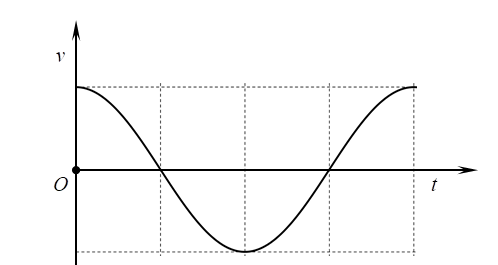
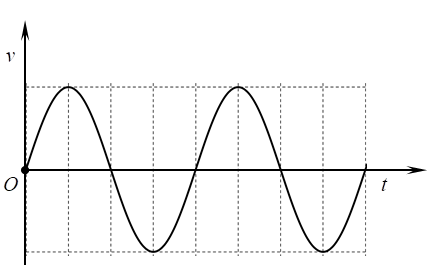
Đồ thị nào sau đây biểu diễn đúng vận tốc của vật theo thời gian?
|
|
|
Hình A |
Hình B |
|
|
|
Hình C |
Hình D |
Hình A.
Hình B.
Hình C.
Hình D.
Một chất điểm dao động điều hoà theo phương trình \[x = 2\cos \left( {2\pi t} \right)\](\[x\] tính bằng cm; \[t\] tính bằng s). Tại thời điểm \[t = \frac{1}{3}\]s chất điểm có vận tốc bằng
\[ - 2\pi \]cm/s.
\[2\pi \]cm/s.
\[2\pi \sqrt 3 \]cm/s.
–\[2\pi \sqrt 3 \] cm/s.
Một con lắc lò xo gồm một vật nhỏ có khối lượng \[m\] và lò xo nhẹ, dao động điều hòa dọc theo trục \[Ox\] quanh vị trí cân bằng O với tần số góc là \[\omega \]. Biểu thức lực kéo về tác dụng lên vật theo li độ \[x\] là
\[F = m\omega x\].
\[F = - m{\omega ^2}x\].
\[F = m{\omega ^2}x\].
\[F = - m\omega x\].
Một con lắc đơn có chiều dài \[\ell = 1,2\]m dao động nhỏ với tần số góc bằng 2,86 rad/s tại nơi có gia tốc trọng trường \[g\]. Giá trị của \[g\] tại đó bằng
9,82 m/s2.
9,88 m/s2.
9,85 m/s2.
9,80 m/s2.
Một chất điểm dao động điều hòa trên trục Ox, động năng Wđ của chất điểm này biến thiên với chu kì 1 s. Chu kì dao động của chất điểm này là
1 s.
2 s.
3 s.
4 s.
Một chất điểm dao động tuần hoàn với chu kì bằng 1 s. Biết quỹ đạo chuyển động của chất điểm dài 8 cm. Tính quãng đường chất điểm đi được trong 6 s.
72 cm.
48 cm.
96 cm.
108 cm
Một vật dao động điều hòa với biên độ bằng 4 cm. Khi pha của dao động bằng \[\frac{\pi }{3}\] thì li độ của vật bằng:
2 cm.
4 cm.
- 2 cm.
- 4 cm.
Dao động điều hòa đổi chiều khi
lực tác dụng có độ lớn cực đại.
lực tác dụng có độ lớn cực tiểu.
lực tác dụng biến mất.
không có lực nào tác dụng vào vật.
Gia tốc của một chất điểm dao động điều hòa biến thiên
cùng tần số và cùng pha với li độ.
cùng tần số và ngược pha với li độ.
khác tần số và vuông pha với li độ.
khác tần số và cùng pha với li độ.
Một vật dao động điều hòa có biên độ \[A\] và chu kì \[T\], mốc thời gian (\[t = 0\]) là lúc vật đi qua vị trí cân bằng, phát biểu nào sau đây là sai?
Sau \[\frac{T}{2}\], vật đi được quãng đường \[2A\].
Sau \[\frac{T}{8}\], vật đi được quãng đường \[\frac{A}{2}\].
Sau \[\frac{T}{4}\], vật đi được quãng đường\[A\].
Sau \[\frac{T}{{12}}\], vật đi được quãng đường \[\frac{A}{2}\].
Một con lắc đơn dao động điều hòa với biên độ góc \({\alpha _0}\). Lấy mốc thế năng ở vị trí cân bằng. Ở vị trí con lắc có động năng bằng thế năng thì li độ góc của nó bằng:
\( \pm \frac{{{\alpha _0}}}{{2\sqrt 2 }}\).
\( \pm \frac{{{\alpha _0}}}{{2\sqrt 3 }}\).
\( \pm \frac{{{\alpha _0}}}{{\sqrt 2 }}\).
\( \pm \frac{{{\alpha _0}}}{2}\).
