Trắc nghiệm ôn tập Cuối kì 1 Vật Lí 11 Kết nối tri thức (có đúng sai, trả lời ngắn) có đáp án - Bài tự luyện số 1
28 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ lựa chọn một phương án.
Một con lắc đơn chiều dài \[\ell \], dao động điều hòa với biên độ góc \[{\alpha _0}\].Tích số \[\ell {\alpha _0}\] được gọi là
năng lượng của dao động.
biên độ cong của dao động.
chu kì của dao động.
tần số của dao động.
Cho dao động điều hòa với phương trình vận tốc \[v = {v_0}\cos \left( {\omega t} \right)\]. Biên độ của dao động này là
\[{v_0}\].
\[{v_0}\omega \].
\[\frac{{{v_0}}}{\omega }\].
\[\frac{\omega }{{{v_0}}}\].
Một vật dao động tắt dần có các đại lượng nào sau đây giảm liên tục theo thời gian?
Li độ và gia tốc.
Li độ và cơ năng.
Biên độ và cơ năng.
Vận tốc và gia tốc.
Một con lắc lò xo có tần số dao động riêng f0. Khi tác dụng vào nó một ngoại lực cưỡng bức tuần hoàn có tần số f thì xảy ra hiện tượng cộng hưởng. Hệ thức nào sau đây đúng?
f = 4f0.
f = 3f0.
f = 2f0.
f = f0.
Nếu tăng chiều dài của con lắc đơn lên 4 lần thì chu kì dao động của con lắc sẽ
không thay đổi.
tăng lên 4 lần.
tăng lên 2 lần.
giảm đi 2 lần.
Một con lắc đơn gồm vật nặng, dây treo có chiều dài \[l\] được kích thích dao động điều hòa tại nơi có gia tốc trọng trường \[g\]. Chu kì dao động của con lắc được xác định bởi
\[\sqrt {\frac{l}{g}} \].
\[2\pi \sqrt {\frac{l}{g}} \].
\[\sqrt {\frac{g}{l}} \].
\[2\pi \sqrt {\frac{g}{l}} \].
Một dao động điều hòa có phương trình \[x = 10\cos \left( {10\pi t} \right)\]cm, \[t\] được tính bằng giây. Tốc độ cực đại của chất điểm này trong quá trình dao động là
100 cm/s.
10 cm/s.
\[10\pi \]cm/s.
\[100\pi \]cm/s.
Vật nặng của một con lắc lò xo di chuyển lên xuống sau khi được kích thích dao động tại thời điểm \[t = 0\]. Đồ thị biểu diễn li độ của vật nặng theo thời gian được cho như hình vẽ.
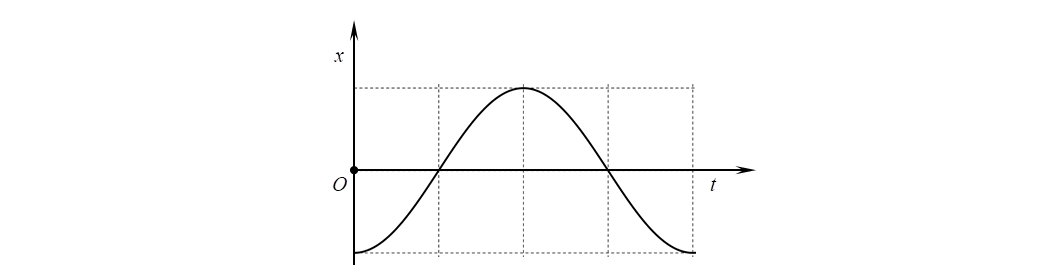
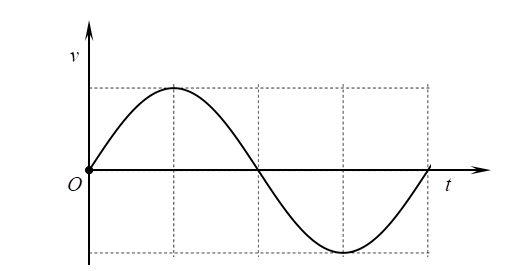
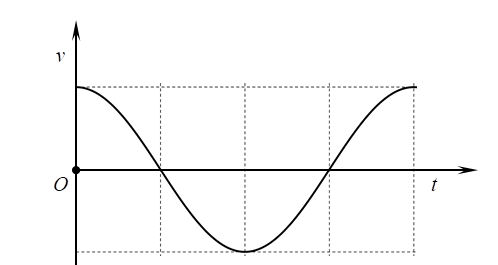
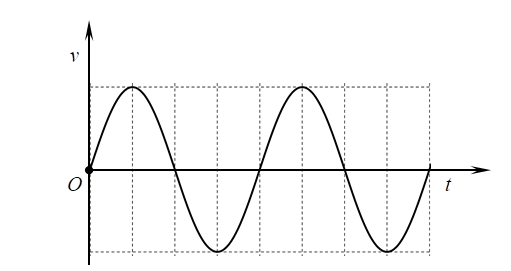
Đồ thị nào sau đây biểu diễn đúng vận tốc của vật theo thời gian?
 |  |
Hình A | Hình B |
 Hình C Hình C |  Hình D Hình D |
Hình A.
Hình B.
Hình C.
Hình D.
Một chất điểm dao động điều hoà theo phương trình \[x = 2\cos \left( {2\pi t} \right)\](\[x\] tính bằng cm; \[t\] tính bằng s). Tại thời điểm \[t = \frac{1}{3}\]s chất điểm có vận tốc bằng
\[ - 2\pi \]cm/s.
\[2\pi \sqrt 3\] cm/s
\[2\pi \]cm/s.
\[2\pi \sqrt 3 \]cm/s.
Một con lắc lò xo gồm một vật nhỏ có khối lượng \[m\] và lò xo nhẹ, dao động điều hòa dọc theo trục \[Ox\] quanh vị trí cân bằng O với tần số góc là \[\omega \]. Biểu thức lực kéo về tác dụng lên vật theo li độ \[x\] là
\[F = m\omega x\].
\[F = - m{\omega ^2}x\].
\[F = m{\omega ^2}x\].
\[F = - m\omega x\].
Một con lắc đơn có chiều dài \[\ell = 1,2\]m dao động nhỏ với tần số góc bằng 2,86 rad/s tại nơi có gia tốc trọng trường \[g\]. Giá trị của \[g\] tại đó bằng
9,82 m/s2.
9,88 m/s2.
9,85 m/s2.
9,80 m/s2.
Một chất điểm dao động điều hòa trên trục Ox, động năng Wđ của chất điểm này biến thiên với chu kì 1 s. Chu kì dao động của chất điểm này là
1 s.
2 s.
3 s.
4 s.
Một chất điểm dao động tuần hoàn với chu kì bằng 1 s. Biết quỹ đạo chuyển động của chất điểm dài 8 cm. Tính quãng đường chất điểm đi được trong 6 s.
72 cm.
48 cm.
96 cm.
108 cm
Một vật dao động điều hòa với biên độ bằng 4 cm. Khi pha của dao động bằng \[\frac{\pi }{3}\] thì li độ của vật bằng:
2 cm.
4 cm.
- 2 cm.
- 4 cm.
Dao động điều hòa đổi chiều khi
lực tác dụng có độ lớn cực đại.
lực tác dụng có độ lớn cực tiểu.
lực tác dụng biến mất.
không có lực nào tác dụng vào vật
Gia tốc của một chất điểm dao động điều hòa biến thiên
cùng tần số và cùng pha với li độ.
cùng tần số và ngược pha với li độ.
khác tần số và vuông pha với li độ.
khác tần số và cùng pha với li độ.
Một vật dao động điều hòa có biên độ \[A\] và chu kì \[T\], mốc thời gian (\[t = 0\]) là lúc vật đi qua vị trí cân bằng, phát biểu nào sau đây là sai?
Sau \[\frac{T}{2}\], vật đi được quãng đường \[2A\].
Sau \[\frac{T}{8}\], vật đi được quãng đường \[\frac{A}{2}\].
Sau \[\frac{T}{4}\], vật đi được quãng đường\[A\].
Sau \[\frac{T}{{12}}\], vật đi được quãng đường \[\frac{A}{2}\].
Một con lắc đơn dao động điều hòa với biên độ góc \({\alpha _0}\). Lấy mốc thế năng ở vị trí cân bằng. Ở vị trí con lắc có động năng bằng thế năng thì li độ góc của nó bằng:
\( \pm \frac{{{\alpha _0}}}{{2\sqrt 2 }}\).
\( \pm \frac{{{\alpha _0}}}{{2\sqrt 3 }}\).
\( \pm \frac{{{\alpha _0}}}{{\sqrt 2 }}\).
\( \pm \frac{{{\alpha _0}}}{2}\).
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Phát biểu nào đúng, phát biểu nào sai? Khi đưa một con lắc đơn lên cao theo phương thẳng đứng (coi chiều dài của con lắc không đổi).
a) tần số dao động điều hoà của nó sẽ giảm vì gia tốc trọng trường giảm theo độ cao.
b) chu kỳ dao động điều hoà của nó giảm.
c) gia tốc trọng trường giảm.
d) tăng vì tần số dao động điều hoà của nó tỉ lệ nghịch với gia tốc trọng trường.
Phát biểu nào đúng, phát biểu nào sai khi nói về dao động cưỡng bức?
a) Dao động cưỡng bức có biên độ không đổi.
b) Tần số của dao động cưỡng bức bằng tần số của lực cưỡng bức.
c) Dao động chịu tác dụng của một ngoại lực cưỡng bức tuần hoàn gọi là dao động cưỡng bức.
d) Biên độ của dao động cưỡng bức giảm dần theo thời gian.
Phát biểu nào đúng, phát biểu nào sai? Một vật dao động điều hòa theo một trục cố định (mốc thế năng ở vị trí cân bằng) thì
a) khi ở vị trí cân bằng, động năng của vật bằng cơ năng.
b) khi vật đi từ vị trí cân bằng ra biên, vận tốc và gia tốc của vật luôn cùng dấu.
c) động năng của vật cực đại khi gia tốc của vật có độ lớn cực đại.
d) thế năng của vật cực đại khi vật ở vị trí biên.
Phát biểu nào đúng, phát biểu nào sai? Một vật dao động điều hòa khi đang chuyển động từ vị trí cân bằng đến vị trí biên âm thì
a) vận tốc và gia tốc cùng có giá trị dương.
b) độ lớn vận tốc và độ lớn gia tốc cùng giảm.
c) vectơ vận tốc ngược chiều với vectơ gia tốc.
d) độ lớn vận tốc tăng và độ lớn gia tốc không thay đổi.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là \(40\sqrt 3 \,\,cm/{s^2}\) . Biên độ dao động của chất điểm là bao nhiêu? (Đơn vị: cm).
Một vật dao động theo phương trình \[x = 4cos\left( {\frac{{\pi t}}{6}} \right)\left( {cm} \right)\] (t đo bằng giây). Tại thời điểm t1 li độ là \(2\sqrt 3 \)cm và đang giảm. Tính li độ sau thời điểm t1 là 3 (s). (Đơn vị: cm).
Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, dao động điều hoà. Nếu vật có khối lượng 200 g thì chu kì dao động của con lắc là 2 s. Để chu kì con lắc là 1 s thì khối lượng m bằng bao nhiêu? (Đơn vị: gam).
Một lò xo dãn ra \[2,5{\rm{ }}cm\]khi treo vào nó một vật có khối lượng 250 g. Chu kì của con lắc được tạo thành như vậy là bao nhiêu? Cho \[g = 10\,m/{s^2}\]. (Đơn vị: giây).
Một con lắc lò xo có cơ năng \[W{\rm{ }} = {\rm{ }}0,9{\rm{ }}J\]và biên độ dao động A = 15 cm. Hỏi động năng của con lắc tại vị trí có li độ \[x = - 5{\rm{ }}(cm)\] là bao nhiêu? (Đơn vị: J).
Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad ở một nơi có gia tốc trọng trường g = 10 m/s2. Vào thời điểm ban đầu vật đi qua vị trí có li độ dài 8 cm và có vận tốc \(20\sqrt 3 \) cm/s. Tốc độ cực đại của vật dao động là bao nhiêu? (Đơn vị: m/s).





