ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Giá trị lớn nhất, nhỏ nhất của hàm số
28 câu hỏi
Cho biết GTLN của hàm số f(x) trên \[\left[ {1;3} \right]\;\]là M=−2. Chọn khẳng định đúng:
A.
\[f\left( 1 \right) = f\left( 3 \right) = - 2\]
\[f\left( x \right) < - 2,\forall x \in \left[ {1;3} \right]\]
D.
Cho hàm số f(x) xác định trên \[\left[ {0;2} \right]\;\]và có GTNN trên đoạn đó bằng 5. Chọn kết luận đúng:
\[f\left( 0 \right) < 5\]
B.
\[f\left( 1 \right) = 5\]
\[f\left( 0 \right) = 5\]
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=sinx trên đoạn \[[ - \frac{\pi }{2}; - \frac{\pi }{3}]\] lần lượt là
\[ - \frac{1}{2}; - \frac{{\sqrt 3 }}{2}\]
\[ - \frac{{\sqrt 3 }}{2}; - 1\]
\[ - \frac{{\sqrt 3 }}{2}; - 2\]
\[ - \frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 3 }}{2}\]
Giá trị nhỏ nhất của hàm số \[y = 2x + \cos x\] trên đoạn \[\left[ {0;1} \right]\;\]là :
−1
1
π
0
Cho hàm số f(x) xác định và liên tục trên R, có \[\mathop {\lim }\limits_{x \to + \infty } = + \infty ;\mathop {\lim }\limits_{x \to - \infty } = - \infty \] , khi đó:
Hàm số đạt GTNN tại x=0.
Hàm số đạt GTLN tại x=0.
Hàm số đạt GTNN tại \[x = - \infty .\]
Hàm số không có GTLN và GTNN trên R.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, chọn kết luận đúng:
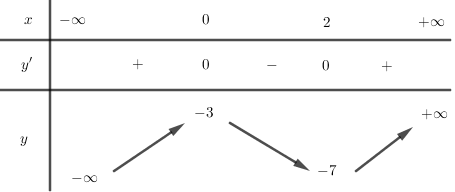
\[\mathop {\max }\limits_{\left[ { - 3;0} \right]} f\left( x \right) = f\left( { - 3} \right)\]
\[\mathop {\min }\limits_{\left[ {1;3} \right]} f\left( x \right) = - 7\]
\[\mathop {\min }\limits_{\left( { - \infty ;2} \right]} f\left( x \right) = - 7\]
\[\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) < - 3\]
Cho hàm số y=f(x) có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
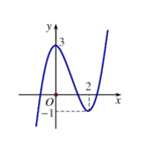
\[\mathop {\max }\limits_{x \in \mathbb{R}} f\left( x \right) = 3\]
Hàm số đồng biến trên khoảng \[\left( { - \infty ;3} \right)\]
Giá trị cực tiểu của hàm số bằng 2
\[\mathop {\min }\limits_{x \in \left[ {0;4} \right]} f\left( x \right) = - 1\]
Cho hàm số y=f(x) có bảng biến thiên như sau:
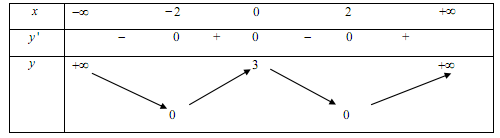
Khẳng định nào sau đây là khẳng định đúng?
Hàm số đạt cực đại tại x=3
GTNN của hàm số bằng giá trị cực tiểu của hàm số.
Hàm số không có GTNN.
Hàm số có GTLN là 3.
Cho hàm số y=f(x)) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn \[\left[ { - 2;2} \right]\]
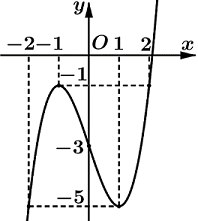
m=−5,M=−1.
m=−1,M=0.
m=−2,M=2.
m=−5,M=0.
Đề thi THPT QG - 2021 - mã 101
Trên đoạn \[\left[ {0;3} \right],\]hàm số \[y = - {x^3} + 3x\;\] đạt giá trị lớn nhất tại điểm
x=0.
x=3.
x=1.
x=2.
Tìm giá trị lớn nhất của hàm số \[y = {x^3} - 5{{\rm{x}}^2} + 3{\rm{x}} - 1\] trên đoạn \[\left[ {2;4} \right]\]
M=−10
M=−7
M=−5
M=1
Giá trị lớn nhất của hàm số \[f\left( {\rm{x}} \right) = \frac{{6 - 8{\rm{x}}}}{{{x^2} + 1}}\] trên tập xác định của nó là:
−2
\(\frac{2}{3}\)
8
10
Gọi giá trị lớn nhất và nhỏ nhất của hàm số \[y = {x^4} + 2{x^2} - 1\;\] trên đoạn \[\left[ { - 1;2} \right]\;\]lần lượt là M và m. Khi đó giá trị của M.m là:
−2
46
−23
23
Cho hàm số \[y = x + \frac{1}{x}.\] Giá trị nhỏ nhất của hàm số trên khoảng \[\left( {0; + \infty } \right)\;\]là:
2
−3
5
10
Cho hàm số \[y = {x^3} - 3m{x^2} + 6\], giá trị nhỏ nhất của hàm số trên \[\left[ {0;3} \right]\;\]bằng 2 khi:
\[m = 2\]
\[m = \frac{{31}}{{27}}\]
\[m > \frac{3}{2}\]
\[m = 1\]
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Gọi a,A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của f(x+1) trên đoạn \[\left[ { - 1;0} \right].\;\]Giá trị a+A bằng:
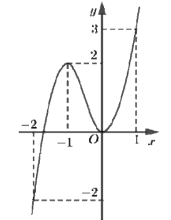
−1
2
0
3
Cho hàm số y=f(x) liên tục trên đoạn \[\left[ { - 1;4} \right]\;\]và có đồ thị như hình vẽ
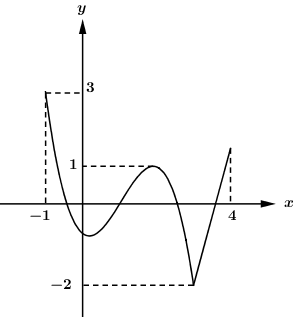
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn \[\left[ { - 10;10} \right]\;\]để bất phương trình \[|f(x) + m| < 2m\;\]đúng với mọi x thuộc đoạn \[\left[ { - 1;4} \right]?\]
6
5
7
8
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) có đồ thị \[y = f\prime (x)\;\] như hình vẽ. Đặt \[g(x) = 2f(x) - {x^2}\]. Khi đó giá trị lớn nhất của hàm số g(x) trên đoạn \[\left[ { - 2;4} \right]\;\]là:
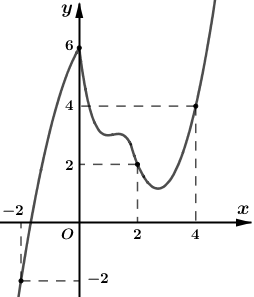
g(−2).
g(2).
g(4).
g(0).
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Xét hàm số \[g\left( x \right) = f({x^3} + 2x) + m\]. Giá trị của tham số m để giá trị lớn nhất của hàm số g(x) trên đoạn \[\left[ {0;1} \right]\;\]bằng 9 là:
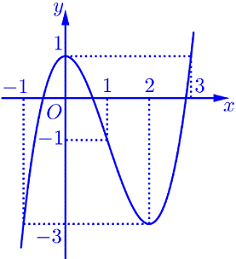
m=10
m=6
m=12
m=8
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f(1 - 2cosx)\] trên \[\left[ {0;\frac{{3\pi }}{2}} \right].\]Giá trị của M+m bằng
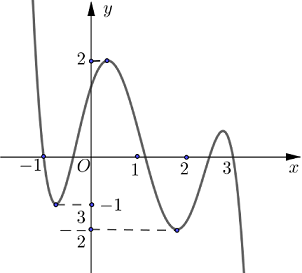
\(\frac{1}{2}\)
\(\frac{3}{2}\)
2
1
Có bao nhiêu số nguyên \[m \in [ - 5;5]\;\] để \[\mathop {min}\limits_{\left[ {1;3} \right]} \mid {x^3} - 3{x^2} + m\mid \ge 2.\]
6
4
3
5
Cho f(x) mà đồ thị hàm số \[y = f\prime (x)\;\] như hình vẽ bên
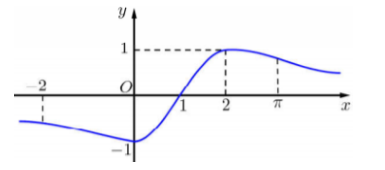
\[m < f\left( 0 \right)\]
\[m < f\left( 1 \right) - 1\]
\[m < f\left( { - 1} \right) + 1\]
\[m < f\left( 2 \right)\]
Cho \[f\left( x \right) = \frac{1}{{{x^2} - 4x + 5}} - \frac{{{x^2}}}{4} + x\] Gọi \[M = \mathop {Max}\limits_{x \in \left[ {0;3} \right]} f(x);\;m = \mathop {Min}\limits_{x \in \left[ {0;3} \right]} f\left( x \right)\] Khi đó M−m bằng:
1.
\[\frac{3}{5}.\]
\[\frac{7}{5}.\]
\[\frac{9}{5}.\]
Cho hàm số f(x). Biết hàm số f′(x) có đồ thị như hình dưới đây. Trên đoạn \[\left[ { - 4;3} \right],\]hàm số \[g(x) = 2f(x) + {(1 - x)^2}\;\] đạt giá trị nhỏ nhất tại điểm
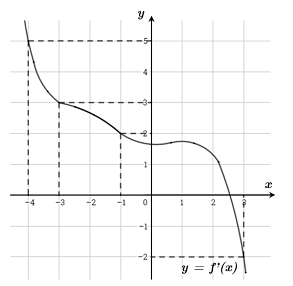
x=−1.
x=−4.
x=−3.
x=3.
Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] có đồ thị như hình bên:
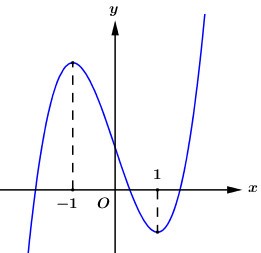
Giá trị nguyên lớn nhất của tham số m để hàm số \[y = f(|x| - m)\;\] đồng biến trên khoảng \[\left( {10; + \infty } \right)\;\]là:
−10
10
9
-11
Cho các số thực x,y thay đổi thỏa mãn \[{x^2} + 2{y^2} + 2xy = 1\] và hàm số \[f(t) = {t^4} - {t^2} + 2\]. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \[Q = f\left( {\frac{{x + y + 1}}{{x + 2y - 2}}} \right)\] Tính M+m?
\[8\sqrt 3 - 2\]
\[\frac{{303}}{2}\]
\[\frac{{303}}{4}\]
\(4\sqrt 3 + 2\)
Người ta cần chế tạo các món quà lưu niệm bằng đồng có dạng khối chóp tứ giác đều, được mạ vàng bốn mặt bên và có thể tích bằng 16cm3. Diện tích mạ vàng nhỏ nhất của khối chóp bằng bao nhiêu cm2? (Kết quả làm tròn đến hàng đơn vị.)
Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích V=6m3 dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông cốt thép. Phần nắp bể để hở một khoảng hình vuông có diện tích bằng \(\frac{2}{9}\) diện tích nắp bể. Biết rằng chi phí cho 1m2 bê tông cốt thép là 1.000.000d. Tính chi phí thấp nhất mà cô Ngọc phải trả khi xây bể (làm tròn đến hàng trăm nghìn và các chữ số viết liền)?



