22 câu hỏi
Số điểm chung của đường thẳng và mặt phẳng không thể là:
chỉ hai điểm
một điểm
không có điểm nào
vô số điểm
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng
song song
cắt nhau
chéo nhau
trùng nhau
Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là:
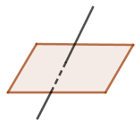
0
1
2
vô số
Cho tứ diện ABCD. Chọn kết luận đúng:
\[AD \subset \left( {ABC} \right)\]
\[AD \cap \left( {ABC} \right) = C\]
\[AB \subset \left( {ABC} \right)\]
\[AC//\left( {ABD} \right)\]
Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì:
\[d//(\alpha )\;\]
d cắt \[\left( \alpha \right)\;\]
\[d \subset \left( \alpha \right)\]
\[d \supset \left( \alpha \right)\]
Nếu đường thẳng \[d//\left( \alpha \right)\;\] và \[d\prime \subset (\alpha )\;\] thì d và d′ có thể:
song song
chéo nhau
cắt nhau
song song hoặc chéo nhau
Cho đường thẳng d song song với mặt phẳng (α), nếu mặt phẳng (β) chứa d mà cắt (α) theo giao tuyến d′ thì:
\[d \equiv d'\]
\[d//d'\]
\[d//\left( \beta \right)\]
\[d'//\left( \alpha \right)\]
Cho hai đường thẳng chéo nhau, số mặt phẳng chứa đường thẳng này mà song song đường thẳng kia có thể là:
1
2
vô số
0
Cho tứ diện ABCD, gọi G là trọng tâm tam giác ACD, M thuộc đoạn thẳng BC sao cho CM=2MB. Chọn mệnh đề đúng trong các mệnh đề sau?
MG//(ABC)
MG//(ABD)
MG//CD
MG//BD
Cho hình chóp S.ABCD. Gọi M,N lần lượt là trọng tâm của tam giác SAB và ABC.ABC. Khi đó MN song song với
mp(SAD)
AD
mp(SCD)
mp(SBD)
Hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O và O′ lần lượt là tâm hình bình hành ABCD và ABEF. OO′ song song với:
mp(DCEF)
mp(ADF)
mp(BCE)
Cả A, B, C
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q, lần lượt là các điểm nằm trên các cạnh BC,SC,SD,AD sao cho MN//BS,NP//CD,MQ//CD. Hỏi PQ song song với mặt phẳng nào sau đây?
mp(SBC)
mp(SAB)
mp(SAD)
mp(SCD)
Mệnh đề nào dưới đây đúng?
Hai đường thẳng cùng song song với một mặt phẳng thì hai đường thẳng đó song song với nhau
Hai đường thẳng phân biệt cùng song song với một đường thẳng thì cắt nhau
Hai đường thẳng phân biệt cùng song song với một đường thẳng thì song song với nhau
Hai đường thẳng cùng song song với một mặt phẳng thì hai đường thẳng đó trùng nhau.
Cho các mệnh đề sau:
Số mệnh đề đúng là:
Nếu a//(P)) thì aa song song với mọi đường thẳng nằm trong (P).
Nếu a//(P) thì aa song song với một đường thẳng nào đó nằm trong (P).
Nếu a//(P) thì có vô số đường thẳng nằm trong (P) và song song với a
Nếu a//(P) thì có một đường thẳng dd nào đó nằm trong (P) sao cho a và d đồng phẳng.
1
2
3
4
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Xét các khẳng định sau:
(1) MN // (SCD)
(2) EF // (SAD)
(3) NE // (SAC)
(3) IJ // (SAB)
Có bao nhiêu khẳng định đúng?
1
2
3
4
Cho đường thẳng a song song với mặt phẳng (P). Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a có thể là:
0
1
2
Vô số
Cho tứ diện ABCD. Gọi \[{G_1},{G_2}\;\] lần lượt là trọng tâm các tam giác BCD và ACD. Chọn câu sai ?
\[{G_1}{G_2}//(ABD)\]
\[{G_1}{G_2}//(ABC)\]
\[B{G_1};A{G_2};CD\] đồng quy
\[{G_1}{G_2} = \frac{2}{3}AB\]
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mp(α) qua BD và song song với SA cắt SC tại K. Chọn khẳng định đúng?
SK=2KC
SK=3KC
SK=KC
\[SK = \frac{1}{2}KC\]
Cho tứ diện đều SABC. Gọi I là trung điểm của AB,M là một điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với SI,IC, biết AM=x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là:
\[3x\left( {1 + \sqrt 3 } \right)\]
\[2x\left( {1 + \sqrt 3 } \right)\]
\[x\left( {1 + \sqrt 3 } \right)\]
Không xác định
Cho tứ diện ABCD, M là trung điểm của cạnh CD, G là trọng tâm tứ diện. Khi đó 2 đường thẳng AD và GM là hai đường thẳng:
Chéo nhau
có hai điểm chung
song song
có một điểm chung
Cho hình chóp S.ABC, M là một điểm nằm trong tam giác ABC. Các đường thẳng qua MM và song song với SA,SB,SC cắt các mặt (SBC),(SAC),(SAB) lần lượt tại A′,B′,C′. \[\frac{{MA'}}{{SA}} + \frac{{MB'}}{{SB}} + \frac{{MC'}}{{SC}}\] có giá trị không đổi bằng bao nhiêu khi M di động trong tam giác ABC?
\[\frac{1}{3}\]
\(\frac{1}{2}\)
1
\[\frac{2}{3}\]
Cho tứ diện ABCD có AB=CD=4,BC=AD=5,AC=BD=6. M là điểm thay đổi trong tâm giác ABC. Các đường thẳng qua M song song với AD,BD,CD tương ứng cắt mặt phẳng (BCD),(ACD),(ABD) tại A′,B′,C′. Giá trị lớn nhất của MA′.MB′.MC′ là
\[\frac{{40}}{9}\]
\[\frac{{24}}{9}\]
\[\frac{{30}}{9}\]
\[\frac{{20}}{9}\]
