ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Dấu của tam thức bậc hai
18 câu hỏi
Cho \[f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right).\] Điều kiện để f(x) >0\[,\forall x \in R\] là
\(\left\{ {\begin{array}{*{20}{c}}{a >0}\\{\Delta \le 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{a >0}\\{\Delta \ge 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{a >0}\\{\Delta < 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{\Delta >0}\end{array}} \right.\)
Cho \[f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\]. Điều kiện để \[f\left( x \right) \le 0,\forall x \in R\;\] là
\(\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{\Delta \le 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{\Delta \ge 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{a >0}\\{\Delta < 0}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{\Delta >0}\end{array}} \right.\)</>
Cho \[f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\] có \[\Delta = {b^2} - 4ac < 0\]. Khi đó mệnh đề nào đúng?
\[f\left( x \right) >0\,,\forall x \in \mathbb{R}\]
\[f\left( x \right) < 0\,,\forall x \in \mathbb{R}\]
f(x) không đổi dấu
Tồn tại x để f(x) = 0
Tam thức bậc hai \[f\left( x \right) = 2{x^2} + 2x + 5\] nhận giá trị dương khi và chỉ khi
\[x \in \left( {0; + \infty } \right).\]
\[x \in \left( { - 2; + \infty } \right).\]
\[\forall x \in \mathbb{R}.\]
\[x \in \left( { - \infty ;2} \right).\]Trả lời:
Cho các tam thức \[f\left( x \right) = 2{x^2} - 3x + 4;\,g\left( x \right) = - {x^2} + 3x - 4;\,h\left( x \right) = 4 - 3{x^2}\]. Số tam thức đổi dấu trên RR là:
0
1
2
3
Tam thức bậc hai \[f\left( x \right) = {x^2} + \left( {1 - \sqrt 3 } \right)x - 8 - 5\sqrt 3 \]:
Dương với mọi \[x \in \mathbb{R}\].
Âm với mọi \[x \in \mathbb{R}\].
Âm với mọi \[x \in \left( { - 2 - \sqrt 3 ;1 + 2\sqrt 3 } \right)\]
Âm với mọi \[x \in \left( { - \infty ;1} \right)\]
Bảng xét dấu nào sau đây là của tam thức \[f\left( x \right) = \;{x^2} + 12x + 36\]?
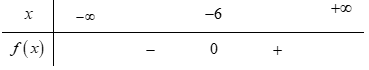
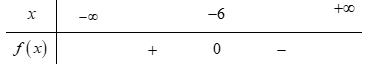
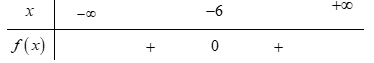
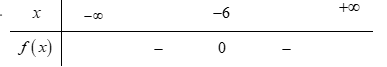
Cho tam thức bậc hai \[f\left( x \right) = {x^2} - bx + 3\]. Với giá trị nào của bb thì tam thức f(x) có hai nghiệm phân biệt?
\[b \in \left[ { - 2\sqrt 3 ;2\sqrt 3 } \right]\]
\[b \in \left( { - 2\sqrt 3 ;2\sqrt 3 } \right)\]
\[b \in \left( { - \infty ; - 2\sqrt 3 } \right] \cup \left[ {2\sqrt 3 ; + \infty } \right)\]
Giá trị nào của m thì phương trình \[(m - 3){x^2} + (m + 3)x - (m + 1) = 0\;\left( 1 \right)\]có hai nghiệm phân biệt?
\[m \in \left( { - \infty ; - \frac{3}{5}} \right) \cup \left( {1; + \infty } \right) \setminus \left\{ 3 \right\}\]
\[m \in \left( { - \frac{3}{5};1} \right)\]
\[m \in \left( { - \frac{3}{5}; + \infty } \right)\]
\[m \in \mathbb{R} \setminus \left\{ 3 \right\}\]
Các giá trị m để tam thức \[f\left( x \right) = {x^2} - \left( {m + 2} \right)x + 8m + 1\;\] đổi dấu 2 lần là
\[m \le 0\;\] hoặc \[m \ge 28\].
m < 0 hoặc m >28.
0< m < 28 .
m >0.
Tìm tập xác định D của hàm số \[y = \sqrt {\frac{{{x^2} + 5x + 4}}{{2{x^2} + 3x + 1}}} \] là
\[{\rm{D}} = \left[ { - 4; - 1} \right) \cup \left( { - \frac{1}{2}; + \infty } \right).\]
\[{\rm{D}} = \left( { - \infty ; - 4} \right] \cup \left( { - 1; - \frac{1}{2}} \right).\]
\[{\rm{D}} = \left( { - \infty ; - 4} \right] \cup \left( { - \frac{1}{2}; + \infty } \right).\]
\[{\rm{D}} = \left[ { - 4; - \frac{1}{2}} \right).\]
Tập nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 4x + 3 >0}\\{{x^2} - 6x + 8 >0}\end{array}} \right.\) là
\[\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\]
\[\left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\]
\[\left( { - \infty ;2} \right) \cup \left( {3; + \infty } \right)\]
\[\left( {1;4} \right)\]
Tìm m để \[(m + 1){x^2} + mx + m < 0,\forall x \in \mathbb{R}\]?
m < −1.
m >−1.
\[m < - \frac{4}{3}\]
\[m >\frac{4}{3}\]
Với giá trị nào của a thì bất phương trình \[a{x^2} - x + a \ge 0\;\] nghiệm đúng với \[\forall x \in \mathbb{R}\;\]?
a = 0.
a < 0
\[0 < a \le \frac{1}{2}\]
\[a \ge \frac{1}{2}\]
Với giá trị nào của m thì bất phương trình \[{x^2} - x + m \le 0\] vô nghiệm?
m<1.
m>1.
\[m < \frac{1}{4}\]
\[m >\frac{1}{4}\]
Tìm tất cả giá trị thực của tham số mm để hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} + 10x + 16 \le 0\,\,\,\left( 1 \right)}\\{mx \ge 3m + 1\,\,\,\left( 2 \right)}\end{array}} \right.\) vô nghiệm.
Bất phương trình \[\left( 1 \right) \Leftrightarrow - 8 \le x \le - 2.\] Suy ra\[{S_1} = \left[ { - 8; - 2} \right]\]
\[m >- \frac{1}{5}.\]
\[m >\frac{1}{4}.\]
\[m >- \frac{1}{{11}}.\]
\[m >\frac{1}{{32}}.\]
Có bao nhiêu giá trị m nguyên âm để mọi x >0 đều thoả bất phương trình \[{\left( {{x^2} + x + m} \right)^2} \ge {\left( {{x^2} - 3x - m} \right)^2}\]?
0.
1.
2.
3.
Với giá trị nào của m thì phương trình \[m{x^2} - 2(m - 2)x + 3 - m = 0\;\] có hai nghiệm trái dấu?
0 < m < 3
m < 0
m < 0 hoặc m >3
m >3


