Đề thi thử Toán THPT chuyên KHTN Hà Nội (lần 01) năm 2025-2026 có đáp án
22 câu hỏi
Trong không gian \[(Oxyz)\], điểm nào sau đây thuộc đường thẳng \[(d):\frac{{x - 1}}{1} = \frac{{y - 1}}{1} = \frac{{z - 3}}{2}\]?
\[M( - 1; - 1; - 3)\].
\[N(1;1;2)\].
\[P( - 1; - 1; - 2)\].
\[Q(1;1;3)\].
Nghiệm của phương trình \[{2^{x + 1}} = 16\]
\[x = 9\].
\[x = 5\].
\[x = 3\].
\[x = 7\] .
Cho hàm số\[f(x)\] có bảng biến thiên như sau
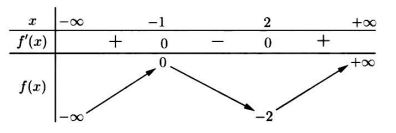
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\[( - 2;0)\].
\[( - 1;2)\].
\[( - \infty ; - 1)\].
\[(2; + \infty )\] .
Trong không gian \[(Oxyz)\], cho hai điểm \[A(1; - 2; - 1)\,;\,B(3;4; - 3)\]. Trung điểm của đoạn thẳng \[AB\]có tọa độ là
\[(1;3;1)\].
\[(2;1; - 2)\].
\[(2;1; - 12)\].
\[(2; - 1; - 2)\].
Đồ thị hàm số \(y = \frac{{x + 2}}{{x - 2}}\) có tiệm cận ngang là
\(x = 2\).
\(x = - 2\).
\(y = 1\).
\(y = - 1\).
Hàm số nào dưới đây có đồ thị là đường cong hình bên?
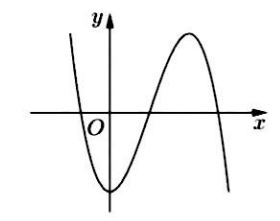
\(y = - {x^2} + 2x - 2\).
\(y = {x^2} - 2x - 2\).
\(y = - {x^3} + 3{x^2} - 2\).
\(y = {x^3} - 3{x^2} - 2\).
Trong khoảng \(\left( {0;2\pi } \right)\), phương trình \(2\sin x = 1\) có bao nhiêu nghiệm?
\(1\).
\(2\).
\(3\).
\(4\).
Trong không gian \(Oxyz\), vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng \(\left( P \right):x - y - z + 2 = 0\)?
\(\overrightarrow n = \left( {1; - 1;2} \right)\).
\(\overrightarrow n = \left( { - 1; - 1;2} \right)\).
\(\overrightarrow n = \left( {2; - 1; - 1} \right)\).
\(\overrightarrow n = \left( {1; - 1; - 1} \right)\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x + 1} \right){x^2}{\left( {x - 3} \right)^3},\forall x \in \mathbb{R}\). Hàm số đã cho có bao nhiêu điểm cực trị?
\(2\).
\(3\).
\(1\).
\(5\).
Trong không gian \(Oxyz\), cho các điểm \(A\left( {0;0;3} \right),B\left( {0;1;2} \right)\) và \(C\left( {1;3;1} \right)\). Tam giác \(ABC\) có diện tích bằng
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{{3\sqrt 3 }}{2}\).
\(\sqrt 3 \).
\(\frac{5}{2}\).
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 3x + 1\) trên đoạn \(\left[ { - 2;0} \right]\) bằng
\(1\).
\( - 2\).
\( - 1\).
\(3\).
Cho các số thực dương \(a,b,c\) thỏa mãn \({\log _a}b = 3;{\log _a}c = - 2\). Giá trị của \({\log _a}\left( {\frac{{{a^3}{b^2}}}{c}} \right)\) bằng
\(14\).
\(11\).
\(7\).
\(20\).
Một công ty thực phẩm muốn tạo ra một loại thức ăn hỗn hợp cho vật nuôi từ hai nguyên liệu chính là ngô và đậu nành. Biết rằng 1 kg ngô có \(0,1{\rm{\;kg}}\) protein và \(0,6{\rm{\;kg}}\) carbohydrate, 1 kg đậu nành có \(0,4{\rm{\;kg}}\) protein và \(0,3{\rm{\;kg}}\) carbohydrate. Công ty cần sản xuất một bao thức ăn hỗn hợp sao cho tổng khối lượng ngô và đậu lành không vượt quá 100 kg và phải đảm bảo chứa ít nhất 20 kg protein và ít nhất \(46,5{\rm{\;kg}}\) carbohydrate. Giá thành mỗi kg ngô là 5 nghìn đồng và mỗi kg đậu nành là 9 nghìn đồng. Hỏi chi phí sản xuất một bao thức ăn của công ty thấp nhất là bao nhiêu nghìn đồng?
Cường độ một trận động đất \(M\) độ Richter được cho bởi công thức \(M = {\rm{log}}A - {\rm{log}}{A_0}\) với \(A\) là biên độ rung chấn tối đa và \({A_0}\) là một biên độ chuẩn (hằng số). Ngày \(11/3/2011\) một trận siêu động đất xảy ra tại vùng Tohoku, Nhật Bản có cường độ 9,1 độ Richter. Trước đó, vào ngày \(21/5/2003\) trận động đất khác ở phía Bắc Algeria có cường độ 6,8 độ Richter. Hỏi biên độ rung chấn tối đa của trận động đất ở vùng Tohoku, Nhật Bản gấp bao nhiêu lần biên độ rung chấn tối đa của trận động đất ở phía Bắc Algeria? (kết quả làm tròn đến hàng đơn vị).
Một nhà máy sản xuất và bán \[x\] sản phẩm trong mỗi tháng. Chi phí sản xuất \[x\] sản phẩm được cho bởi công thức \[C = 10000 + 600{\rm{x}} - 0,6{{\rm{x}}^2} + 0,004{{\rm{x}}^3}\] (nghìn đồng). Biết giá bán của mỗi sản phẩm là \[p = 1800 - 6{\rm{x}}\] (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?
100
Trong không gian \[Oxyz,\] cho điểm \(A(1;1; - 1)\) và đường thẳng \(d:\frac{{x - 4}}{2} = \frac{{y - 4}}{2} = \frac{{z - 2}}{{ - 1}}.\) Gọi \[H(a;b;c)\] là hình chiếu vuông góc của điểm \(A\) trên đường thẳng \(d.\) Tính tổng \(a + b + c.\)
7
Sau khi một bệnh nhân uống một liều thuốc, nồng độ của thuốc trong máu người đó được mô hình hóa bởi hàm số \(C\left( t \right) = \frac{{120t}}{{{t^2} + 36}}\) (đơn vị: \({\rm{mg/L}}\)), trong đó \(t\) là thời gian sau khi uống thuốc (đơn vị: giờ) và \(t \ge 0\). Tìm nồng độ thuốc tối đa (đơn vị: \({\rm{mg/L}}\)) trong máu của bệnh nhân.
Trong không gian \[{\rm{Oxyz}}\] , cho hai điểm \[{\rm{A}}\left( {{\rm{2;0; - 1}}} \right)\], \[B\left( {{\rm{ - 1; - 6;7}}} \right)\] và mặt phẳng\[\left( P \right):x - y + z - 3 = 0\]. Xét điểm \[{\rm{M}}\] thuộc mặt phẳng \[\left( P \right)\]. Tìm giá trị nhỏ nhất của \[2M{A^2} + M{B^2}\].
63
Một công ty sau khi ra mắt sản phẩm mới đã ghi nhận lợi nhuận \(P\left( t \right)\) (đơn vị: tỷ đồng) sau \(t\) tháng kinh doanh. Trong năm đầu tiên, giả sử mối liên hệ giữa lợi nhuận và thời gian kinh doanh được mô hình hóa bởi hàm số:
\(P\left( t \right) = - {t^3} + 12{t^2} + 60t - 50\), \(0 \le t \le 12\).
Lợi nhuận của công ty tại thời điểm \(t = 2\) là \(110\) tỷ đồng.
Hàm số biểu thị tốc độ tăng trưởng lợi nhuận \(P'\left( t \right) = - 3{t^2} + 24t + 10\).
Lợi nhuận của công ty đạt mức tối đa tại thời điểm \(t = 10\).
Tại thời điểm \(t = 4\) thì tốc độ tăng trưởng lợi nhuận là lớn nhất.
Cho hàm số \(f\left( x \right) = {\log _2}\left( {{x^2} - 4x + 8} \right)\)
Tập xác định của hàm số \(f\left( x \right)\) là \(D = \mathbb{R}\).
Đạo hàm \(f'\left( x \right) = \frac{{2x - 4}}{{{x^2} - 4x + 8}}\).
Giá trị nhỏ nhất của hàm số trên \(R\) bằng 1.
Phương trình \(f\left( x \right) = 2025\) có đúng hai nghiệm.
Cho hàm số \(y = \frac{{2{x^2} - x + 2}}{{x - 1}}\) có đồ thị \(\left( C \right)\).
Tập xác định của hàm số đã cho là \(D = \left( {1\,;\, + \infty } \right)\).
Hàm số đã cho có đúng hai điểm cực trị.
Đồ thị \(\left( C \right)\) có tiệm cận xiên là \(y = 2x + 1\).
Xét điểm \(A\) thuộc \(\left( C \right)\), tổng khoảng cách từ \(A\) đến hai đường tiệm cận của \(\left( C \right)\) luôn lớn hơn \(2,3\).
Trong không gian \(Oxyz\) (đơn vị mỗi trục tọa độ là km). Một trạm phát sóng được đặt tại vị trí \(A(0;1;3)\) và có vùng phủ sóng là hình cầu bán kính 5 km. Một con đường thẳng được mô hình hóa bởi đường thẳng \(d:\frac{{x - 1}}{1} = \frac{y}{{ - 1}} = \frac{z}{2}\).
Vectơ \(\overrightarrow u = (1;1;2)\) là vectơ chỉ phương của đường thẳng \(d\).
Mặt cầu tâm \(A(0;1;3)\), bán kính \(R = 5\) có phương trình là \({x^2} + {(y - 1)^2} + {(z - 3)^2} = 25\).
Gọi \(H\)là hình chiếu vuông góc của \(A\)lên \(d\). Điểm \(H\)có hoành độ bằng \( - \frac{2}{3}\).
Đoạn đường nằm trong vùng phủ sóng dài 8,16 km. (Kết quả làm tròn đến hàng phần trăm).

