Đề thi thử Toán THPT Chuyên Bắc Ninh (lần 01) năm 2025-2026 có đáp án
22 câu hỏi
Cho hàm số \[y = \frac{{2x - 1}}{{x + 1}}\]. Giá trị \[f'\left( 3 \right)\] bằng
\[\frac{4}{5}\].
\[\frac{3}{{16}}\].
\[\frac{2}{9}\].
\[\frac{1}{6}\].
Cho hình lập phương\[ABCD.A'B'C'D'\]. Vectơ nào dưới đây bằng vectơ \[\overrightarrow {AD} \]?
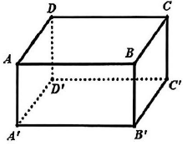
\[\overrightarrow {BC'} \].
\[\overrightarrow {DC} \].
\[\overrightarrow {B'C'} \].
\[\overrightarrow {AB} \].
Tập xác định của hàm số \[y = {\left( {x - 1} \right)^{\frac{1}{6}}} + \log \left( {4 - {x^2}} \right)\] là
\[\left[ {1;2} \right)\].
\[\left( { - 2;2} \right)\].
\[\left( {1;2} \right]\].
\[\left( {1;2} \right)\].
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm như sau:
Trung vị của mẫu số liệu trên gần với số nào nhất?
\[41,23\].
\[51,54\].
\[40,55\].
\[50,44\].
Cho hàm số \(y = - {x^3} + 3{x^2} + 9x - 1\). Hệ số góc lớn nhất của tiếp tuyến với đồ thị hàm số là
9.
12.
6.
8.
Giá trị của giới hạn \({\rm{lim}}\left( {\sqrt[3]{{{n^3} - 2{n^2}}} - n} \right)\) bằng
\(\frac{1}{3}\).
\( - \frac{2}{3}\).
1.
0.
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Gọi \({O_1},{O_2}\) lần lượt là tâm của \(ABCD\,,\,ABEF\). \(M\) là trung điểm của \(CD\). Chọn khẳng định sai trong các khẳng định sau
\(M{O_2}\) cắt \(\left( {BEC} \right)\).
\({O_1}{O_2}\) song song với \(\left( {AFD} \right)\).
\({O_1}{O_2}\) song song với \(\left( {BEC} \right)\).
\({O_1}{O_2}\) song song với \(\left( {EFM} \right)\).
Tập giá trị của hàm số \(y = {\rm{cot}}x\) là
\(\left( { - 1;1} \right)\).
\(\left[ { - 1;1} \right]\).
\(\mathbb{R}\).
\(\left( { - \infty ;0} \right)\).
Cho tứ diện \[ABCD\]. Gọi \[G\]là trọng tâm tam giác \[ABC\]. Phát biểu nào sau đây là sai?
\[\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 3\overrightarrow {DG} \].
\[\overrightarrow {GD} - \overrightarrow {GA} = \overrightarrow {AD} \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \].
Cho lăng trụ \[ABCD.A'B'C'D'\]. Có hai đáy là các hình nình hành. Các điểm \[M,N,P\] lần lượt là trung điểm của các cạnh \[AD,\,BC,\,CC'\] (tham khảo hình vẽ). Xét các khẳng định sau:
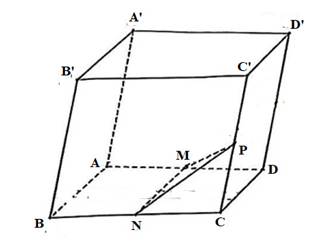
a) Mặt phẳng \[\left( {MNP} \right)\] cắt \[A'D'\].
b) Mặt phẳng \[\left( {MNP} \right)\] cắt \[DD'\] tại trung điểm của \[DD'\].
c) Mặt phẳng \[\left( {MNP} \right)\] song song với mặt phẳng \[\left( {ABC'D'} \right)\] .
Trong các khẳng định trên, số khẳng định đúng là:
0.
1.
3.
2.
Tìm số hạng tổng quát của cấp số nhân lùi vô hạn khi có tổng bằng 3 và công bội bằng \[\frac{2}{3}\].
\[{\left( {\frac{2}{3}} \right)^{n - 1}}\].
\[{\left( {\frac{2}{3}} \right)^n}\].
\[{\left( {\frac{2}{3}} \right)^{n + 1}}\].
\[{\left( {\frac{2}{3}} \right)^{n + 2}}\].
Cho hàm số đa thức bậc ba \[y = a{x^3} + b{x^2} + cx + d,\,\,\left( {a \ne 0} \right)\]có đồ thị như hình vẽ.
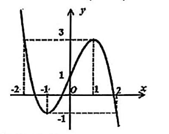
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\[\left( { - 2;0} \right)\].
\[\left( {0; + \infty } \right)\].
\[\left( { - 1;1} \right)\].
\[\left( {1; + \infty } \right)\].
Cho hàm số có đạo hàm trên và là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
Đồ thị hàm số \(g\left( x \right) = f\left( x \right) - \frac{1}{2}{x^2} + x + 2025\) cắt đường thẳng \(y = m\) tại bốn điểm phân biệt khi và chỉ khi \(g\left( { - 1} \right) < m < \min \left\{ {g\left( { - 3} \right);\,\,g\left( 1 \right)} \right\}.\)
Đồ thị hàm số \(h\left( x \right) = \frac{{2x + 1}}{{f'\left( x \right)}}\) có 3 đường tiệm cận.
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0; + \infty } \right).\)
Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên bằng \(\sqrt 2 a\). Gọi \(F\) là trung điểm của cạnh \(SA\).
Khoảng cách từ \(S\) đến mặt phẳng \(\left( {FCD} \right)\) bằng \(\frac{{a\sqrt {10} }}{5}\).
Độ lớn của góc giữa đường thẳng \(SA\) và mặt phẳng đáy bằng \(30^\circ \).
Thể tích của khối chóp \(S.FCD\) bằng \(\frac{{{a^3}\sqrt 3 }}{{24}}\).
Khoảng cách giữa \(AC\) và \(SB\) bằng \(\frac{{a\sqrt 6 }}{4}\).
Trong hộp có 45 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 45. Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Xét tính đúng sai của các mệnh đề sau:
Số cách lấy được cả 3 quả cầu đánh số chẵn bằng 1540.
Xác xuất để tích 3 số ghi trên 3 quả cầu là một số chia hết cho 8 bằng \(\frac{{523}}{{1290}}\).
Xác xuất để tổng 3 số ghi trên 3 quả cầu là số lẻ bằng \(\frac{1}{2}\).
Xác xuất để tổng 3 số ghi trên 3 quả cầu là số chia hết cho 4 bằng \(\frac{{323}}{{1290}}\).
Cho hàm số \[y = {\left( {9 - {x^2}} \right)^{\frac{1}{3}}} + \ln \left( {1 - x} \right)\].
Tập xác định của hàm số là khoảng \(\left( { - \infty ;1} \right)\).
Hàm số có đạo hàm \(y' = \frac{1}{{3\sqrt[3]{{{{\left( {9 - {x^2}} \right)}^2}}}}} - \frac{1}{{1 - x}}\).
Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {\frac{1}{4};\frac{1}{2}} \right]\) bằng \(\frac{1}{2}\sqrt[3]{{70}} - \ln 2\).
Cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) sao cho \(\left| {\overrightarrow a } \right| = \sqrt 2 \), \(\left| {\overrightarrow b } \right| = 2\) và hai vectơ \(\overrightarrow x = \overrightarrow a + \overrightarrow b \), \(\overrightarrow y = 2\overrightarrow a - \overrightarrow b \) vuông góc với nhau. Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) (đơn vị độ).
Tính tổng tất cả các giá trị nguyên của tham số m để hàm số \[y = \frac{{{x^2} + (m - 1)x + 3 - 2m}}{{x + m}}\] đạt cực tiểu tại \[x = - 1.\]
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\) , mặt phẳng \(\left( {ABC} \right)\)song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA;\,EB;\,EC;\,ED\) bằng nhau và cùng tạo với mặt phẳng một góc \(\alpha \).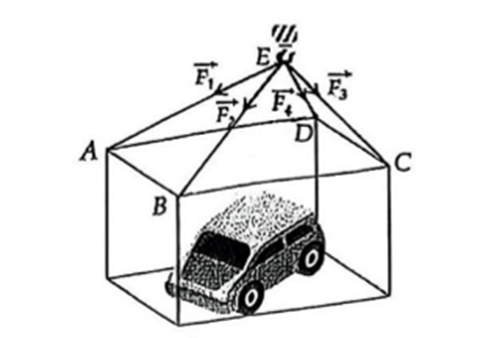
Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\,\overrightarrow {{F_3}} ;\,\overrightarrow {{F_4}} \) đều có cường độ là \(4800N\), trọng lượng của cả khung sắt chứa ô tô là \(7200\sqrt 6 N\). Tính \(\sin \alpha \) (Làm tròn kết quả đến chữ số hàng phần trăm).
Cho hình tứ diện \[ABCD\] có tất cả các cạnh bằng \[6.\] Gọi \[M,N\] lần lượt là trung điểm của \[CA,CB.\]\[P\] là điểm trên cạnh \[BD\] sao cho \[BP = 2PD.\] Gọi \[(H)\] là hình giới hạn bởi giao tuyến của mặt phẳng \[(MNP)\] với các mặt của tứ diện \[ABCD.\] Tính diện tích hình \[(H)\] (kết quả làm tròn đến hàng phần trăm).
Mội người đàn ông muốn chèo thuyền ở vị trí \[A\] tới điểm \[B\] về phía hạ lưu bờ đối diện trên một bờ sông thẳng rộng \[3\] km (như hình vẽ). Anh chèo thuyền đến một điểm \[D\] giữa \[C\] và \[B\] và sau đó chạy đến \[B\]. Biết anh ấy có thể chèo thuyền \[6\]km/h, chạy \[8\]km/h và quãng đường \[BC = 8\]km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến \[B\] là \[a + \frac{b}{c}\sqrt d \] trong đó \[a,b,c,d \in {\mathbb{N}^*}\], \[\frac{b}{c}\] là phân số tối giản và \[d\] là số nguyên tố. Giá trị của \[a + b + c + d\] bằng bao nhiêu?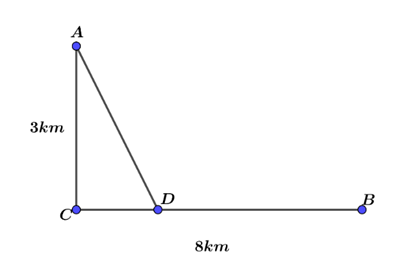 
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(2\). Hình chiếu vuông góc của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(ABC\). Biết khoảng cách giữa hai đường thẳng \(AA'\) và \[BC\] bằng \(\frac{{\sqrt 3 }}{2}\). Tính thể tích \(V\) của khối lăng trụ \(ABC.A'B'C'\) (kết quả làm tròn đến hàng phần trăm).
