Đề ôn luyện Toán theo Chủ đề 6. Vectơ và phương pháp tọa độ trong không gian (Đề số 2)

Trong không gian với hệ toạ độ \[Oxyz\], cho mặt phẳng \[\left( \alpha \right):x - 2y + 2z - 3 = 0\]. Điểm nào sau đây thuộc mặt phẳng \[\left( \alpha \right)\]?     

Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \[A\left( {1\,;0\,;2} \right)\] và \[B\left( { - 1\,;2\,;0} \right)\]. Trung điểm của đoạn thẳng \[AB\] có tọa độ là 

Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\vec m = \left( {1; - 1;1} \right)\) và \(\vec n = \left( { - 1;1; - 1} \right)\). Côsin của góc giữa hai vectơ \(\vec m\), \(\vec n\) bằng     

Trong không gian với hệ trục tọa độ \(Oxyz\), cho điểm \(M\left( {1;2; - 2} \right)\) và mặt phẳng\(\left( P \right)\) có phương trình\(2x + y - 3z + 1 = 0\). Phương trình đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) là     

Trong không gian với hệ toạ độ \(Oxyz\), cho các điểm \(A\left( {1;3;2} \right),\,B\left( {1;0;1} \right),\,C\left( {5; - 3;2} \right)\). Biết rằng \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 2m\). Giá trị của m là     

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):2x - 2y + z - 3 = 0\). Khoảng cách từ điểm \(M\left( { - 1;2;0} \right)\) đến mặt phẳng \(\left( P \right)\) bằng      

Trong không gian với hệ trục toạ độ \(Oxyz\), cho điểm \(M\left( {1; - 3;4} \right)\), đường thẳng \(d\) có phương trình: \(\frac{{x + 2}}{3} = \frac{{y - 5}}{{ - 5}} = \frac{{z - 2}}{{ - 1}}\) và mặt phẳng\(\left( P \right)\): \[2x + z - 2 = 0\]. Phương trình đường thẳng \[\Delta \] qua \[M\] vuông góc với \[d\] và song song với \[\left( P \right)\] là     

Trong không gian với hệ trục tọa độ \(Oxyz\), mặt phẳng \(\left( \alpha \right):3x - 2y - z + 5 = 0\) vuông góc với mặt phẳng nào dưới đây?     

Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(M\left( {1;2; - 3} \right),\,\,N\) và vectơ \(\vec v = \left( {2; - 1; - 2} \right)\) thỏa mãn điều kiện \(\vec v = \overrightarrow {MN} \). Tọa độ của điểm \(N\) là     

Trong không gian với hệ trục tọa độ \[Oxyz\], tìm tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 2y - 4z - 2 = 0\].     

Trong không gian với hệ trục tọa độ \[Oxyz\], cho điểm \[M\left( {2; - 1;4} \right)\]và mặt phẳng \[\left( P \right)\] có phương trình \[3x - 2y + z + 1 = 0\]. Phương trình của mặt phẳng đi qua M và song song với mặt phẳng \[\left( P \right)\]là     

PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một sân vận động được xây dựng theo mô hình là hình chóp cụt \(OAGD.BCFE\)có hai đáy song song với nhau. Mặt sân \(OAGD\) là hình chữ nhật và được gắn hệ trục \[Oxyz\]như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân \(OAGD\)có chiều dài \(OA = 100\,\,{\rm{m}}\), chiều rộng \(OD = 60\,\,{\rm{m}}\) và tọa độ điểm \(B\left( {10;10;8} \right)\).

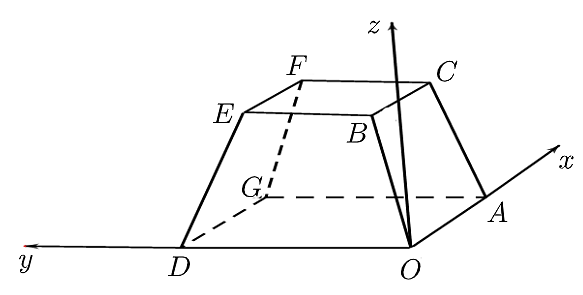
a)\(\overrightarrow {OD} = \left( {0;60;0} \right)\).

b)\(G\left( {100;\,\,0;\,\,60} \right)\).

c)Phương trình mặt phẳng \(\left( {OBED} \right)\) là: \(4x - 5z = 0\).

d)Khoảng cách từ điểm \(G\) đến mặt phẳng \(\left( {OBED} \right)\)(kết quả làm tròn đến chữ số thập phân thứ nhất) là \(62,4\,\,{\rm{m}}\).

Trong không gian với hệ trục tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\frac{x}{{ - 1}} = \frac{{y + 3}}{2} = \frac{{z - 2}}{3}\)và mặt phẳng \(\left( P \right):x + 2y - z + 2025 = 0\).

a) Số đo góc giữa đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\) bằng \(90^\circ \).

b)Biết hình chiếu của\(O\) lên mặt phẳng \(\left( \alpha \right)\) là\(H\left( {3; - 1;2} \right)\), \(\alpha \)là số đo góc giữa mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \), khi đó \({\rm{cos}}\alpha = \frac{1}{{14}}\).

c) Đường thẳng \({d_1}\) là giao tuyến của hai mặt phẳng \(\left( P \right)\)và \(\left( {Oxy} \right)\). Gọi \(\beta \) là góc giữa \({d_1}\) và mặt phẳng \[\left( {Oxz} \right)\]. Khi đó \(\beta > 30^\circ \).

d) Đường thẳng \({d_2}\)vuông góc với \(\left( P \right)\) tạo với \[\left( Q \right):x + my - 3 = 0\] một góc \(30^\circ \). Khi đó tổng tất cả các giá trị của tham số \(m\) bằng \(\frac{{ - 8}}{5}\).

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):{\left( {x + 2} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 36\) và điểm \(A\left( { - 4; - 1;4} \right)\).

a) Tọa độ tâm \(I\) của mặt cầu \(\left( S \right)\) là \(\left( {2; - 3;0} \right)\).

b) Mặt cầu \(\left( S \right)\) đi qua điểm \(A\).

c) Điểm \(B\left( {1;\,7;\,3} \right)\) nằm bên ngoài mặt cầu \(\left( S \right)\).

d) Mặt phẳng \(\left( P \right):2x - y + 2z - 11 = 0\) tiếp xúc mặt cầu \(\left( S \right)\).

Trong không gian với hệ trục tọa độ \[Oxyz\], cho hình lăng trụ \[ABC.A'B'C'\] có điểm \[A\] trùng với gốc tọa độ \[O\], các điểm \[B\left( {2;0;0} \right)\], \[C\left( {0;3;0} \right)\] và \[B'\left( {0;0;4} \right)\].

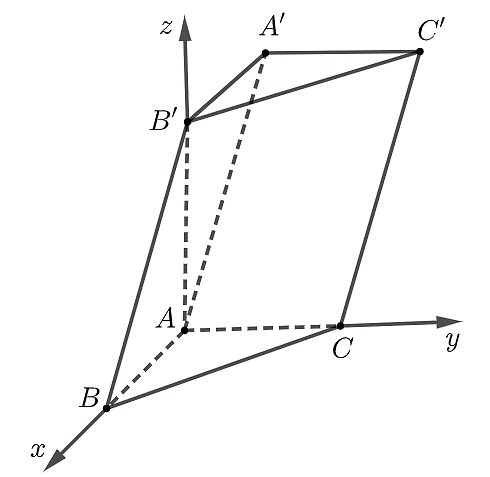
a)Thể tích của khối lăng trụ \[ABC.A'B'C'\] là \[V = 24\].

b) Nếu \[\overrightarrow u = \overrightarrow {A'B} + \overrightarrow {A'C} \] thì \[\overrightarrow u = \left( {6;3; - 8} \right)\].

c) Tọa độ của điểm \[C'\] là \[C'\left( { - 2;3;4} \right)\].

d) Chiếu hình lăng trụ đã cho lên mặt phẳng \[\left( {Oyz} \right)\], ta được một đa giác có diện tích bằng \[8\].

PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.

Trong không gian với hệ trục tọa độ \[Oxyz\], cho các điểm \[A\left( {1;0;0} \right)\], \[B\left( {0;b;0} \right)\], \[C\left( {0;0;c} \right)\] trong đó \[b,c\] là các số hữu tỷ dương và mặt phẳng \[\left( P \right)\] có phương trình \[y - z + 1 = 0\]. Biết rằng mặt phẳng \[\left( {ABC} \right)\]vuông góc với mặt phẳng \[\left( P \right)\] và khoảng cách từ \[O\] đến mặt phẳng \[\left( {ABC} \right)\] bằng \[\frac{1}{3}\]. Tính \[b + c\].

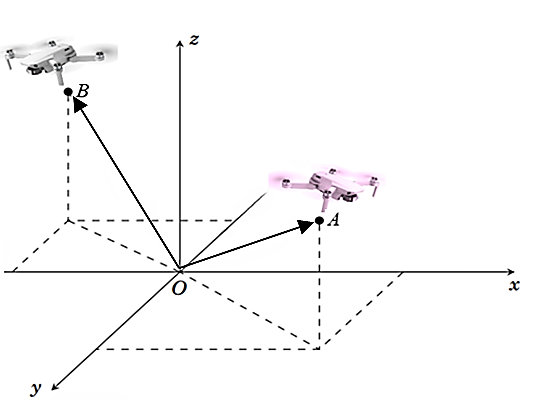
Trạm không lưu sân bay Đà Nẵng xây dựng hệ tọa độ \(Oxyz\) (gốc \(O\)đặt tại Đà Nẵng) để theo dõi vị trí các chuyến bay. Lúc \(6\) giờ máy bay \(A\) xuất phát từ Đà Nẵng đến TP. Hồ Chí Minh theo tia \(OA\)lần lượt hợp với ba tia \[Ox\], \(Oy\), \(Oz\) các góc bằng nhau với vận tốc \(800\)km/h. Mười phút sau máy bay \(B\) đi Hà Nội theo tia \(OB\) hợp với ba tia \(Ox'\), \(Oy'\), \(Oz\) các góc bằng nhau với vận tốc \(900\)km/h (hình vẽ minh họa). Tính khoảng cách (đơn vị kilômét và làm tròn đến hàng đơn vị) giữa hai máy bay \(A\) và \(B\) lúc \(6\) giờ \(30\) phút.

Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( { - 1\,;\,\,2\,;\,\,4} \right)\), \(B\left( { - 1\,;\,\, - 2\,;\,\,2} \right)\) và điểm \(M\left( {a\,;\,\,b\,;\,\,1} \right)\) sao cho tam giác \(MAB\) vuông tại \(M\) và diện tích tam giác \(MAB\) nhỏ nhất. Khi đó \({a^3} + {b^3}\) bằng bao nhiêu?

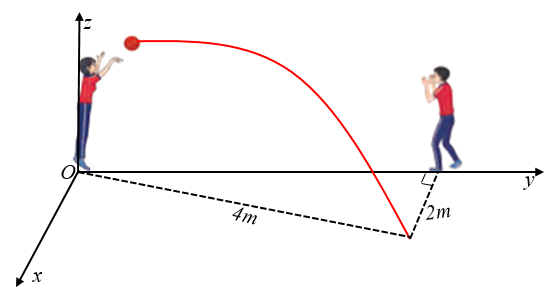
Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam \(2\,{\rm{m}}\), cách bạn nữ \(4\,{\rm{m}}\). Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( P \right)\) vuông góc với mặt đất. Biết rằng phương trình của \(\left( P \right)\) trong không gian \[Oxyz\] được mô tả như trong hình vẽ và có dạng \(\left( P \right):ax + by + cz = 0\). Khi đó giá trị của \({a^2} - {b^2} + {c^2}\) bằng bao nhiêu?

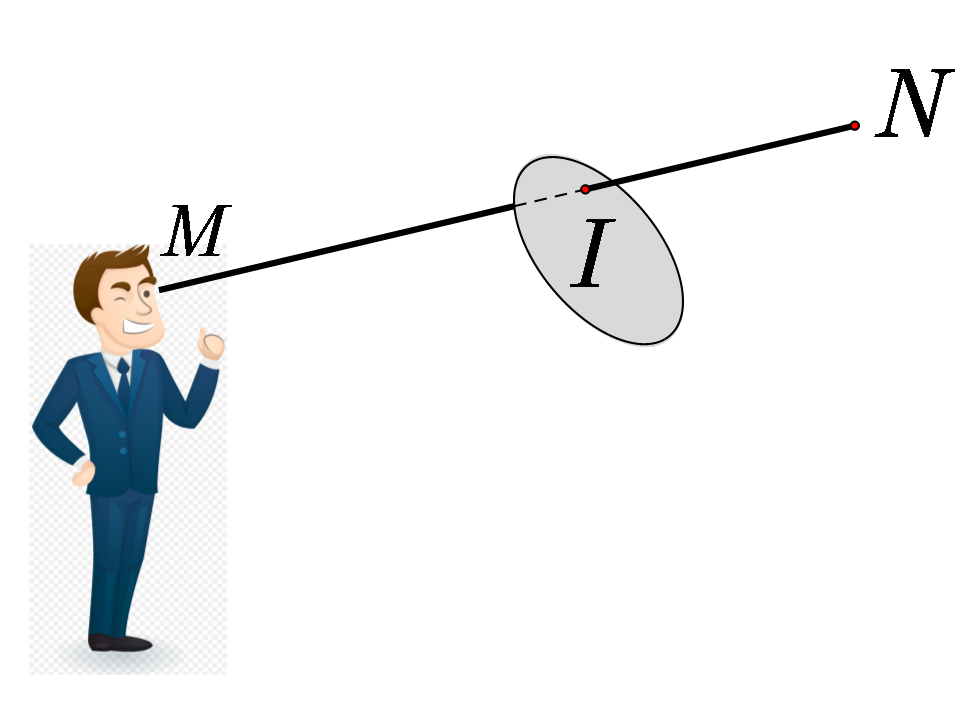
Trong không gian với hệ trục tọa độ \[Oxyz,\] mắt một người quan sát đặt tại điểm \[M\left( {1;2;3} \right)\] và vật cần quan sát đặt tại điểm \[N\left( {2;3; - 12} \right)\]. Một tấm bìa cứng có dạng hình tròn thuộc mặt phẳng \[\left( {Oxy} \right)\] tâm đặt tại gốc tọa độ, bán kính \[R\] che khuất tầm nhìn của người quan sát. Khi đó bán kính của tấm bìa nhỏ nhất là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Trong không gian với hệ trục tọa độ \(Oxyz\),có 3 diễn viên xiếc nhào lộn đang ở 3 vị trí \(A\left( {1\,; - 2\,;\,3} \right)\),\(B\left( {3\,;\,4\,;\,1} \right)\),\(C\left( { - 5\,;\,2\,;\,1} \right)\).Gọi\(\left( \alpha \right)\)là một mặtphẳng lưới bảo hộ di độngluôn  chứa trục hoành sao cho \(A\), \(B\), \(C\)nằm cùng phía với \(\left( \alpha \right)\)và \({d_1},\,{d_2},\,{d_3}\) lần lượt là khoảng cách từ \(A,\) \(B\), \(C\)đến \(\left( \alpha \right)\). Tiết mục xiếc sẽ được bắt đầu khi mặt phẳng \(\left( \alpha \right)\) được điều chỉnh để biểu thức \(T = {d_1} + 2{d_2} + 3{d_3}\) đạt giá trị lớn nhất. Biết \(T\)lớn nhất bằng \(a\sqrt b \)(với \(a \in \mathbb{N}\), \(b\)là số nguyên tố). Hãy tính giá trị của biểu thức \(S = 2{\rm{a}} + 3b\).