Đề ôn luyện Toán theo Chủ đề 6. Vectơ và phương pháp tọa độ trong không gian (Đề số 1)
22 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1\,; - 1\,;2} \right)\), \(B\left( {2\,;0\,;1} \right)\), \(C\left( {0\,; - 1\,;3} \right)\). Giá trị của \(\overrightarrow {AB} \cdot \overrightarrow {AC} \)bằng
\(0\).
\( - 4\).
\( - 2\).
\(20\).
Trong không gian với hệ tọa độ \[Oxyz\], đường thẳng \[d:\left\{ \begin{array}{l}x = 2t\\y = 1 - 4t\\z = 2 + t\end{array} \right.\;\,\left( {t \in \mathbb{R}} \right)\] nhận vectơ nào dưới đây làm vectơ chỉ phương?
\(\left( {2; - 4; - 1} \right)\).
\(\left( { - 2;4; - 1} \right)\).
\(\left( {2;4;1} \right)\).
\(\left( { - 2;4;1} \right)\).
Trong không gian với hệ toạ độ \[Oxyz\], khoảng cách từ điểm \[A\left( {3; - 2;4} \right)\] đến mặt phẳng \[\left( {Oxz} \right)\] bằng
4.
5.
3.
2.
Trong không gian với hệ tọa độ\[Oxyz\], cho mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 2z - 7 = 0\]. Bán kính của mặt cầu đã cho bằng
\[3\].
\[\sqrt {15} \].
\[\sqrt 7 \].
\[9\].
Trong không gian với hệ tọa độ \(Oxyz\), gọi \(M'\) là hình chiếu vuông góc của điểm \(M\left( {1;3; - 2} \right)\) trên trục \(Oz\). Khi đó vectơ \(\overrightarrow {MM'} \) có tọa độ là
\(\left( {1;3;0} \right)\).
\(\left( {0;0;2} \right)\).
\(\left( { - 1; - 3;0} \right)\).
\(\left( {0;0; - 2} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng\[d\] có phương trình tham số là \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - t\\z = - 3 + t\end{array} \right.\,\left( {t \in \mathbb{R}} \right)\). Khi đó phương trình chính tắc của đường thẳng \(d\) là
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z + 3}}{1}\).
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{1}\).
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{1} = \frac{{z + 3}}{1}\).
\(\frac{{x + 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{1}\).
Trong chương trình trại hè 2024 – 2025 một nhóm học sinh trường THPT X được giao làm 1 trại hè như hình vẽ. Để trang trí trại cần lắp 1 bóng đèn màu ở vị trí đỉnh trại \(O\). Đặt ổ điện nằm trên mặt đất, hỏi độ dài đoạn dây điện ngắn nhất từ ổ điện đến bóng đèn là bao nhiêu để tiết kiệm chi phí. Biết \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau.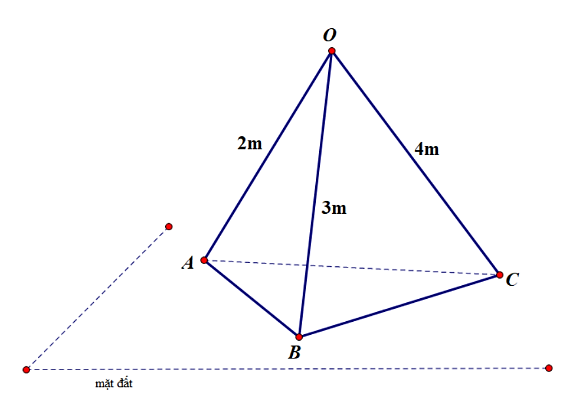
\(\frac{{9\sqrt {62} }}{{62}}\).
\(\frac{{12\sqrt {63} }}{{63}}\).
\(\frac{{12\sqrt {61} }}{{61}}\).
\(\frac{{6\sqrt {61} }}{{61}}\).
Trong không gian với hệ trục tọa độ \[Oxyz\], cho hai điểm \[A\left( {1\,; - 2\,;3} \right)\] và \[B\left( {3\,;1\,;1} \right)\]. Đường thẳng \[AB\] có phương trình là
\[\frac{{x - 1}}{4} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{4}\].
\[\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z - 3}}{{ - 2}}\].
\[\frac{{x - 4}}{1} = \frac{{y + 1}}{{ - 2}} = \frac{{z - 4}}{3}\].
\[\frac{{x - 2}}{2} = \frac{{y - 3}}{{ - 2}} = \frac{{z + 2}}{3}\].
Trong không gian với hệ trục tọa độ \[Oxyz\], cho điểm \(A\left( {2\,;\, - 3\,;\,1} \right)\). Gọi \(B\) là điểm đối xứng với \(A\) qua mặt phẳng \(\left( {Oxy} \right)\). Tọa độ của điểm \(B\) là
\(B\left( { - 2\,;\,3\,;\,1} \right)\).
\(B\left( {2\,;\, - 3\,;\, - 1} \right)\).
\(B\left( {2\,;\, - 3\,;\,0} \right)\).
\(B\left( { - 2\,;\,3\,;\,0} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho mặt phẳng \(\left( \alpha \right):x + 2y - z - 3 = 0\). Khi đó, góc giữa mặt phẳng \(\left( \alpha \right)\) và mặt phẳng \(\left( R \right):3x - 3y - 5z + 2 = 0\) gần nhất với giá trị nào sau đây?
\[52,2^\circ \].
\[97,2^\circ \].
\[82,8^\circ \].
\[62,8^\circ \].
Cho hình lập phương\[ABCD.A'B'C'D'\]. Gọi \[O\] là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
\[\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\] .
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\] .
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {4;\,1;\,0} \right)\) và \(B\left( {2;\, - 1;\,2} \right)\). Phương trình mặt phẳng trung trực của đoạn thẳng \(AB\)là
\(x + y - z - 4 = 0\).
\(3x + z - 4 = 0\).
\(3x + z - 2 = 0\).
\(x + y - z - 2 = 0\).
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tứ diện \(S.ABC\) có ba cạnh \(SA,{\rm{ }}SB,{\rm{ }}SC\) đôi một vuông góc với nhau và \(SA = 2,\)\(SB = 2,SC = 3\). Gọi điểm \(G\) là trọng tâm của tam giác \(ABC\).
a) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \).
b) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {GS} \).
c)Tích vô hướng của hai vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {CG} \) bằng \(\frac{4}{3}\).
d) Tang góc giữa hai vectơ \(\overrightarrow {BS} \)và \(\overrightarrow {GC} \) bằng \(\sqrt {10} \).
Cho hình minh hoạ sơ đồ một ngôi nhà trong hệ trục toạ độ\(Oxyz\), trong đó nền nhà, bốnbức tường và hai mái nhà đều là hình chữ nhật.
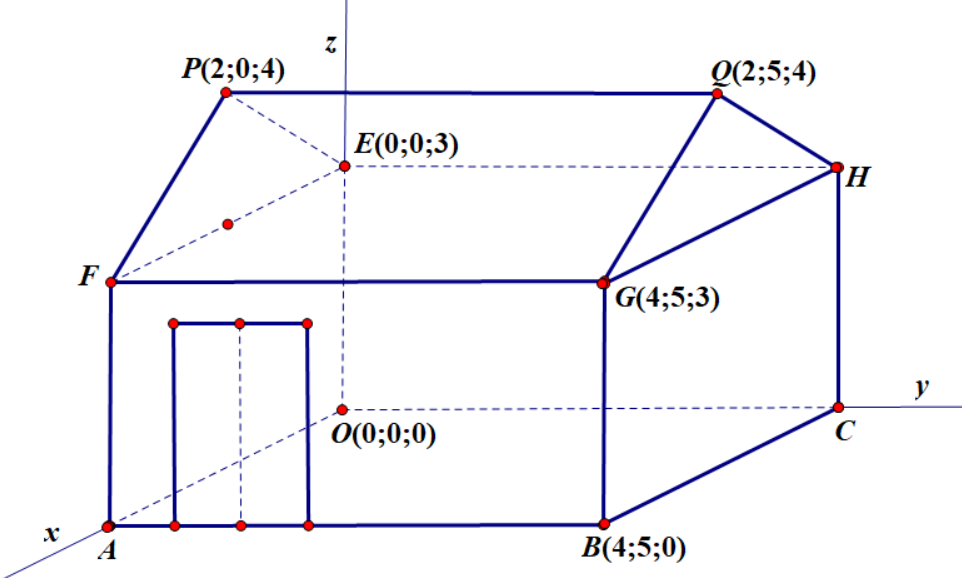
a) Toạ độ điểm \(A\) là \(\left( {4;0;0} \right)\).
b) Toạ độ điểm \(H\) là \(\left( {0;5;3} \right)\).
c) Góc dốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng \(FG\), hai mặt lần lượt là \(\left( {FGQP} \right)\) và \(\left( {FGHE} \right)\) xấp xỉ bằng \(26,6^\circ \).
d) Người ta cần nối một sợi dây điện từ điểm \(A\) đến mặt mái \(\left( {PQHE} \right)\). Độ dài tối thiểu của sợi dây điện nhỏ hơn \(4,4\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1;\,2;\,5} \right)\) và mặt phẳng\(\left( \alpha \right):x + 2y + 2z - 6 = 0\).
a) Vectơ \(\overrightarrow n = \left( {1;2;2} \right)\)là một vectơ pháp tuyến của \(\left( \alpha \right)\).
b) Mặt phẳng \(\left( \beta \right)\) đi qua điểm \(A\)và song song với mặt phẳng \(\left( \alpha \right)\)có phương trình là\(x + 2y + 2z + 15 = 0\).
c) Phương trình mặt phẳng \(\left( \gamma \right)\) đi qua hai điểm \(O\) và \(A\) đồng thời vuông góc với mặt phẳng \(\left( \alpha \right)\)là \(2x - y = 0\).
d) Điểm \(M\left( {a\,;\,b\,;\,c} \right) \in \left( \alpha \right)\)sao cho \(A,O,M\) thẳng hàng. Khi đó \(5a + 10b + c = 12\).
Trong không gian với hệ tọa độ \[Oxyz\], cho hai đường thẳng \({d_1}:\frac{{x - 3}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z - 1}}{3}\)và \({d_2}:\left\{ \begin{array}{l}x = - 2t\\y = 1 + t\\z = 2 - 3t\end{array} \right.\;\left( {t \in \mathbb{R}} \right)\).
a) Điểm \(M\left( { - 2;2; - 1} \right)\) nằm trên đường thẳng \({d_2}\).
b) Hai đường thẳng \({d_1}\)và \({d_2}\)vuông góc với nhau.
c)Côsin của góc giữa hai đường thẳng \({d_1}\)và \({d_2}\) bằng \( - \frac{5}{{14}}\).
d)Hai đường thẳng \({d_1}\)và \({d_2}\)cắt nhau.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Trong không gian cho bốn điểm \(A,B,C,D\) thỏa mãn \(\overrightarrow {OA} = \frac{1}{2}\overrightarrow {OB} + \frac{1}{3}\overrightarrow {OC} + x\overrightarrow {OD} \) với \(O\) là một điểm bất kì. Ta xác định được \(x\) để bốn điểm \(A,B,C,D\) đồng phẳng là \(x = \frac{m}{n}\) với \(\frac{m}{n}\) là phân số tối giản, khi đó \(n - m\) bằng bao nhiêu?
Trong không gian với hệ tọa độ \(Oxyz,\)cho ba điểm \[A\left( {1;1;1} \right)\], \[B\left( { - 2;1;0} \right)\] và \[C\left( {2; - 3;1} \right)\]. Điểm \(S\left( {a;b;c} \right) \in \left( {Oyz} \right)\) sao cho \(P = S{A^2} + S{B^2} + 3S{C^2}\) đạt giá trị nhỏ nhất. Tính giá trị của biểu thức \(T = a - 5b + 5c\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai điểm \(A\left( { - 1;\;2;\;0} \right),\;B\left( {1;\;1;\;3} \right)\) và mặt phẳng \(\left( P \right):x - 2y + 3z - 5 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua hai điểm \(A,\;B\) và vuông góc \(\left( P \right)\) có phương trình là \(2x - ay - bz + c = 0.\) Tính giá trị của biểu thức \(a + 2b + 3c\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;0; - 2} \right),\,\,B\left( {3;2;2} \right)\). Tập hợp điểm \(M\left( {x;y;z} \right)\) thay đổi thỏa mãn \(\overrightarrow {MA} \cdot \overrightarrow {MB} = 10\) nằm trên mặt cầu bán kính \(R\). Tìm bán kính \(R\).
Trong không gian \(Oxyz\), cho điểm \(A\left( {1\,; - 1\,;\,2} \right)\), đường thẳng \(d:\,\frac{{x + 1}}{2} = \frac{y}{1} = \frac{{z - 2}}{1}\) và mặt phẳng \(\left( P \right):x + y - 2{\rm{z}} + 5 = 0\). Xét đường thẳng \(\Delta \) cắt \(d\) và \(\left( P \right)\) tại lần lượt hai điểm \(M,{\rm{ }}N\) sao cho \(A\) là trung điểm của đoạn thẳng\(MN\). Biết vectơ \(\overrightarrow u \, = \left( {1\,;\,a\,;\,b} \right)\)là một vectơ chỉ phương của đường thẳng \(\Delta \). Tính giá trị của biểu thức \(4a + b\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hình lập phương \(OBCD.O'B'C'D'\) có cạnh bằng \(9\) sao cho điểm \(D\) thuộc tia \[Ox\], điểm \(B\) thuộc tia \(Oy\) và điểm \(O'\) thuộc tia \(Oz\). Điểm \(M\) thuộc cạnh \(O'B'\) sao cho \(O'B' = 3O'M\). Một con kiến bò từ vị trí \(M\) qua sáu mặt của hình lập phương đã cho rồi quay lại vị trí điểm \(M\) sao cho quãng đường đi được của con kiến là ngắn nhất. Hỏi với cách bò như vậy, con kiến đã bò qua bao nhiêu điểm mà điểm đó có hoành độ, tung độ và cao độ là các số nguyên dương?

