12 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1\,; - 1\,;2} \right)\), \(B\left( {2\,;0\,;1} \right)\), \(C\left( {0\,; - 1\,;3} \right)\). Giá trị của \(\overrightarrow {AB} \cdot \overrightarrow {AC} \)bằng
\(0\).
\( - 4\).
\( - 2\).
\(20\).
Trong không gian với hệ tọa độ \[Oxyz\], đường thẳng \[d:\left\{ \begin{array}{l}x = 2t\\y = 1 - 4t\\z = 2 + t\end{array} \right.\;\,\left( {t \in \mathbb{R}} \right)\] nhận vectơ nào dưới đây làm vectơ chỉ phương?
\(\left( {2; - 4; - 1} \right)\).
\(\left( { - 2;4; - 1} \right)\).
\(\left( {2;4;1} \right)\).
\(\left( { - 2;4;1} \right)\).
Trong không gian với hệ toạ độ \[Oxyz\], khoảng cách từ điểm \[A\left( {3; - 2;4} \right)\] đến mặt phẳng \[\left( {Oxz} \right)\] bằng
4.
5.
3.
2.
Trong không gian với hệ tọa độ\[Oxyz\], cho mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 2z - 7 = 0\]. Bán kính của mặt cầu đã cho bằng
\[3\].
\[\sqrt {15} \].
\[\sqrt 7 \].
\[9\].
Trong không gian với hệ tọa độ \(Oxyz\), gọi \(M'\) là hình chiếu vuông góc của điểm \(M\left( {1;3; - 2} \right)\) trên trục \(Oz\). Khi đó vectơ \(\overrightarrow {MM'} \) có tọa độ là
\(\left( {1;3;0} \right)\).
\(\left( {0;0;2} \right)\).
\(\left( { - 1; - 3;0} \right)\).
\(\left( {0;0; - 2} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng\[d\] có phương trình tham số là \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - t\\z = - 3 + t\end{array} \right.\,\left( {t \in \mathbb{R}} \right)\). Khi đó phương trình chính tắc của đường thẳng \(d\) là
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z + 3}}{1}\).
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{1}\).
\(\frac{{x - 1}}{2} = \frac{{y - 2}}{1} = \frac{{z + 3}}{1}\).
\(\frac{{x + 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{1}\).
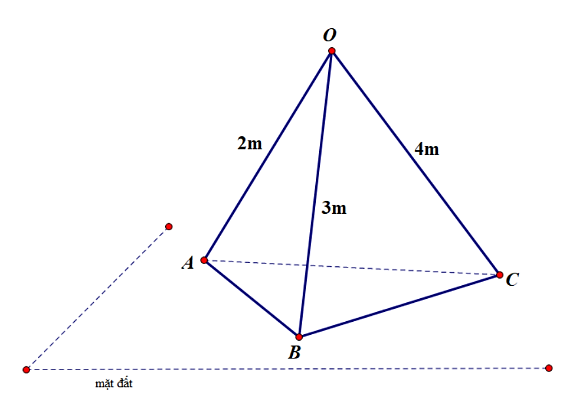
Trong chương trình trại hè 2024 – 2025 một nhóm học sinh trường THPT X được giao làm 1 trại hè như hình vẽ. Để trang trí trại cần lắp 1 bóng đèn màu ở vị trí đỉnh trại \(O\). Đặt ổ điện nằm trên mặt đất, hỏi độ dài đoạn dây điện ngắn nhất từ ổ điện đến bóng đèn là bao nhiêu để tiết kiệm chi phí. Biết \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau.
\(\frac{{9\sqrt {62} }}{{62}}\).
\(\frac{{12\sqrt {63} }}{{63}}\).
\(\frac{{12\sqrt {61} }}{{61}}\).
\(\frac{{6\sqrt {61} }}{{61}}\).
Trong không gian với hệ trục tọa độ \[Oxyz\], cho hai điểm \[A\left( {1\,; - 2\,;3} \right)\] và \[B\left( {3\,;1\,;1} \right)\]. Đường thẳng \[AB\] có phương trình là
\[\frac{{x - 1}}{4} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{4}\].
\[\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z - 3}}{{ - 2}}\].
\[\frac{{x - 4}}{1} = \frac{{y + 1}}{{ - 2}} = \frac{{z - 4}}{3}\].
\[\frac{{x - 2}}{2} = \frac{{y - 3}}{{ - 2}} = \frac{{z + 2}}{3}\].
Trong không gian với hệ trục tọa độ \[Oxyz\], cho điểm \(A\left( {2\,;\, - 3\,;\,1} \right)\). Gọi \(B\) là điểm đối xứng với \(A\) qua mặt phẳng \(\left( {Oxy} \right)\). Tọa độ của điểm \(B\) là
\(B\left( { - 2\,;\,3\,;\,1} \right)\).
\(B\left( {2\,;\, - 3\,;\, - 1} \right)\).
\(B\left( {2\,;\, - 3\,;\,0} \right)\).
\(B\left( { - 2\,;\,3\,;\,0} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho mặt phẳng \(\left( \alpha \right):x + 2y - z - 3 = 0\). Khi đó, góc giữa mặt phẳng \(\left( \alpha \right)\) và mặt phẳng \(\left( R \right):3x - 3y - 5z + 2 = 0\) gần nhất với giá trị nào sau đây?
\[52,2^\circ \].
\[97,2^\circ \].
\[82,8^\circ \].
\[62,8^\circ \].
Cho hình lập phương\[ABCD.A'B'C'D'\]. Gọi \[O\] là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
\[\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\] .
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\] .
Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {4;\,1;\,0} \right)\) và \(B\left( {2;\, - 1;\,2} \right)\). Phương trình mặt phẳng trung trực của đoạn thẳng \(AB\)là
\(x + y - z - 4 = 0\).
\(3x + z - 4 = 0\).
\(3x + z - 2 = 0\).
\(x + y - z - 2 = 0\).
