Đề ôn luyện Toán theo Chủ đề 5. Hình học không gian (Đề số 2)
22 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a\), \(BC = 2a\) và \(AA' = 3a\).Khoảng cách giữa hai đường thẳng \(BD\) và \(A'C'\) bằng
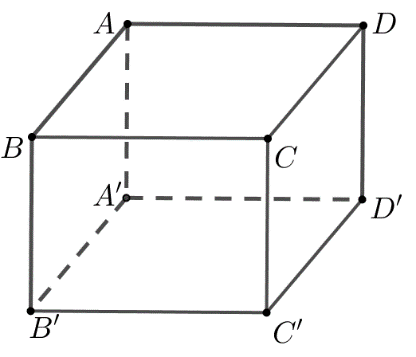
\(a\).
\(\sqrt 2 a\).
\(2a\).
\(3a\).
Cho tứ diện đều \(ABCD\). Gọi \(\varphi \) là góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\). Tính \({\rm{cos}}\varphi \).
\({\rm{cos}}\varphi = 0\).
\({\rm{cos}}\varphi = \frac{{\sqrt 3 }}{3}\).
\({\rm{cos}}\varphi = \frac{1}{2}\).
\({\rm{cos}}\varphi = \frac{{\sqrt 2 }}{3}\).
Một tấm bìa hình vuông có cạnh 50 cm. Người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh 16 cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Thể tích khối hộp chữ nhật vừa tạo thành là
5184 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
8704 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
4608 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
18496 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(5a\).
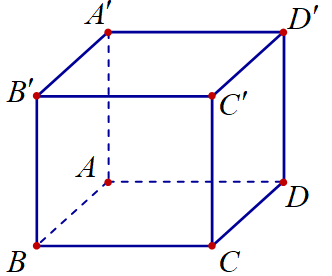
Khoảng cách giữa hai đường thẳng \(A'B'\) và \(AD\) bằng
\(2a\).
\(5a\).
\(3a\).
\(\sqrt 3 a\).
Cho hình chóp \[S.ABCD\] có tất cả các cạnh đều bằng nhau. Gọi \[I\] và \[J\] lần lượt là trung điểm của \[SC\] và \[BC\]. Số đo của góc \[\left( {IJ,CD} \right)\] bằng
\(90^\circ \).
\(45^\circ \).
\(60^\circ \).
\(30^\circ \).
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu \(2{\rm{\;m}}\). Cho biết \(AB = 1\;\,{\rm{m;}}\,\,AD = 3,5\;\,{\rm{m}}\). Tính tan của góc giữa đường thẳng \(BD\) và đáy hố (làm tròn kết quả đến hàng phần trăm).
\(2,54\).
\(0,66\).
\(0,52\).
\(1,02\).
Cho hình chóp \[S.ABCD\] có đáy là hình chữ nhật và \[SA\] vuông góc với mặt đáy. Góc nào dưới đây là góc giữa hai mặt phẳng \[\left( {SCD} \right)\] và \[\left( {ABCD} \right)\]? 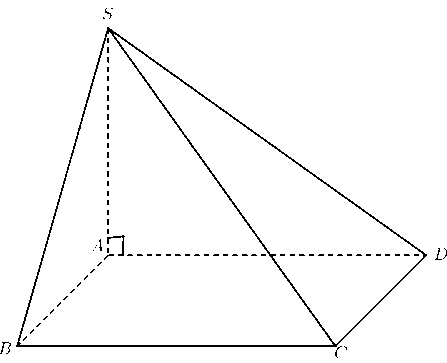
\[\widehat {SAD}\].
\[\widehat {SDA}\].
\[\widehat {SDC}\].
\[\widehat {ASC}\].
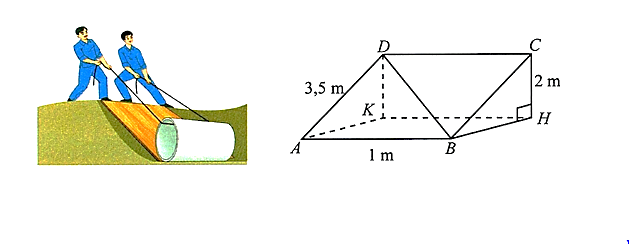
Một khúc gỗ có dạng và độ dài các cạnh được cho như hình vẽ. Thể tích khúc gỗ là 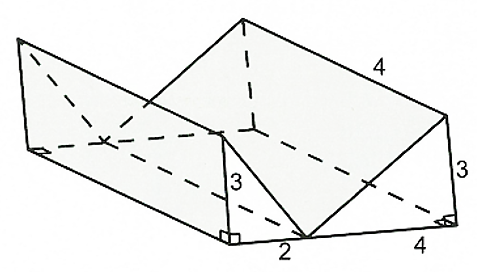
\(V = 12\).
\(V = 36\).
\(V = 96\).
\(V = 24\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = BC = a,\)\(AA' = \sqrt 6 a\). Góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABCD} \right)\) có số đo bằng 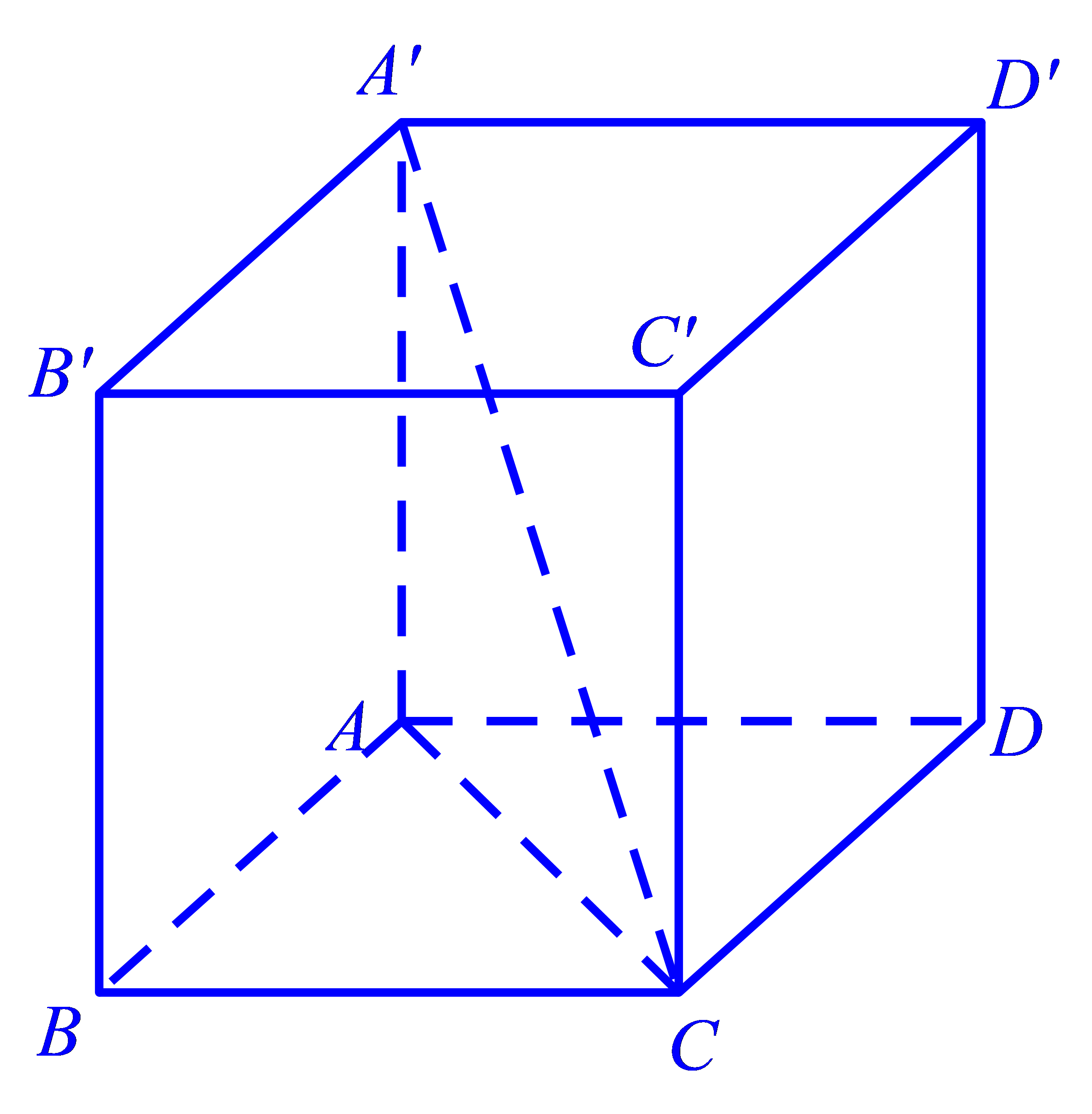
\(60^\circ \).
\(90^\circ \).
\(30^\circ \).
\(45^\circ \).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\), \(AB = a\), \(AC = a\sqrt 3 \), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 2a\). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
\[\frac{{2a\sqrt {57} }}{{17}}\].
\[\frac{{2a\sqrt {57} }}{{19}}\].
\[\frac{{2a\sqrt {57} }}{{21}}\].
\[\frac{{2a\sqrt {57} }}{{23}}\].
Cho hình chóp \[S.ABC\], đáy ABC có \[AB = 10{\rm{ cm}}\], \[BC = 12{\rm{ cm}}\], \[AC = 14{\rm{ cm}}\], các mặt bên cùng tạo với mặt phẳng đáy các góc bằng nhau và đều bằng \[\alpha \] thỏa mãn \[\tan \alpha = 3\]. Thể tích khối chóp \[S.ABC\] là
\[228{\rm{ c}}{{\rm{m}}^3}\].
\[576{\rm{ c}}{{\rm{m}}^3}\].
\[192{\rm{ c}}{{\rm{m}}^3}\].
\[384{\rm{ c}}{{\rm{m}}^3}\].
Cho lăng trụ \(ABCD.A'B'C'D'\) đáy là hình thang cân ABCD có \(AC \bot BD,AC = 2a\), cạnh \(AA'\) tạo với mặt phẳng đáy góc \(60^\circ \). Hình chiếu vuông góc của \(A'\) trên mặt phẳng \(\left( {ABCD} \right)\) là điểm H thuộc đoạn AC sao cho \(AH = \frac{1}{3}HC\). Thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) là
\(\frac{{2{a^3}\sqrt 3 }}{3}\).
\(2{a^3}\sqrt 3 \).
\(\frac{{{a^3}\sqrt 3 }}{3}\).
\({a^3}\sqrt 3 \).
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình chóp tam giác \(S.ABC\) có đáy là tam giác đều cạnh \(2a\), \(SA \bot \left( {ABC} \right)\)và \(SA = a\sqrt 3 \). Gọi \(M\)là trung điểm cạnh \(BC\).
a) \(SA \bot BC\).
b) Độ dài trung tuyến \[AM = a\].
c) \(BC \bot \left( {SAM} \right)\).
d)Số đo góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABC} \right)\] bằng \[60^\circ \].
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình thoi cạnh \(a\), \(\widehat {ABC} = 60^\circ \). Mặt bên \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(H,\,\,M,\,\,N\) lần lượt là trung điểm \(AB,\,\,SA\) và \(CD\).
a) \(SH \bot \left( {ABCD} \right)\).
b) Thể tích khối chóp \(S.ABCD\) bằng \(\frac{{{a^3}\sqrt 3 }}{4}\).
c) Gọi \(\alpha \) là số đo góc nhị diện \(\left[ {A,SC,B} \right]\). Khi đó \(\cos \alpha = - \frac{1}{5}\).
d) Khoảng cách giữa hai đường thẳng \(BM\) và \(SN\) bằng \(\frac{{a\sqrt {21} }}{{14}}\).
Cho hình chóp \(S.ABC\) có mặt bên \(\left( {SAB} \right)\) vuông góc với mặt đáy và tam giác \(SAB\) đều cạnh \(2a\) và điểm \(H\) là trung điểm \(AB\). Biết tam giác \(ABC\) vuông tại \(C\) và cạnh \(AC = a\sqrt 3 \).
a) \(SH \bot \left( {ABC} \right)\).
b)\(d\left( {S,\left( {ABC} \right)} \right) = a\sqrt 3 \).
c)\(d\left( {C,\left( {SAB} \right)} \right) = \frac{{a\sqrt 3 }}{3}\).
d) \[d\left( {B,\left( {SAC} \right)} \right) = \frac{{2a\sqrt 5 }}{{13}}\].
Ông An xây một bể bơi, ban đầu có dạng là hình hộp chữ nhật \(ABCD.A'B'C'D'\). Sau đó ông làm lại mặt đáy như hình vẽ.
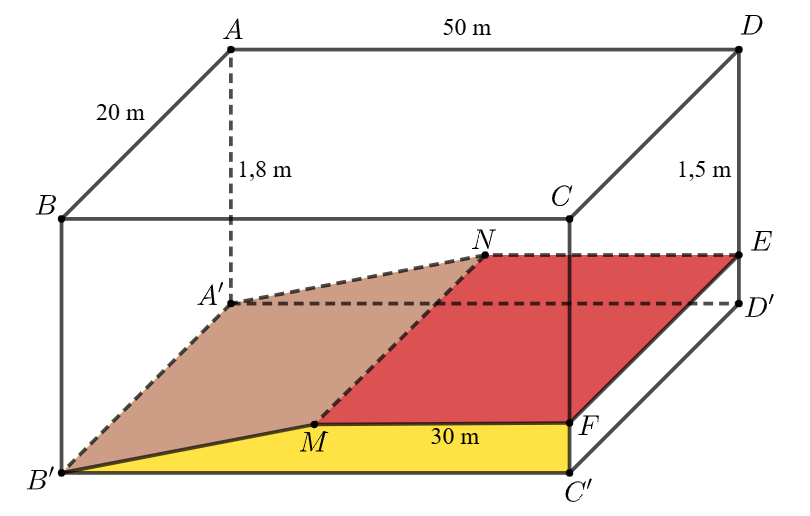
Biết rằng \(A'B'MN\) và \(MNEF\) là các hình chữ nhật, \(\left( {MNEF} \right){\rm{//}}\left( {A'B'C'D'} \right)\), \(AB = 20\,{\rm{m}}\), \(AD = 50\,{\rm{m}}\), \(AA' = 1,8\,{\rm{m}}\), \(MF = 30\,{\rm{m}}\), \(DE = 1,5\,{\rm{m}}\).
a) Cạnh BC của thành bể vuông góc với đường thẳng chứa MN của đáy bể.
b) Góc giữa thành bể \[ABB'A'\] và mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] gần bằng \(65^\circ 45'\).
c) Khoảng cách từ điểm B của góc bể đến mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] xấp xỉ bằng \(1,6599\,\,{\rm{m}}\).
d) Ông An bơm nước vào bể để phục vụ cho việc kinh doanh, đến khi mặt nước cách mép trên của thành bể \(0,2\,{\rm{m}}\) thì ông dừng lại, và giá tiền nước là 15 000 đồng/m3. Khi đó số tiền nước mà ông An phải trả là 20 400 000 đồng.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là \(100\% \), tương ứng với góc \(90^\circ \) (độ dốc \(10\% \) tương ứng với góc \(9^\circ \)). Giả sử có hai điểm \(A\), \(B\) nằm ở độ cao lần lượt là \(200\,\,{\rm{m}}\) và \(220\,\,{\rm{m}}\) so với mực nước biển và đoạn dốc \(AB\) dài \(120\,\,{\rm{m}}\). Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười)?
Cho hình chóp \[S.ABCD\] có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(I\) là điểm thuộc \(SO\) sao cho \(SI = \frac{1}{3}SO\). Mặt phẳng \(\left( \alpha \right)\) thay đổi đi qua \(B\) và \(I\) cắt các cạnh \(SA,\,SC,\,SD\) lần lượt tại \(M,\,N,\,P\). Gọi \(m,\,n\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của tỉ số \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}}\). Tính giá trị của biểu thức \(25m + 15n\).
Cho hình chóp \[S.ABCD\] có đáy là hình thang, \[AB = 2\], \[AD = DC = CB = 1\], \[SA\] vuông góc với mặt phẳng đáy và \[SA = 3\]. Gọi \[M\] là trung điểm của \[AB\]. Tính khoảng cách giữa hai đường thẳng \[SB\] và \[DM\] (viết kết quả dưới dạng số thập phân).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \(a\), cạnh bên \[SA\] vuông góc với mặt phẳng đáy. Gọi \[M\] là trung điểm của \[CD\]. Biết khoảng cách giữa hai đường thẳng \[BC\]và \[SM\] bằng \[\frac{{a\sqrt 3 }}{6}\]. Thể tích của khối chóp \[S.ABC\] được viết dưới dạng \[\frac{{{a^3}\sqrt m }}{n}\], với \[m\] là số nguyên tố. Khi đó, \[m - n\] bằng bao nhiêu?
Cho hình chóp \(S.ABCD\)có đáy là hình chữ nhật với \(AD = 2AB = 2a\). Biết hai mặt phẳng \(\left( {SAB} \right),\)\(\left( {SAD} \right)\)cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\)và \(SA = \frac{{a\sqrt {15} }}{{15}}\). Số đo góc giữa đường thẳng \(SB\)và mặt phẳng \(\left( {SAC} \right)\) bằng bao nhiêu độ?
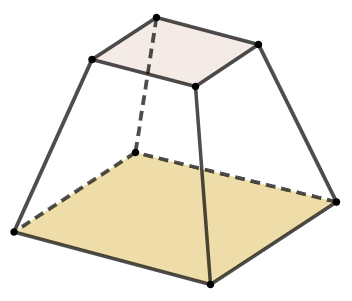
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều như hình vẽ. Cạnh đáy dưới dài \(5{\rm{\;m}}\), cạnh đáy trên dài \(2{\rm{\;m}}\), cạnh bên dài \(3{\rm{\;m}}\). Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng\(/{{\rm{m}}^3}\). Số tiền để mua bê tông tươi làm chân tháp hết bao nhiêu triệu đồng (làm tròn kết quả đến hàng đơn vị)?