12 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a\), \(BC = 2a\) và \(AA' = 3a\).Khoảng cách giữa hai đường thẳng \(BD\) và \(A'C'\) bằng
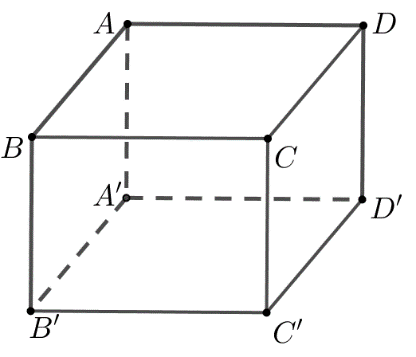
\(a\).
\(\sqrt 2 a\).
\(2a\).
\(3a\).
Cho tứ diện đều \(ABCD\). Gọi \(\varphi \) là góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\). Tính \({\rm{cos}}\varphi \).
\({\rm{cos}}\varphi = 0\).
\({\rm{cos}}\varphi = \frac{{\sqrt 3 }}{3}\).
\({\rm{cos}}\varphi = \frac{1}{2}\).
\({\rm{cos}}\varphi = \frac{{\sqrt 2 }}{3}\).
Một tấm bìa hình vuông có cạnh 50 cm. Người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh 16 cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Thể tích khối hộp chữ nhật vừa tạo thành là
5184 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
8704 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
4608 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
18496 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(5a\).
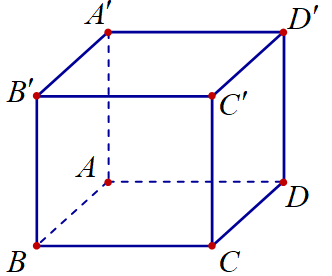
Khoảng cách giữa hai đường thẳng \(A'B'\) và \(AD\) bằng
\(2a\).
\(5a\).
\(3a\).
\(\sqrt 3 a\).
Cho hình chóp \[S.ABCD\] có tất cả các cạnh đều bằng nhau. Gọi \[I\] và \[J\] lần lượt là trung điểm của \[SC\] và \[BC\]. Số đo của góc \[\left( {IJ,CD} \right)\] bằng
\(90^\circ \).
\(45^\circ \).
\(60^\circ \).
\(30^\circ \).
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu \(2{\rm{\;m}}\). Cho biết \(AB = 1\;\,{\rm{m;}}\,\,AD = 3,5\;\,{\rm{m}}\). Tính tan của góc giữa đường thẳng \(BD\) và đáy hố (làm tròn kết quả đến hàng phần trăm).
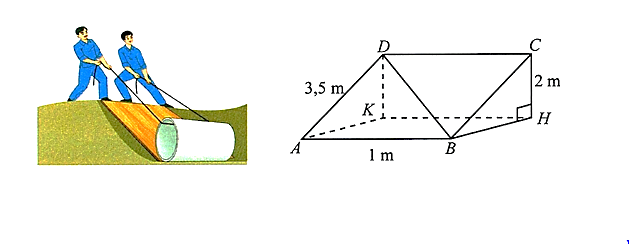
\(2,54\).
\(0,66\).
\(0,52\).
\(1,02\).
Cho hình chóp \[S.ABCD\] có đáy là hình chữ nhật và \[SA\] vuông góc với mặt đáy. Góc nào dưới đây là góc giữa hai mặt phẳng \[\left( {SCD} \right)\] và \[\left( {ABCD} \right)\]?
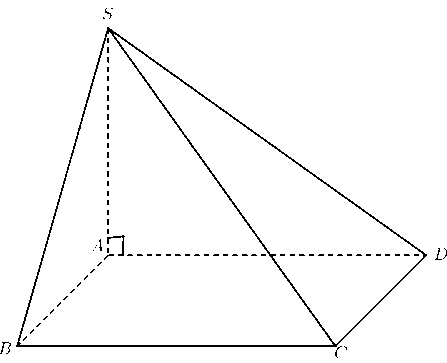
\[\widehat {SAD}\].
\[\widehat {SDA}\].
\[\widehat {SDC}\].
\[\widehat {ASC}\].
Một khúc gỗ có dạng và độ dài các cạnh được cho như hình vẽ. Thể tích khúc gỗ là
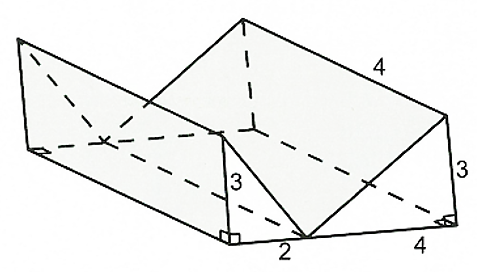
\(V = 12\).
\(V = 36\).
\(V = 96\).
\(V = 24\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = BC = a,\)\(AA' = \sqrt 6 a\). Góc giữa đường thẳng \(A'C\) và mặt phẳng \(\left( {ABCD} \right)\) có số đo bằng
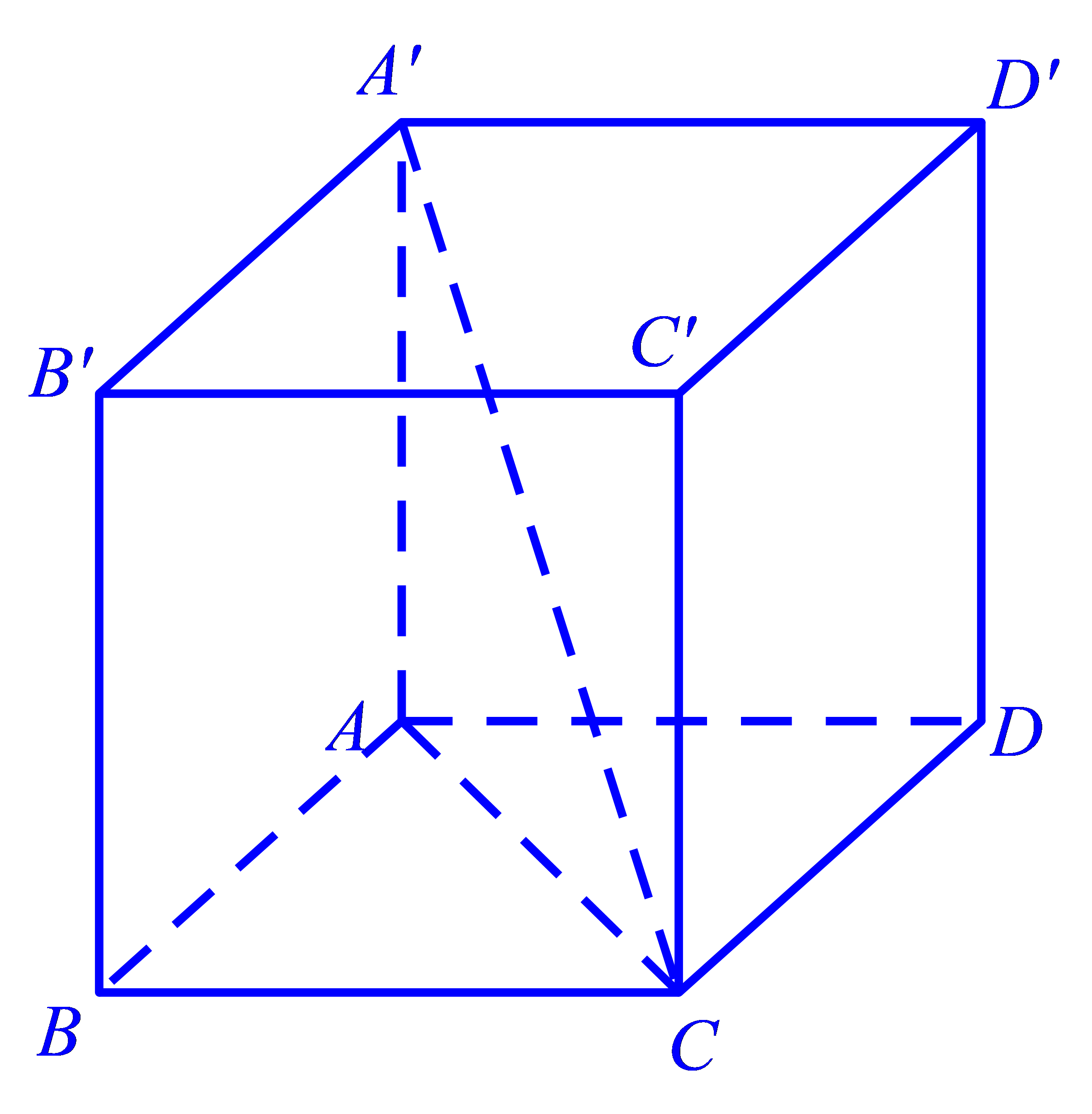
\(60^\circ \).
\(90^\circ \).
\(30^\circ \).
\(45^\circ \).
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\), \(AB = a\), \(AC = a\sqrt 3 \), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 2a\). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
\[\frac{{2a\sqrt {57} }}{{17}}\].
\[\frac{{2a\sqrt {57} }}{{19}}\].
\[\frac{{2a\sqrt {57} }}{{21}}\].
\[\frac{{2a\sqrt {57} }}{{23}}\].
Cho hình chóp \[S.ABC\], đáy ABC có \[AB = 10{\rm{ cm}}\], \[BC = 12{\rm{ cm}}\], \[AC = 14{\rm{ cm}}\], các mặt bên cùng tạo với mặt phẳng đáy các góc bằng nhau và đều bằng \[\alpha \] thỏa mãn \[\tan \alpha = 3\]. Thể tích khối chóp \[S.ABC\] là
\[228{\rm{ c}}{{\rm{m}}^3}\].
\[576{\rm{ c}}{{\rm{m}}^3}\].
\[192{\rm{ c}}{{\rm{m}}^3}\].
\[384{\rm{ c}}{{\rm{m}}^3}\].
Cho lăng trụ \(ABCD.A'B'C'D'\) đáy là hình thang cân ABCD có \(AC \bot BD,AC = 2a\), cạnh \(AA'\) tạo với mặt phẳng đáy góc \(60^\circ \). Hình chiếu vuông góc của \(A'\) trên mặt phẳng \(\left( {ABCD} \right)\) là điểm H thuộc đoạn AC sao cho \(AH = \frac{1}{3}HC\). Thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) là
\(\frac{{2{a^3}\sqrt 3 }}{3}\).
\(2{a^3}\sqrt 3 \).
\(\frac{{{a^3}\sqrt 3 }}{3}\).
\({a^3}\sqrt 3 \).
