Đề ôn luyện Toán theo Chủ đề 4. Nguyên hàm, tích phân và ứng dụng (Đề số 2)

Cho hàm số \(f\left( x \right) = - 1 + 2x + 3{x^2}\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và trục hoành có giá trị bằng     

Cho \(I = \int\limits_0^2 {f\left( x \right){\rm{d}}x = \,} 3\). Khi đó \(J = \int\limits_0^2 {\left[ {4f\left( x \right) - 3} \right]{\rm{d}}x} \) bằng     

Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ {a;c} \right]\) và \(b\) là số thực tùy ý thuộc đoạn \(\left[ {a;c} \right]\). Nếu biết \(\int\limits_a^b {f\left( x \right)} \,{\rm{d}}x = - 5\) và \(\int\limits_b^c {f\left( x \right)} \,{\rm{d}}x = 10\), thì giá trị của \(\int\limits_a^c {f\left( x \right)} \,{\rm{d}}x\) là      

Tìm nguyên hàm của hàm số \(f\left( x \right) = 2026\sin x\).     

Cho $\underset{0}{\overset{2}{\int }}\left[f\left(x\right)-3x^2\right]\text{d}x=4$. Tích phân \(\int\limits_0^2 {f\left( x \right){\rm{d}}x} \) bằng     

Họ nguyên hàm của hàm số \(f\left( x \right) = {3^{x - 1}} \cdot {5^{x + 1}}\) là     

Biết rằng \[\int\limits_2^3 {\frac{{3x + 1}}{{2{x^2} - x - 1}}{\rm{d}}x} = a\ln 2 + b\ln 5 + c\ln 7\] trong đó \[a,b,c \in \mathbb{Q}\]. Giá trị của biểu thức \[P = a + b + c\] là     

Cho \[y = F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right) = - 3{x^2} + 4x + 2\] và \[F\left( 1 \right) = 2\] . Tính \[F\left( { - 1} \right)\].     

Cho \[\int {\frac{1}{{x{{\ln }^2}x}}} \,{\rm{d}}x = F\left( x \right) + C\]. Khẳng định nào dưới đây đúng?     

Diện tích phần gạch sọc trong hình vẽ bên bằng   

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\) thoả mãn \(F\left( 5 \right) = 2 + F\left( 1 \right)\). Giá trị của \(\int\limits_1^5 {f\left( x \right){\rm{d}}x} \) bằng     

PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hàm số \(f\left( x \right) = \frac{x}{2} + \cos x\).

a) Hàm số \(f\left( x \right)\) có tập xác định là đoạn \[\left[ { - 1\,;\,1} \right]\].

b) \(\int {f\left( x \right){\rm{d}}x = {x^2} + \sin x} \).

c) \(\int\limits_0^2 {f\left( x \right){\rm{d}}x = 1 + \sin 2} \).

d) Nếu hàm số \(F\left( x \right)\)là một nguyên hàm của hàm số \(f\left( x \right)\)và thoả mãn \(F\left( 0 \right) = 1\) thì \(F\left( 1 \right) = \frac{1}{4}\).

Cho hàm số \[f\left( x \right) = \frac{{{x^2} + 5x - 7}}{x}\].

a) \[\int {f\left( x \right)} \,{\rm{d}}x = \frac{{{x^2}}}{2} + 5x - 7\ln x + C\].

b) Hàm số \[f\left( x \right)\] là một nguyên hàm của hàm số \[g\left( x \right) = \frac{{{x^2} + 7}}{{{x^2}}}\].

c) \[\int\limits_{ - 2}^{ - 1} {f\left( x \right){\rm{d}}} x = \frac{m}{n} + m\ln n\], với \[m,n \in {\mathbb{N}^ * }\], \[\frac{m}{n}\] là phân số tối giản. Tổng \[m + 2025n = 4057\].

d) Gọi \[G\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right)\] thỏa mãn \[G\left( 1 \right) = 4\] và \[G\left( 3 \right) + G\left( { - 9} \right) = 20\]. Khi đó \[G\left( { - 6} \right) = a\ln 2 + b\ln 3 + c\], với \[a,b,c\] là các số hữu tỉ. Tổng \[a + b + c = \frac{2}{3}\].

Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức \(P'\left( x \right) = - 0,0008x + 10,4\). Ở đây \(P\left( x \right)\) là lợi nhuận (tính bằng triệu đồng) khi bán được \(x\) đơn vị sản phẩm.

a) Lợi nhuận khi bán được \(x\) đơn vị sản phẩm được tính bằng công thức

\(P\left( x \right) = - 0,0008{x^2} + 10,4x\).

b) Lợi nhuận khi bán được \(50\) sản phẩm đầu tiên là \(519\) triệu đồng.

c) Biết sự thay đổi của lợi nhuận khi doanh số tăng từ \(50\) lên \(a\) đơn vị sản phẩm lớn hơn \(517\) triệu đồng, khi đó giá trị nhỏ nhất của \(a\) là \(100\).

d) Sự thay đổi của lợi nhuận khi doanh số tăng từ \(50\) lên \(55\) đơn vị sản phẩm là \(49,79\) triệu đồng.

Cho hàm số \(f\left( x \right) = 1 + \frac{1}{x}\) có đồ thị \(\left( C \right)\) và hàm số \(g\left( x \right) = - \frac{1}{4}x + \frac{9}{4}\) có đồ thị \(\left( d \right)\) (xem hình bên).

a) \(\int {f\left( x \right){\rm{d}}x = x - \ln \left| x \right| + C} \) với \(C\) là hằng số.

b) Nếu \(f\left( x \right)\) có một nguyên hàm là hàm số \(F\left( x \right)\) và \(F\left( 1 \right) = 0\) thì \(F\left( 2 \right) = 1 + \ln 2\).

c) Hình phẳng \({H_1}\) (phần gạch chéo) giới hạn bởi đồ thị \(\left( C \right)\), đồ thị \(\left( d \right)\) và các đường \(x = 1,x = 4\) có diện tích là \({S_1} = \frac{{15}}{8} - \ln 4\).

d) Nếu \({S_1},{S_2}\) lần lượt là diện tích hình phẳng \({H_1}\) (phần gạch chéo) và \({H_2}\)(hình phẳng giới hạn bởi đồ thị \(\left( C \right)\), trục hoành và các đường \(x = 1,x = 4\)) thì \(\frac{{{S_1}}}{{{S_2}}} = \frac{5}{8}\).

PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\), biết \(f\left( x \right) = 16{x^3} - 15{x^2} + 2x\int\limits_1^2 {f\left( t \right){\rm{d}}t} - 21\). Giá trị của \(f\left( 2 \right)\) bằng bao nhiêu?

Một cái hồ lô trang trí được thiết kế phần chứa nước có thể tích bằng với thể tích của một vật thể \(\left( V \right)\) trong không gian. Biết rằng, điểm \(M\) thuộc \(\left( V \right)\) khi và chỉ khi \(MA \le \sqrt 2 \,{\rm{dm}}\) hoặc \(MB \le \sqrt 5 \,{\rm{dm}}\), trong đó \[A\] và \[B\] là hai điểm cố định, \[AB = 3\,\,{\rm{dm}}\]. Thể tích phần chứa nước của hồ lô đó là bao nhiêu lít? (làm tròn kết quả đến hàng phần chục).

Một viên đạn được bắn thẳng đứng lên trên từ độ cao \(2\,\,{\rm{m}}\) với vận tốc tại thời điểm \(t\) cho bởi công thức \(v\left( t \right) = 100 - 9,8t\,\,\left( {{\rm{m/s}}} \right)\) (\(t = 0\) là thời điểm viên đạn được bắn lên). Tìm độ cao (tính theo \({\rm{km}}\)) của viên đạn so với mặt đất ở thời điểm 1 giây sau khi viên đạn đạt độ cao lớn nhất (làm tròn kết quả đến hàng phần trăm).

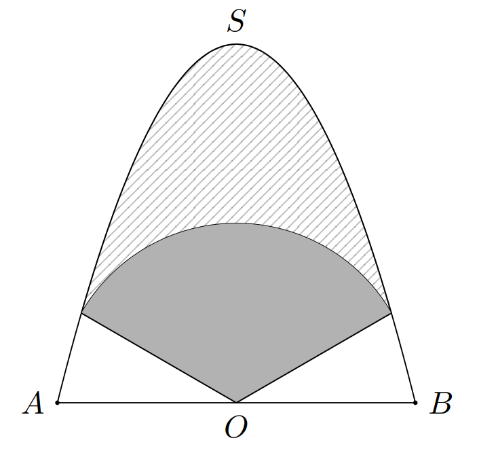
Để chuẩn bị quảng bá sản phẩm, người ta trang trí tấm pano dạng parabol như hình vẽ bên, biết \[OS = 8\,\,{\rm{m}}\], \[AB = 6\,\,{\rm{m}}\] với \[O\] là trung điểm của \[AB\]. Tấm pano được chia thành ba phần để trang trí với mức chi phí khác nhau: phần trên là phần kẻ sọc giá \(100\,000\) đồng/m², phần giữa là hình quạt tâm \[O\] bán kính \(3\,\,{\rm{m}}\) được tô đậm giá \(200\,000\) đồng/m², phần còn lại giá \(150\,000\) đồng/m². Tính tổng chi phí để trang trí tấm pano (đơn vị triệu đồng, kết quả làm tròn đến hàng phần trăm).

Nhà bác Ba có tất cả \(8\) cánh cửa sắt hình chữ nhật với chiều dài \(2\,{\rm{m}}\) và chiều rộng \(1\,{\rm{m}}\). Hai mặt của mỗi cánh cửa được thiết kế như hình vẽ bên. Trong đó, phần được tô đậm được sơn màu xanh, phần còn lại được sơn màu trắng. Mỗi phần sơn màu trắng có đường biên cong là một phần của parabol có đỉnh nằm trên cạnh của hình chữ nhật. Biết rằng chi phí để sơn màu xanh là \(120\) nghìn đồng\({\rm{/}}{{\rm{m}}^{\rm{2}}}\) và chi phí sơn màu trắng là \(110\) nghìn đồng\({\rm{/}}{{\rm{m}}^{\rm{2}}}\). Hỏi để sơn toàn bộ số cửa sắt trên, bác Ba phải tốn bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần trăm theo đơn vị triệu đồng).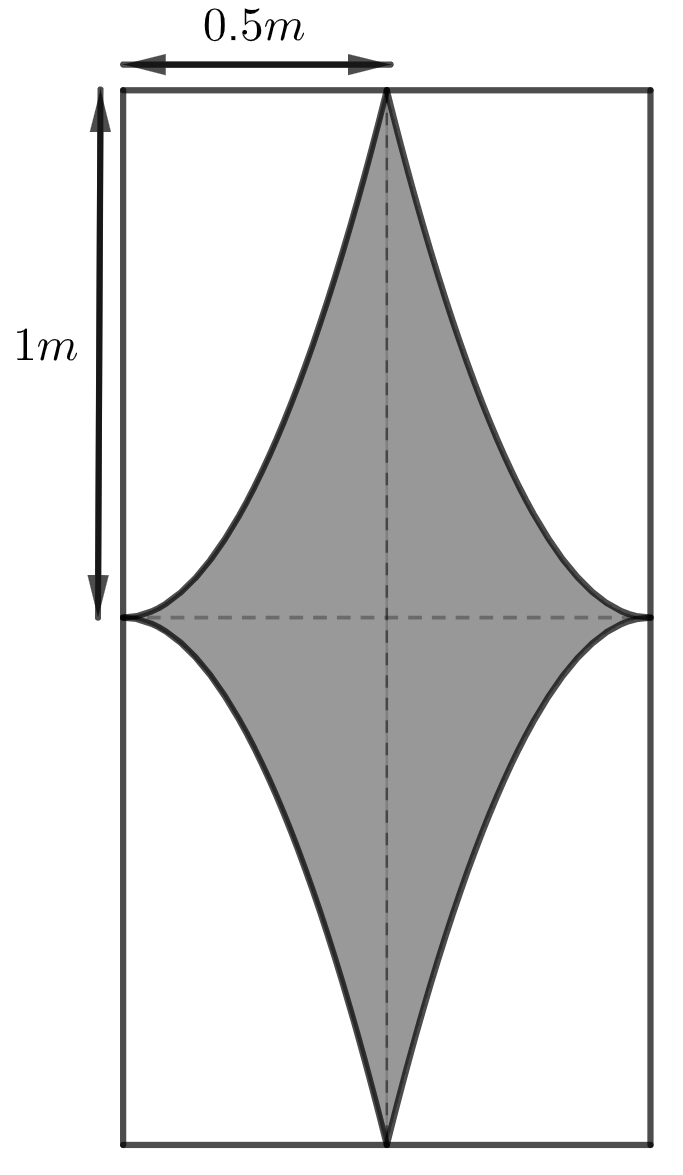

Một ly trà sữa dạng hình nón cụt, có đường kính đáy ly \(6\,\,{\rm{cm}}\), đường kính miệng ly \({\rm{9}}\,\,{\rm{cm}}\), chiều cao\(13,4\,\,{\rm{cm}}\), ở miệng ly có sử dụng một nắp đậy có hình dạng nửa mặt cầu và ở đỉnh của nửa mặt cầu này có một hình tròn có đường kính \(2\,{\rm{cm}}\) để cắm ống hút, mặt phẳng chứa hình tròn này song song với mặt phẳng chứa miệng ly (tham khảo hình vẽ bên).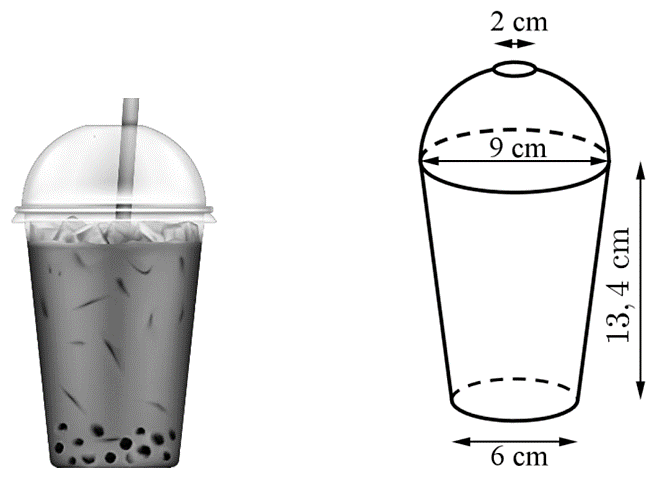

Thể tích bên trong của ly bao gồm cả thể tích của nắp là bao nhiêu centimét khối? (làm tròn kết quả đến hàng đơn vị).