Đề ôn luyện Toán theo Chủ đề 4. Nguyên hàm, tích phân và ứng dụng (Đề số 1)

Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \frac{{{x^2} - 3x + 2}}{x}\)là      

Biết \(\int\limits_0^9 {f\left( x \right){\rm{d}}x} = 37\) và \[\int\limits_0^9 {\left[ {3f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} = 61\]. Khi đó, \(\int\limits_0^9 {g\left( x \right){\rm{d}}x} \) bằng     

Cho \(\int\limits_0^1 {f\left( x \right){\rm{d}}x = 1} \) và \(\int\limits_0^2 {f\left( x \right){\rm{d}}x = - 4} \). Tích phân \[\int\limits_1^2 {f\left( x \right){\rm{d}}x} \] bằng     

Cho hàm số \(y = f\left( x \right)\). Biết rằng phần hình phẳng giới hạn bởi \({S_1}\) và \({S_2}\) (xem hình vẽ) có diện tích lần lượt bằng \(7\) và \(2\).

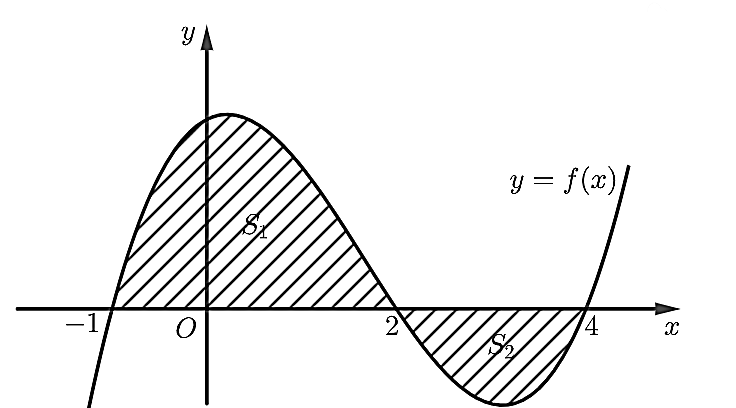
Tích phân \(\int\limits_{ - 1}^4 {f\left( x \right){\rm{d}}x} \) bằng

Họ nguyên hàm của hàm số \[f\left( x \right) = {\sin ^2}x\] là     

Gọi \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right) = 2x - \frac{1}{x}\] thoả mãn \[F\left( 1 \right) = 1\]. Tính \[F\left( { - 1} \right)\].     

Họ các nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{{x^3}}}\) là     

Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(c\) là số thực tùy ý thuộc đoạn \(\left[ {a;b} \right]\). Nếu \(\int\limits_a^b {f\left( x \right){\rm{d}}x = 3} \) và \(\int\limits_a^c {f\left( x \right){\rm{d}}x = 8} \) thì tích phân \(\int\limits_c^b {f\left( x \right){\rm{d}}x} \) bằng     

Biết rằng \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {1;4} \right]\) và \(F\left( 4 \right) = 9\), \(F\left( 1 \right) = 3\). Giá trị của \(\int\limits_1^4 {\left[ {f\left( x \right) + 2} \right]{\rm{d}}} x\) bằng     

Nếu \(\int\limits_{ - 3}^1 {f\left( x \right)} \,{\rm{d}}x = - 2\) thì \(\int\limits_{ - 3}^1 {\left[ {2 - 5f\left( x \right)} \right]} \,{\rm{d}}x\) bằng     

Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị \(y = 2x - {x^2}\) và trục hoành. Thể tích vật thể tròn xoay sinh ra khi cho \(\left( H \right)\) quay quanh trục hoành bằng     

PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

 Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = 8{x^3} + \sin x,\forall x \in \mathbb{R}\). Biết \(f\left( 0 \right) = 3\).

a) Hàm số \(y = f\left( x \right)\) là một nguyên hàm của hàm số \(f'\left( x \right)\).

b) \(f\left( x \right) = 2{x^4} - \cos x + 3\).

c) \(\int {f\left( x \right){\rm{d}}x = \frac{2}{5}{x^5} - \sin x + 3x + C} \), với \(C\)là hằng số.

d) Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) thoả \(F\left( 0 \right) = 2\). Khi đó \(F\left( 1 \right) = \frac{{32}}{5} - \sin 1\).

Một công ty thiết kế mẫu huy hiệu để tặng cho khách hàng thân thiết của mình (xem hình vẽ bên). Trong đó \(ABCD\)là hình vuông có cạnh bằng \(4\,{\rm{cm}}\), các đường cong \(AOD\)và \(BOC\) là một phần của các parabol đỉnh \(O\). Với hệ trục tọa độ \(Oxy\) (đơn vị trên mỗi trục tọa độ là centimét) thì điểm \(A\) có tung độ bằng \(1\). Biết phần tô đậm trong hình vẽ được phủ vàng với chi phí \(1\)một triệu đồng/\(1\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\), phần còn lại được phủ bạc với chi phí 300 nghìn đồng/\(1\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\), các chi phí còn lại là 500 nghìn đồng.

a) Parabol chứa đường cong \(AOD\) có phương trình là \(y = \frac{1}{{16}}{x^2}\).

b) Parabol chứa đường cong \(BOC\) có phương trình là \(y = - \frac{3}{4}{x^2}\).

c) Diện tích phần tô đậm trong hình vẽ lớn hơn \(5,5\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).

d) Chí sản xuất \(1\) chiếc huy hiệu trên nhỏ hơn \(9\) triệu đồng.

Cho một chất điểm chuyển động theo quy luật vận tốc \[v\left( t \right)\]( đơn vị: \[{\rm{m/s}}\]) có đồ thị như hình vẽ bên. Trong đó đồ thị có dạng các đoạn thẳng tương ứng theo thời gian \[t\] giây khi \[0 \le t \le 3\], \[8 \le t \le 15\] và có dạng đường parabol tương ứng thời gian \[t\] giây khi \[3 \le t \le 8\].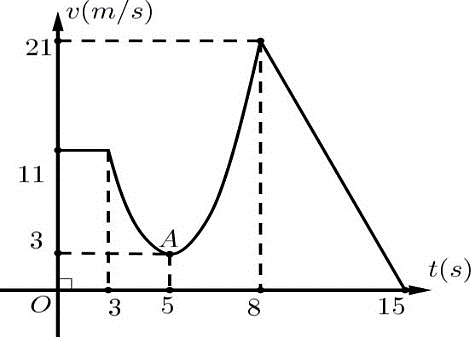

a)Vận tốc của chất điểm tại thời điểm\[t = 15\] là \[v\left( {15} \right) = 21\,\,\left( {{\rm{m/s}}} \right)\].

b)Quãng đường mà chất điểm đi được trong thời gian \[3\] giây đầu \[\left( {0 \le t \le 3} \right)\] là \(S = \int\limits_0^3 {11\,{\rm{d}}t\,\,\,{\rm{(m)}}} \).

c)Quãng đường mà chất điểm đi được trong khoảng thời gian \[7\] giây cuối \[\left( {8 \le t \le 15} \right)\] là \(73,5\,\,{\rm{m}}\).

d)Vận tốc trung bình \({v_{tb}}\) của chất điểm trong thời gian \[t\] giây \[\left( {3 \le t \le 8} \right)\] thỏa mãn \({v_{tb}} < 7\,\,\left( {{\rm{m/s}}} \right)\).

Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{x}\).

a) \(\int {f\left( x \right)} \,{\rm{d}}x = 2x + \ln \left| x \right| + C\).

b) Gọi \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) và thỏa mãn \(F\left( 1 \right) = 3\).

Khi đó \(F\left( x \right) = 2x + \ln \left| x \right| + 1\).

c) \(\int {f'\left( {2x} \right)} \,{\rm{d}}x = \frac{{ - 1}}{{4x}} + C\).

d) Gọi \(G\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Biết \(G\left( 2 \right) = 1\) và \(G\left( 5 \right) + G\left( { - 5} \right) = 0\). Ta tìm được \(G\left( { - 10} \right) = a\ln 10 + b\ln 5 + c\ln 2 + d\), với \(a,\,b,\,c\) là các số hữu tỷ. Ta có \(a + b + c + d = - 19\).

PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.

Người ta cho một chiếc xe điện mô hình chạy thử nghiệm trên một đường thẳng trong 24 giây với vận tốc \[v\left( t \right) = \left\{ \begin{array}{l}\frac{1}{2}t\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\;\;0 \le t \le 8\\4\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{khi}}\,\,\;8 < t < 16\\ - \frac{1}{2}t + 12\;\,\,\,\,\,{\rm{khi}}\;\;16 \le t \le 24\end{array} \right.\](decimét/giây), trong đó \[t\]là khoảng thời gian tính bằng giây kể từ lúc xe bắt đầu chuyển động. Trong 24 giây chạy thử nghiệm đó, chiếc xe mô hình đi được quãng đường bao nhiêu decimét?

Hình vẽ bên cho biết một miền D (được tô đậm) nằm trong hình vuông cạnh bằng 4, miền D này gồm những điểm có khoảng cách tới tâm hình vuông nhỏ hơn hoặc bằng khoảng cách tới cạnh gần nhất của hình vuông.

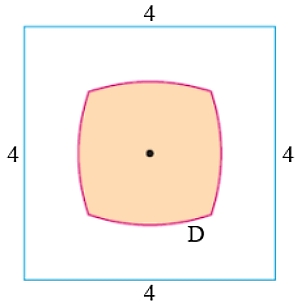
Tính diện tích miền D, với kết quả làm tròn đến chữ số thập phân thứ nhất.

Trong các làng nghề chế tạo đá mỹ nghệ, người ta làm được nhiều đồ trang sức bằng đá rất đẹp. Một người thợ thủ công chế tạo vòng đeo tay hình tròn bằng đá xanh, biết rằng bán kính vòng ngoài của vòng là \(7\,{\rm{cm}}\), bán kính vòng trong là \(5\,{\rm{cm}}\) (hình vẽ). Tính thể tích của chiếc vòng (theo đơn vị đo là centimét khối và làm tròn kết quả đến hàng đơn vị).

Cho hai khối trụ có bán kính đáy bằng \(3\) và có trục là hai đường thẳng cắt nhau và vuông góc với nhau (xem hình vẽ). Gọi \(\left( H \right)\) là phần giao nhau của hai khối trụ đó. Tính thể tích của \(\left( H \right)\).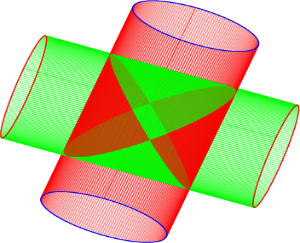

Trong một trò chơi điện tử, hai bạn Tít và Mít thi xem ai chạy được quãng đường xa hơn. Tít chạy với vận tốc \[{v_T}\,\left( t \right) = 5\sqrt t \]\[\left( {{\rm{km/h}}} \right)\], quãng đường Mít chạy được cho bởi phương trình \[{s_M}\left( t \right) = 5t - \frac{5}{{2\pi }}\sin \,\left( {2\pi t} \right)\]\[\left( {{\rm{km}}} \right)\](với \[t\] là thời gian tính theo giờ). Nếu cuộc đua kết thúc khi Tít hoặc Mít chạy được \[10{\kern 1pt} {\kern 1pt} \,{\rm{km}}\]đầu tiên thì khoảng cách giữa hai bạn là bao nhiêu kilômét (kết quả làm tròn đến hàng phần trăm).

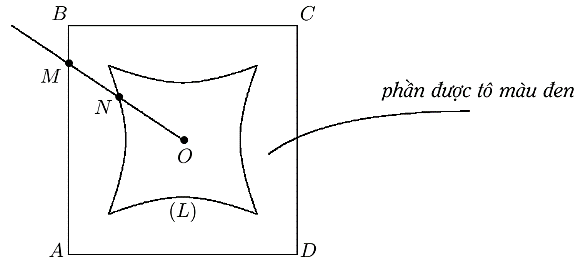
Người nghệ sĩ vẽ một bông hoa không màu trên một miếng bìa hình vuông \(ABCD\) tâm \(O\) bằng một đường cong kín \(\left( L \right)\) rồi tô màu đen phần bên ngoài đường cong này của hình vuông (tham khảo hình vẽ). Nếu điểm \(M\) thuộc cạnh của hình vuông \(ABCD\) và tia \(OM\) cắt \(\left( L \right)\) tại điểm \(N\) thì \(MN = 2\,{\rm{dm}}\). Biết rằng \(AB = 8\,\,{\rm{dm,}}\) phần được nghệ sĩ tô màu đen có diện tích bằng bao nhiêu centimet vuông (làm tròn kết quả đến hàng đơn vị)?