12 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Họ các nguyên hàm của hàm số \(f\left( x \right) = 3{e^x}\) là
\(3{e^x}\).
\(3x{e^x} + C\).
\(3{e^x} + C\).
\( - 3{e^x} + C\).
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \frac{{{x^2} - 3x + 2}}{x}\)là
\(\frac{1}{2}{x^2} - 3x + C\).
\(\frac{1}{2}{x^2} - 3x + 2\ln \left| x \right| + C\).
\(\frac{1}{2}{x^2} - 2\ln x + C\).
\(\ln \left( {\frac{{{x^2} - 3x + 2}}{x}} \right) + C\).
Biết \(\int\limits_0^9 {f\left( x \right){\rm{d}}x} = 37\) và \[\int\limits_0^9 {\left[ {3f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} = 61\]. Khi đó, \(\int\limits_0^9 {g\left( x \right){\rm{d}}x} \) bằng
\( - 25\).
\(25\).
\( - 86\).
\(86\).
Cho \(\int\limits_0^1 {f\left( x \right){\rm{d}}x = 1} \) và \(\int\limits_0^2 {f\left( x \right){\rm{d}}x = - 4} \). Tích phân \[\int\limits_1^2 {f\left( x \right){\rm{d}}x} \] bằng
\(5\).
\( - 3\).
\( - 5\).
\(3\).
Cho hàm số \(y = f\left( x \right)\). Biết rằng phần hình phẳng giới hạn bởi \({S_1}\) và \({S_2}\) (xem hình vẽ) có diện tích lần lượt bằng \(7\) và \(2\).
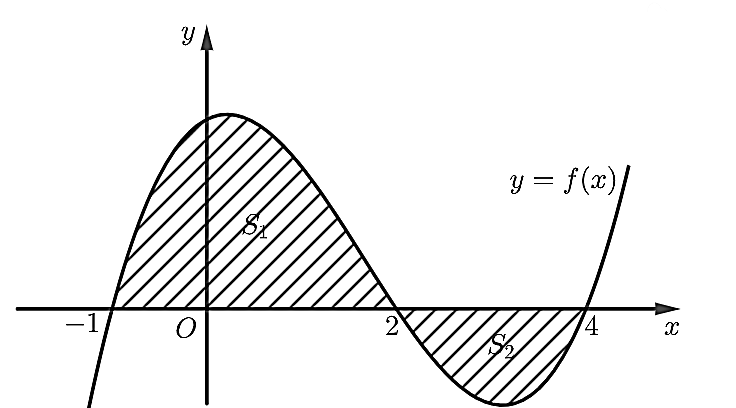
Tích phân \(\int\limits_{ - 1}^4 {f\left( x \right){\rm{d}}x} \) bằng
\(9\).
\( - 5\).
\( - 9\).
\(5\).
Họ nguyên hàm của hàm số \[f\left( x \right) = {\sin ^2}x\] là
\(\frac{x}{2} - \frac{{\sin 2x}}{4} + C\).
\(\frac{x}{2} + \frac{{\sin 2x}}{4} + C\).
\(\frac{x}{2} - \frac{{\sin 2x}}{2} + C\).
\(\frac{x}{2} + \frac{{\sin 2x}}{2} + C\).
Gọi \[F\left( x \right)\] là một nguyên hàm của hàm số \[f\left( x \right) = 2x - \frac{1}{x}\] thoả mãn \[F\left( 1 \right) = 1\]. Tính \[F\left( { - 1} \right)\].
\[F\left( { - 1} \right) = 1\].
\[F\left( { - 1} \right) = 2\].
\[F\left( { - 1} \right) = - 1\].
\[F\left( { - 1} \right) = 0\].
Họ các nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{{x^3}}}\) là
\( - \frac{3}{{{x^4}}} + C\).
\( - \frac{1}{{{x^2}}} + C\).
\( - \frac{1}{{2{x^2}}} + C\).
\( - \frac{1}{{4{x^4}}} + C\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(c\) là số thực tùy ý thuộc đoạn \(\left[ {a;b} \right]\). Nếu \(\int\limits_a^b {f\left( x \right){\rm{d}}x = 3} \) và \(\int\limits_a^c {f\left( x \right){\rm{d}}x = 8} \) thì tích phân \(\int\limits_c^b {f\left( x \right){\rm{d}}x} \) bằng
11.
\( - 5\).
5.
\( - 11\).
Biết rằng \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {1;4} \right]\) và \(F\left( 4 \right) = 9\), \(F\left( 1 \right) = 3\). Giá trị của \(\int\limits_1^4 {\left[ {f\left( x \right) + 2} \right]{\rm{d}}} x\) bằng
\(0\).
\(8\).
\( - 4\).
\(12\).
Nếu \(\int\limits_{ - 3}^1 {f\left( x \right)} \,{\rm{d}}x = - 2\) thì \(\int\limits_{ - 3}^1 {\left[ {2 - 5f\left( x \right)} \right]} \,{\rm{d}}x\) bằng
\(18\).
\(6\).
\(12\).
\( - 4\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị \(y = 2x - {x^2}\) và trục hoành. Thể tích vật thể tròn xoay sinh ra khi cho \(\left( H \right)\) quay quanh trục hoành bằng
\(\frac{{16}}{{15}}\).
\(\frac{4}{3}\).
\(\frac{{16\pi }}{{15}}\).
\(\frac{{4\pi }}{3}\).
