12 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên sau:
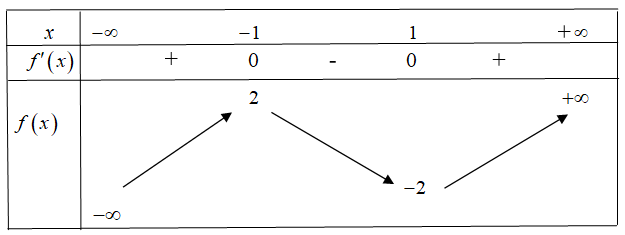
Giá trị cực tiểu của hàm số đã cho bằng:
\(2\).
\( - 2\).
\( - 1\).
\(1\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong như hình vẽ bên. Hàm số đã cho nghịch biến trong khoảng nào dưới đây?
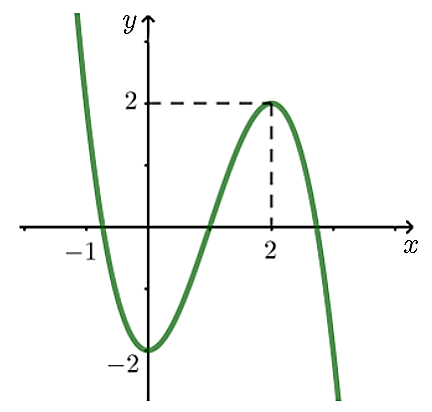
\(\left( { - 2;2} \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( {0;2} \right)\).
\(\left( { - \infty ;2} \right)\).
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \[\mathbb{R}\], có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?
Giá trị nhỏ nhất của hàm số đã cho là \[ - 1\].
Đồ thị hàm số \[f\left( x \right)\] có đúng hai điểm cực trị.
Giá trị lớn nhất của hàm số đã cho là \[0\].
Đồ thị hàm số \[f\left( x \right)\] có đúng một điểm cực tiểu.
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\left( {c \ne 0\,;\,ad - bc \ne 0} \right)\] có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số đã cho là
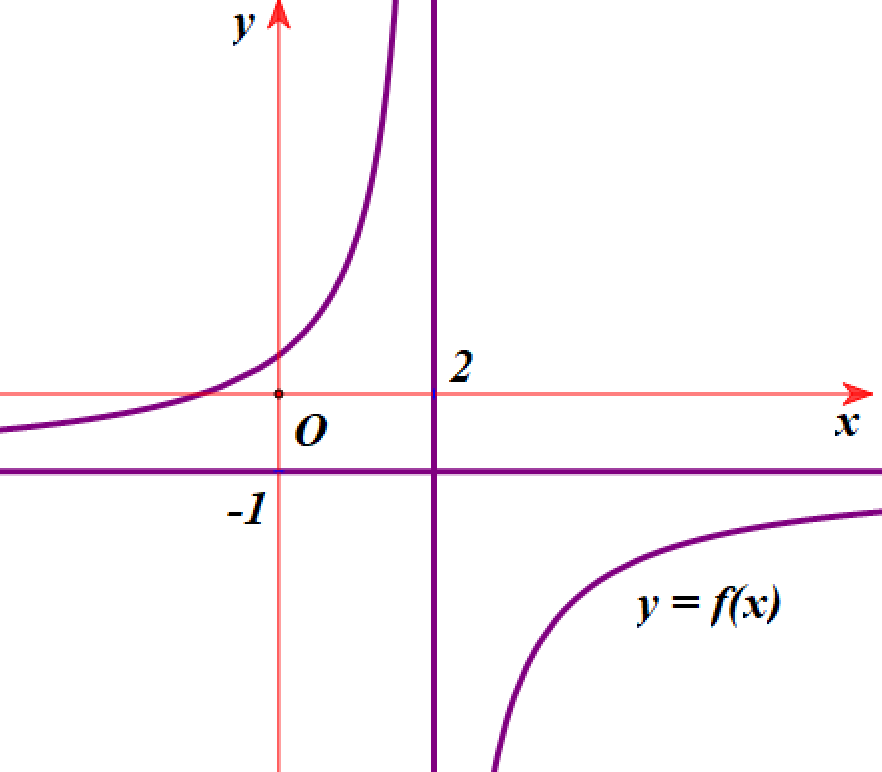
\[y = - 1\].
\[y = 2\].
\[x = - 1\].
\[x = 2\].
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
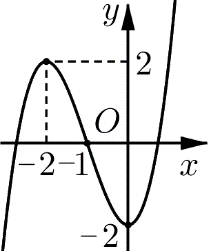
\(y = - {x^3} - 3{x^2} - 2.\)
\(y = {x^3} + 3{x^2} - 2.\)
\(y = - {x^3} + 3{x^2} - 2.\)
\(y = {x^3} - 3{x^2} - 2.\)
Tìm giá trị nhỏ nhất của hàm số \(y = - x + 3 - \frac{1}{{x + 2}}\) trên nửa khoảng \(\left[ { - 4; - 2} \right)\) .
\(\mathop {\min }\limits_{\left[ { - 4; - 2} \right)} y = 5\).
\(\mathop {\min }\limits_{\left[ { - 4; - 2} \right)} y = 4\).
\(\mathop {\min }\limits_{\left[ { - 4; - 2} \right)} y = 7\).
\(\mathop {\min }\limits_{\left[ { - 4; - 2} \right)} y = \frac{{15}}{2}\).
Cho hàm số \(y = f\left( x \right)\) xác định, có đạo hàm trên \(\mathbb{R}\) và \(f'\left( x \right)\) có đồ thị như hình vẽ dưới.
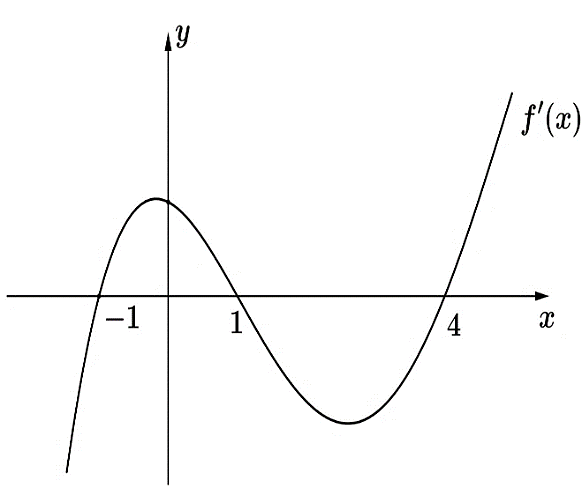
Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng nào dưới đây?
\[\left( {1;4} \right)\].
\[\left( { - 1;1} \right)\].
\[\left( {1; + \infty } \right)\].
\[\left( { - \infty ; - 1} \right)\].
Đồ thị hàm số \(y = \frac{{ - {x^2} + 4x - 3}}{{x + 2}}\) có đường tiệm cận xiên là
Đường thẳng \(y = - 1\).
Đường thẳng \(y = - x + 6\).
Đường thẳng \(x = - 2\).
Đường thẳng \(y = - x\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {{x^2} + x - 2} \right){\left( {x - 1} \right)^4}\) với mọi \(x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(3\).
\(2\).
\(1\).
\(0\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
\(3\).
\(2\).
\(1\).
\(0\).
Giá trị lớn nhất của hàm số \[f\left( x \right) = {x^3} - 3{x^2} - 9x + 10\] trên đoạn \[\left[ { - 2\,;\,2} \right]\] là
\[17\].
\[10\].
\[15\].
\[ - 12\].
Đồ thị hàm số \[y = {x^3} - 6{x^2} + 9x - 1\] có toạ độ điểm cực đại là
\(\left( {3\,;0} \right)\).
\(\left( {3\,;1} \right)\).
\(\left( {1\,;4} \right)\).
\(\left( {1\,;3} \right)\).
