Đề ôn luyện Toán theo Chủ đề 3. Đạo hàm và khảo sát hàm số (Đề số 1)
22 câu hỏi
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?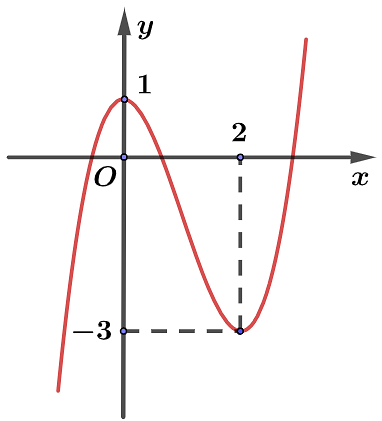
\(\left( { - \infty ;0} \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( { - 3;1} \right)\).
\(\left( {0;2} \right)\).
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] (với \[c \ne 0,\,ad - bc \ne 0\]) có đồ thị như hình vẽ bên. Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là: 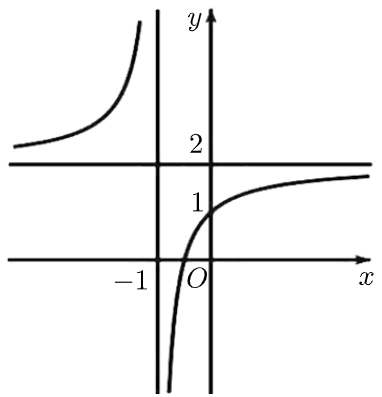
\[x - 2 = 0\].
\[x + 1 = 0\].
\[y + 1 = 0\].
\[y - 2 = 0\].
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
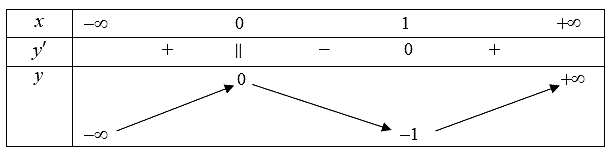
Khẳng định nào sau đây là khẳng định đúng?
Hàm số có đúng một cực trị.
Hàm số có giá trị lớn nhất bằng \(0\) và giá trị nhỏ nhất bằng \( - 1\).
Hàm số có giá trị cực tiểu bằng \(1\).
Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 1\).
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 4x - 7}}{{x - 2}}\) là
\(y = x - 6\).
\(y = - x - 6\).
\(y = - x + 6\).
\(y = x + 6\).
Cho hàm đa thức \[y = f\left( x \right)\]. Đồ thị hàm số \[y = f'\left( x \right)\] là đường cong như hình vẽ bên dưới. Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?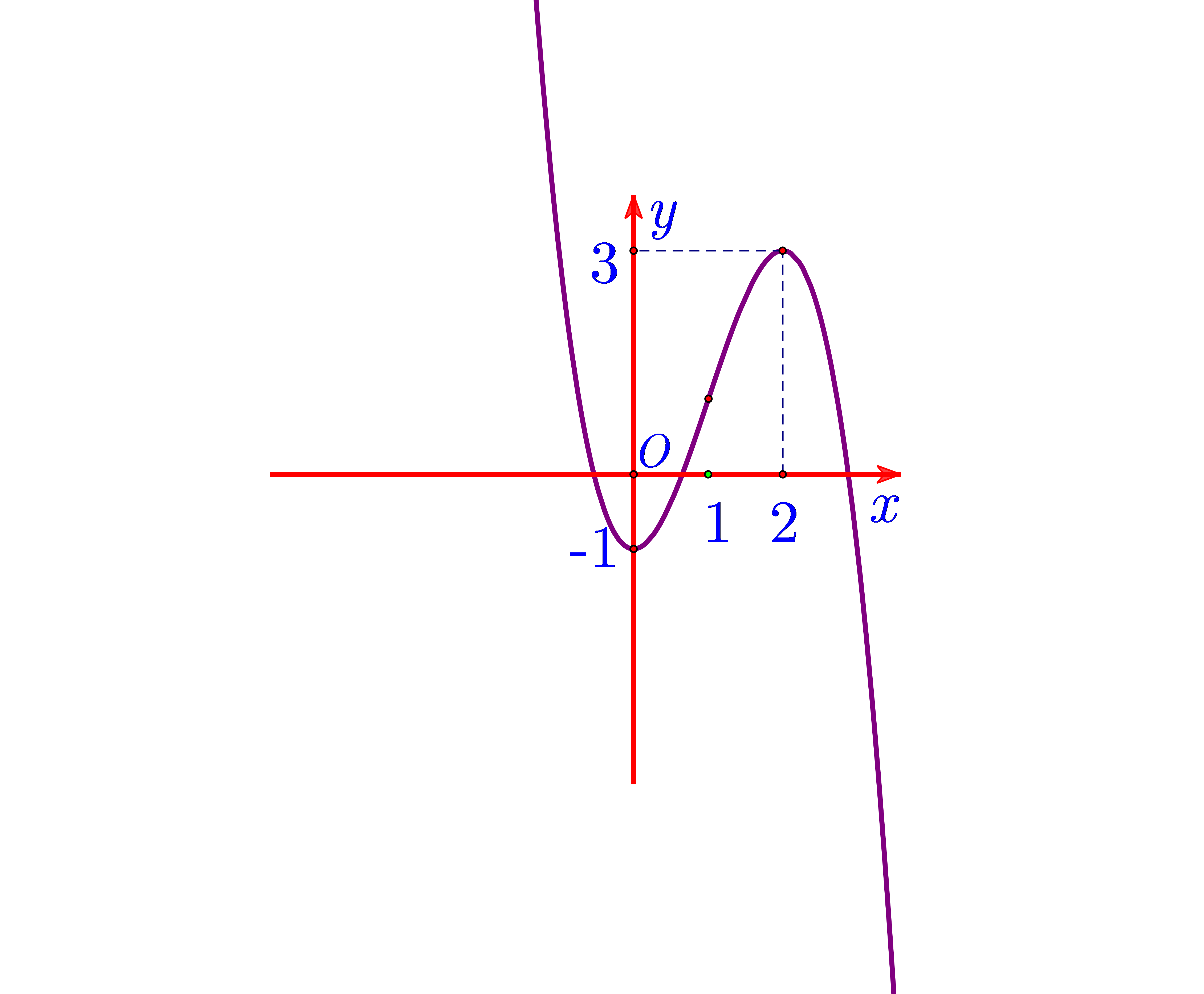
\(3\).
\(1\).
\(2\).
\(0\).
Giá trị lớn nhất của hàm số \(y = {x^3} - 3x + 4\) trên đoạn \(\left[ { - 2;0} \right]\) bằng
\(2\).
\(4\).
\(12\).
\(6\).
Giá trị \(m\) để tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x + 2m - 1}}{{x + m}}\) đi qua điểm \(M\left( {3\,;\,1} \right)\) là
\(m = - 3\).
\(m = - 1\).
\(m = 2\).
\(m = 3\).
Biết đường thẳng \[y = x - 2\] cắt đồ thị hàm số \[y = \frac{{2x + 1}}{{x - 1}}\] tại hai điểm phân biệt \[A\] và \[B\] có hoành độ lần lượt là \[{x_A},{x_B}\]. Giá trị của biểu thức \[{x_A} + {x_B}\] bằng
\[3\].
\[2\].
\[1\].
\[5\].
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 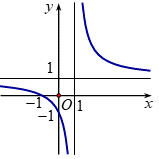
\(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = {x^3} - 3x - 1\).
Cho hàm số \(f\left( x \right) = \frac{{m{x^2} + nx + p}}{{qx + r}}\) có bảng biến thiên như hình vẽ bên dưới:
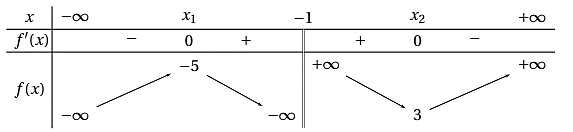
Ta có \(I\) là tâm đối xứng của đồ thị hàm số \(y = f\left( x \right)\). Tìm toạ độ \(I\).
\(I\left( { - 2\,;\,1} \right)\).
\(I\left( { - 1\,;\,1} \right)\) .
\(I\left( { - 1\,;\,0} \right)\).
\(I\left( { - 1\,; - 1} \right)\).
Hàm số nào dưới đây đồng biến trên khoảng \(\left( {0;2} \right)\)?
\(y = - {x^3} - 3x\).
\(y = \frac{{x - 2}}{{x - 1}}\).
\(y = - {x^3} + 5{x^2}\).
\(y = \frac{{x - 1}}{{x - 2}}\).
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) đạt cực tiểu tại điểm \(x = 1\) và \(f\left( 1 \right) = - 3\). Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính \(T = 3a + b - c\).
\(T = 1\).
\(T = 9\).
\(T = - 4\).
\(T = - 2\).
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(f\left( x \right) = \ln x - x\).
a) Tập xác định của hàm số\(f\left( x \right)\) là \(\mathbb{R}\).
b) Ta có \(f'\left( x \right) = \frac{1}{x} - 1\).
c) Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
d)Hàm số \(g\left( x \right) = {e^{f\left( x \right)}}\) nghịch biến trên khoảng\(\left( {1; + \infty } \right)\).
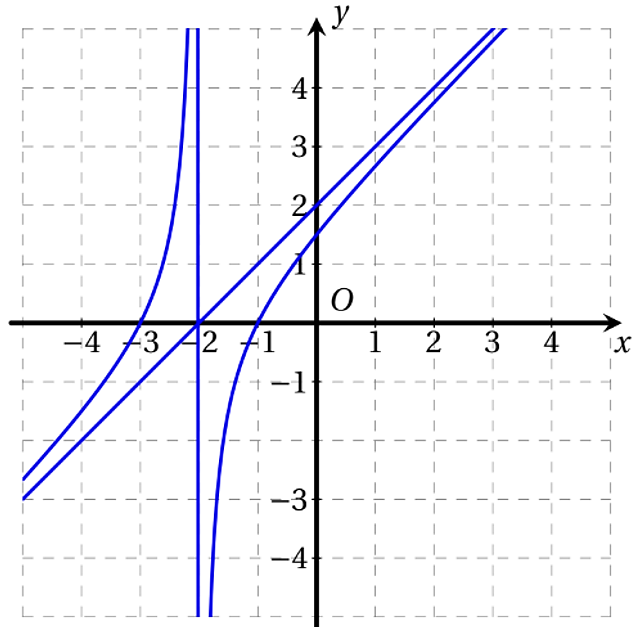
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\,\,\left( {a \ne 0} \right)\) có đồ thị như hình vẽ.
a) Hàm số đã cho có hai cực trị trái dấu. b) \(f\left( 5 \right) = 52\). c) Gọi \(d\) là đường thẳng đi qua các điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Khoảng cách từ điểm \(O\) đến đường thẳng \(d\) bằng \(\frac{2}{5}\). d) Hàm số \(g\left( x \right) = f\left( x \right) - \left( {3x - 2{x^3}} \right)\) đạt cực tiểu tại \(x = - 1\). |
|
Cho hàm số \(y = \frac{{{x^2} + 10x + 10}}{{x + 1}}\) có đồ thị \(\left( C \right)\).
a) Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
b) Tiệm cận đứng của đồ thị \(\left( C \right)\) là \(x = - 1\).
c) Tiệm cận xiên của đồ thị \(\left( C \right)\) là \(y = x\).
d) Gọi \(A,B\) là hai điểm cực trị của đồ thị hàm số \(\left( C \right)\). Khi đó diện tích tam giác \(OAB\) bằng \(12\).
Kinzhal là tên lửa siêu thanh có khả năng mang đầu đạn hạt nhân, được phóng đi từ các hệ thống phóng mặt đất. Giả sử rằng Kinzhal (không gắn với động cơ) được bắn lên cao theo phương trình \[s\left( t \right) = 1960t - 49{t^2}\] trong đó \[t\] là thời gian (\[t > 0\], đơn vị giây) và \[s\left( t \right)\] là khoảng cách của tên lửa so với mặt đất được tính bằng kilômet.
a) Khoảng cách của tên lửa so với mặt đất tại thời điểm \[t = 2\,\left( {\rm{s}} \right)\] là \[s = 5\,008\,\,\left( {{\rm{km}}} \right)\].
b) Khoảng cách của tên lửa so với mặt đất tại thời điểm vận tốc bằng \(0\) là \(19\,600\,\,\left( {{\rm{km}}} \right)\).
c) Vận tốc tức thời của tên lửa tại thời điểm \[t = 2\,\left( {\rm{s}} \right)\] là \[5\,008,8\,\,\left( {{\rm{km/s}}} \right)\].
d) Quãng đường lớn nhất mà tên lửa có thể đạt được là\[19\,600\,\,\left( {{\rm{km}}} \right)\].
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = \,\left( {{x^2} - 1} \right)\left( {x - 4} \right)\] với mọi \[x \in \mathbb{R}\]. Hàm số \[g\left( x \right)\, = \,f\left( {3 - x} \right)\] có bao nhiêu điểm cực đại?
Người ta thống kê được chi phí sửa chữa, vận hành máy móc trong một năm của một xưởng sản xuất được tính bởi công thức \(f\left( x \right) = \frac{{2000x - 1500}}{{35x + 5}}\)(triệu đồng). Biết \(x\) là số năm kể từ lúc máy móc vận hành lần đầu tiên, số năm càng nhiều thì chi phí càng cao. Khi số năm \(x\) đủ lớn thì chi phí vận hành máy móc trong một năm gần với số nào? (làm tròn kết quả đến 1 chữ số thập phân sau dấu phẩy).
Một nhà địa chất học đang ở tại điểm \(A\) trên sa mạc. Anh ta muốn đến điểm \(B\) và cách \(A\) một đoạn là \(100\,{\rm{km}}\). Trong sa mạc thì xe anh ta chỉ có thể di chuyển với vận tốc là \(30\,{\rm{km/h}}\). Nhà địa chất phải đến được điểm \(B\) sau \(3\) giờ.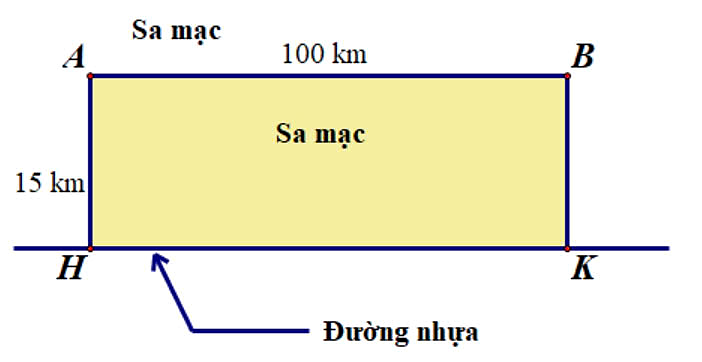
Vì vậy, nếu anh ta đi từ \(A\) đến \(B\) sẽ không thể đến đúng giờ được. Sau khi khảo sát địa hình nhà địa chất phát hiện ra một con đường song song với đường nối \(A\) và \(B\) và cách \(AB\) một đoạn \(15\,{\rm{km}}\). Trên con đường đó thì xe nhà địa chất này có thể di chuyển với vận tốc \(50\,{\rm{km/h}}\). Thời gian ngắn nhất để nhà địa chất di chuyển từ \(A\) đến \(B\) là bao nhiêu phút?
Một xưởng in có \(15\) máy in được cài đặt tự động và giám sát bởi một kỹ sư, mỗi máy in có thể in được \(30\) ấn phẩm trong \(1\) giờ, chi phí cài đặt và bảo dưỡng cho mỗi máy in cho \(1\) đợt hàng là \(48\,000\) đồng, chi phí trả cho kỹ sư giám sát là \(24\,000\)đồng/giờ. Đợt hàng này xưởng in nhận \(6000\) ấn phẩm thì số máy in cần sử dụng để chi phí in ít nhất là bao nhiêu?
Để tạo một kiện hàng dạng hình lăng trụ đứng với đáy là hình chữ nhật có chiều dài gấp đôi chiều rộng, người ta dùng các thanh gỗ ghép khít đóng lại với nhau. Biết rằng, dung tích kiện hàng bằng \(9\,{{\rm{m}}^{\rm{3}}}\) và giá thành \(1\,{{\rm{m}}^{\rm{2}}}\) gỗ sử dụng là \(200\,000\) đồng.
Hỏi sau khi hoàn thành kiện hàng đó, người ta cần bỏ ra ít nhất bao nhiêu triệu đồng? (diện tích các mép giữa hai mặt kề nhau không đáng kể).
Cho hàm số \(y = f\left( x \right) = \frac{{a{x^2} + bx + 3}}{{x + c}}\) với \(a \ne 0,\) có đồ thị là đường cong như hình vẽ bên. Giá trị của biểu thức \(S = a + b + c\) bằng bao nhiêu?