Đề ôn luyện Toán Chương 7. Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian (đề số 1)
22 câu hỏi
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):2x - y + 3z - 4 = 0\). Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) có tọa độ là
\(\left( {3; - 1;2} \right)\).
\(\left( {2; - 1;3} \right)\)..
\(\left( { - 1;2;3} \right)\).
\(\left( {2;1;3} \right)\).
Trong không gian \[Oxyz\], cho đường thẳng \[d\]có phương trình \[\frac{{x + 1}}{{ - 2}} = \frac{{2 - y}}{3} = \frac{z}{2}\] . Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng \[d\]?
\[{\vec u_1} = \left( { - 2; - 3;2} \right)\].
\[{\vec u_2} = \left( { - 2;3;2} \right)\].
\[{\vec u_3} = \left( {2; - 3; - 2} \right)\].
\[{\vec u_4} = \left( { - 2; - 3; - 2} \right)\].
Trong không gian \[Oxyz\], cho đường thẳng \[d:\frac{{x - 1}}{4} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 7}}\]. Phương trình mặt phẳng đi qua \[A\left( {1;2;3} \right)\]và vuông góc với đường thẳng \[d\] là
\[4x + 3y + 7z - 11 = 0\].
\[4x + 3y + 7z + 11 = 0\].
\[4x + 3y - 7z + 11 = 0\].
\[4x + 3y - 7z - 11 = 0\].
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;3; - 2} \right),B\left( {2; - 2; - 1} \right)\). Phương trình đường thẳng \(AB\) là
\(\frac{{x + 1}}{1} = \frac{{y + 3}}{{ - 5}} = \frac{{z - 2}}{1}\).
\(\frac{{x - 1}}{1} = \frac{{y - 3}}{3} = \frac{{z + 2}}{{ - 2}}\).
\(\frac{{x - 2}}{1} = \frac{{y + 2}}{{ - 5}} = \frac{{z + 1}}{1}\).
\(\frac{{x + 2}}{1} = \frac{{y - 2}}{{ - 5}} = \frac{{z - 1}}{1}\).
Trong không gian \(Oxyz\), phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1\,;\,2\,;\,1} \right)\)và đi qua điểm \(A\left( {0\,;\,4\,;\, - 1} \right)\)là
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 3\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\).
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 3\).
Trong không gian \[Oxyz\], đường thẳng đi qua điểm \[A\left( {1;1;1} \right)\] và vuông góc với mặt phẳng \[\left( {Oxy} \right)\] có phương trình tham số là:
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1\\z = 1\end{array} \right.\left( {t \in \mathbb{R}} \right)\].
\[\left\{ \begin{array}{l}x = 1\\y = 1\\z = 1 + t\end{array} \right.\left( {t \in \mathbb{R}} \right)\].
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1\\z = 1\end{array} \right.\left( {t \in \mathbb{R}} \right)\].
\[\left\{ \begin{array}{l}x = 1 + t\\y = 1 + t\\z = 1\end{array} \right.\left( {t \in \mathbb{R}} \right)\].
Trong không gian \(Oxyz\), khoảng cách giữa hai mặt phẳng \(\left( P \right):x + 2y + 2z - 10 = 0\) và \(\left( Q \right):x + 2y + 2z - 3 = 0\) bằng
\(\frac{2}{3}\).
\(\frac{7}{3}\).
\(\frac{8}{3}\).
\(\frac{4}{3}\).
Trong không gian \[Oxyz\], đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{2}\) đi qua điểm nào dưới đây?
\(P\left( {1; - 2;3} \right)\).
\(M\left( { - 1;2; - 3} \right)\).
\(Q\left( {2; - 1;2} \right)\).
\(N\left( { - 2;1; - 2} \right)\).
Trong không gian \(Oxyz\), mặt cầu \(\left( S \right)\) có phương trình \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 4\)có bán kính bằng
16.
8.
2.
4.
Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):x + y + 4z - 1 = 0\] và \[\left( Q \right):x - z = 0\]. Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng
\(0^\circ \).
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có phương trình \(x + y + 2z + 2 = 0\). Mặt phẳng nào sau đây song song với mặt phẳng \(\left( \alpha \right)\)?
\(\left( S \right):x + y + 2z - 1 = 0\)
\(\left( Q \right):x + y - 2z - 2 = 0\).
\(\left( P \right):x - y + 2z - 2 = 0\).
\(\left( R \right):x + y - 2z + 1 = 0\).
Trong không gian \(Oxyz\), khoảng cách từ điểm \(A\left( {1;3; - 2} \right)\) đến mặt phẳng \(\left( {Oxy} \right)\) bằng
\(2\).
\(\sqrt {14} \).
\(3\).
\(1\).
Trong không gian \[Oxyz\], cho mặt phẳng \(\left( P \right):x - 2y + z = 0\), đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + t\\y = - 3t\\z = 1 + t\end{array} \right.\)và hai điểm \(A\left( {2;1;0} \right),B\left( {2; - 3;4} \right)\).
a) Điểm \(A\) thuộc mặt phẳng \(\left( P \right)\).
b) Hoành độ giao điểm của đường thẳng \(d\)và mặt phẳng \(\left( P \right)\) bằng \(\frac{{ - 3}}{8}\).
c) Gọi \(H\left( {a;b;c} \right)\)là hình chiếu vuông góc của \(B\)lên mặt phẳng \(\left( P \right)\). Khi đó \(a + b + c = 3\).
d) Gọi \(\Delta \)là đường thẳng vuông góc với mặt phẳng \(\left( P \right)\)sao cho khoảng cách từ \(A\)đến \(\Delta \)bằng \(\sqrt 2 \). Khi khoảng cách từ \(B\)đến \(\Delta \)đạt giá trị lớn nhất thì \(\Delta \)đi qua điểm \(M\left( {3;1; - 1} \right)\).
Trong không gian \[Oxyz\], một viên đạn được bắn ra từ vị trí \(A\left( {1;2;3} \right)\) hướng đến vị trí \(B\left( {0;1; - 6} \right)\), bia chắn là mặt phẳng \(\left( P \right):4x - y + 2z + 13 = 0\), đơn vị là kilomet.
a) Hình chiếu vuông góc của \(A\) trên \(\left( {Oxy} \right)\) là \(H\left( {0;2;3} \right)\).
b) Điểm \(B\) thuộc mặt phẳng \(\left( P \right)\).
c) Giả sử viên đạn chuyển động thẳng đều theo hướng vectơ \(\vec v = \left( { - 2; - 2; - 18} \right)\) với vận tốc 800 m/s (bỏ qua mọi lực cản và chướng ngại vật), sau một phút viên đạn bắn ra đi qua điểm \(B\).
d) Góc giữa đường thẳng \[AB\] và mặt phẳng \(\left( P \right)\) (làm tròn đến hàng đơn vị) là \(60^\circ \).
Một đài kiểm soát không lưu tại sân bay có nhiệm vụ kiểm soát, điều hành hoạt động bay của máy bay trong vòng bán kính \(70\,{\rm{km}}\). Để theo dõi hành trình của máy bay, ta có thể thiết lập hệ trục toạ độ \[Oxyz\] có gốc toạ độ \(O\) trùng với vị trí trung tâm của kiểm soát không lưu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (được coi là mặt phẳng) với trục \(Ox\) hướng về phía Tây, trục \(Oy\) hướng về phía Nam và trục \(Oz\) hướng thẳng đứng lên trời và đơn vị độ dài trên mỗi trục tọa độ là \(1\,{\rm{km}}\). Một máy bay trực thăng đang ở vị trí \(A\left( { - 65; - 25;30} \right)\) bay theo hướng Tây Nam với độ cao không đổi, vận tốc không đổi \(200\,{\rm{km/h}}\), quỹ đạo bay theo đường thẳng.
a) Khi máy bay ở vị trí \(A\) thì đài kiểm soát không lưu của sân bay theo dõi được máy bay.
b) Máy bay di chuyển theo hướng Tây Nam với quỹ đạo bay là đường thẳng \(d\) có phương trình: \(\left\{ \begin{array}{l}x = - 65 + t\\y = - 25 + t\\z = 30\end{array} \right.\).
c) Vùng kiểm không lưu của đài kiểm soát trên là vùng ở bên trong và trên bề mặt của mặt cầu \(\left( S \right)\) có phương trình: \({x^2} + {y^2} + {z^2} = 4900\).
d) Thời gian máy bay di chuyển trong phạm vi đài kiểm soát không lưu của sân bay theo dõi được là \(35\) phút.
Một đơn vị thiết kế theo đơn đặt hàng làm một nhà vườn ngoài trời để trồng rau. Người thiết kế đã vẽ mô hình nhà vườn trong hệ trục tọa độ \(Dxyz\) (đơn vị trên mỗi trục tính theo mét) như hình vẽ, với các cột nhà là các đoạn thẳng \(AE,\,BF,\,CG\) và \(DH\); phần mái là tứ giác \[EFGH\] và hình vuông \[ABCD\] nằm trên mặt đất. Biết độ dài các đoạn thẳng \[AB = 20\,{\rm{m}}\], \[DH = 4\,{\rm{m}}\], \[AE = BF = 3\,{\rm{m}}\].
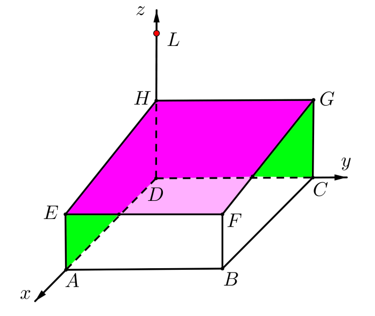
a)Tọa độ điểm\(B\left( {20;20;0} \right)\) và\(H\left( {0\,;0\,;4} \right)\).
b)Đường thẳng \(EH\) có phương trình tham số là \(\left\{ \begin{array}{l}x = 20t\\y = 0\\z = 4 + t\end{array} \right.,\,\left( {t \in \mathbb{R}} \right)\).
c) Mái nhà hợp với mặt đất một góc khoảng \(2,86^\circ \).
d) Khách hàng đặt một camera ở vị trí \(L\) trên cột \(DH\) và cách mặt đất \(8\,{\rm{m}}\). Một vật ở vị trí \(M\left( {a\,;b\,;c} \right)\) thỏa mãn \(MA = MB = MC = MD = 2\sqrt {66} \,{\rm{m}}\) thì cách camera \(10\sqrt 2 \,{\rm{m}}\).
Xét Trái Đất trong không gian Oxyz, với O là tâm Trái Đất, tia Ox chứa giao điểm của kinh tuyến gốc và xích đạo, tia Oz chứa điểm cực Bắc (N), tia Oy giao với xích đạo tại điểm thuộc bán cầu Đông, đơn vị trên mỗi trục tương ứng với bán kính Trái Đất là 6371 km. Ta nói một điểm P thuộc bán cầu Bắc có vĩ độ là \(\alpha ^\circ \)Bắc (ghi là \(\alpha ^\circ N\)) khi góc giữa đường thẳng OP và mặt phẳng chứa xích đạo bằng \(\alpha ^\circ \) (hình vẽ minh họa).
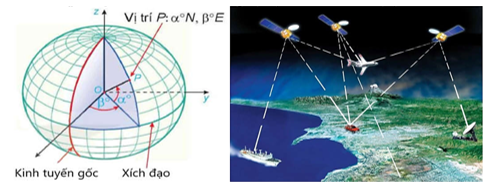
Hệ thống định vị toàn cầu GPS (Global Positioning System) cho phép xác định tọa độ một điểm bất kỳ trên mặt đất. GPS hoạt động bằng cách truyền tín hiệu từ mạng lưới vệ tinh quay quanh Trái Đất đến thiết bị thu GPS trên mặt đất. Trong cùng một thời điểm, thiết bị thu GPS cần xác định khoảng cách từ nó đến ít nhất ba vệ tinh để tính được tọa độ của nó.
Giả sử tại một thời điểm, một thiết bị thu GPS đặt tại M thuộc bán cầu Bắc trên mặt đất, thiết bị thu GPS này đo được khoảng cách đến các vệ tinh đang ở vị trí \[A\left( {3;1;2} \right),{\rm{ }}B\left( {3;2;1} \right),{\rm{ }}C\left( {3;6;4} \right)\] lần lượt là \(MA = \frac{{\sqrt {265} }}{5},MB = \sqrt {11} ,MC = \frac{{11\sqrt {10} }}{5}.\) Em hãy cho biết vĩ độ tại M là bao nhiêu độ Bắc (kết quả làm tròn đến hàng phần mười)?
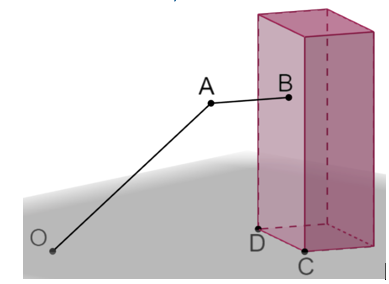
Một công ty logistics đang thử nghiệm hệ thống giao hàng tự động bằng máy bay không người lái (drone). Trong không gian \[Oxyz\], mỗi đơn vị trên các trục tương ứng với 1 mét trên thực tế, mặt ngoài của một tòa nhà cao tầng được xem là một phần của mặt phẳng \[\left( P \right)\] thẳng đứng, đi qua hai điểm \(C\left( {10;50;0} \right)\) và \(D\left( {30;10;0} \right)\) trên mặt đất (mặt phẳng \(\left( {Oxy} \right)\)) như hình vẽ. Vị trí giao hàng là điểm B nằm trên mặt phẳng \[\left( P \right)\]. Drone bắt đầu bay từ kho hàng tại gốc tọa độ \(O\left( {0;0;0} \right)\). Ban đầu, nó bay theo một đường thẳng đến vị trí \(A\left( {30;40;120} \right).\) Từ vị trí \[A\], drone thay đổi đường bay, di chuyển theo phương vuông góc với mặt phẳng \[\left( P \right)\] đến vị trí giao hàng \[B\]. Khoảng cách từ \(O\) đến \(B\) bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Một máy bay cất cánh tại một sân bay, sau khi bắt đầu cất cánh trong thời gian ngắn máy bay sẽ bay theo một đường thẳng và sân bay nơi máy bay cất cánh được coi là một mặt phẳng. Chọn hệ tọa độ \[Oxyz\], đơn vị độ dài trên mỗi trục là 1 km. Biết rằng, máy bay bắt đầu cất cánh tại điểm \[O\left( {0;0;0} \right)\]và sau một thời gian ngắn máy bay bay đến điểm \[A\left( {2;5;\,1,2} \right)\] và sân bay máy bay cất cánh nằm trên mặt phẳng \[\left( {Oxy} \right)\]. Góc tạo bởi đường bay của máy bay cất cánh và sân bay bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị theo đơn vị là độ)?
Khi gắn hệ tọa độ \[Oxyz\] (đơn vị trên mỗi trục tính theo kilômét) vào không gian, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu \[\left( S \right)\] (tập hợp những điểm nằm trên và nằm trong mặt cầu tương ứng). Biết rằng mặt cầu này có phương trình \[{x^2} + {y^2} + {z^2} - 4x - 6y - 2z + 5 = 0\]. Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là bao nhiêu kilômét?
Trong một trung tâm nghiên cứu robot bay, người ta bố trí một thiết bị định vị tại điểm cố định \(A\left( {1;0;2} \right)\) trong không gian ba chiều với hệ tọa độ \(Oxyz\) (các đơn vị tọa độ được tính bằng mét). Thiết bị này giao tiếp đồng thời với hai cảm biến: Cảm biến thứ nhất di chuyển dọc theo đường thẳng \(\Delta :\frac{{x - 3}}{1} = \frac{{y + 1}}{2} = \frac{{z - 4}}{{ - 1}}\), cảm biến thứ hai được gắn trên mặt phẳng \(\left( \alpha \right):2x - y + z + 1 = 0\). Giữa hai cảm biến được kết nối bằng một đường truyền BC, trong đó B nằm trên đường thẳng \(\Delta \), C nằm trên mặt phẳng \(\left( \alpha \right)\) và thiết bị định vị tại A là trung điểm của đoạn BC. Biết rằng đường thẳng BC có một vectơ chỉ phương \(\vec u = \left( { - 2;a;b} \right)\), hãy tính giá trị \(a + 2b\) (viết kết quả dưới dạng số thập phân).
Trạm tàu cứu hộ được đặt tại vị trí \(A\left( {5;\,0;\,0} \right)\) trên một hòn đảo nhỏ trong không gian \(Oxyz\) (đơn vị trên mỗi trục được tính bằng kilomet), được sử dụng làm trạm cứu hộ, cứu nạn trên biển. Tàu du lịch \(B\) đang di chuyển (vận tốc không đổi) trên tuyến đường được mô tả bởi đường thẳng \({d_1}:\,\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 2t\\z = 0\end{array} \right.\). Tàu chở hàng \(C\) đang di chuyển (vận tốc không đổi) trên tuyến đường vận tải được mô tả bởi đường thẳng \({d_2}:\,\left\{ \begin{array}{l}x = 2 - s\\y = 11 + s\\z = 0\end{array} \right.\). Do thời tiết xấu, nên hai tàu \(B\) và \(C\)gặp sự cố và cần được tiếp cận khẩn cấp. Trạm cứu hộ điều một tàu cứu hộ xuất phát từ \(A\) để lần lượt tiếp cận tàu du lịch \(B\) trước, sau đó đến tàu chở hàng \(C\). Xét vị trí tối ưu của tàu du lịch \(B\) dừng lại và tàu chở hàng\(C\)dừng lại saocho tổng quãng đường tàu cứu hộ cần đi \(T = AB + BC + CA\) là nhỏ nhất. Khi đó \({T_{\min }} = \sqrt a \,\,\,\left( {{\rm{km}}} \right)\), hãy tính \(a + 2026\).

