Đề ôn luyện Toán Chương 6. Vectơ và hệ trục tọa độ trong không gian (đề số 2)
22 câu hỏi
Cho hình hộp \(ABCD.A'B'C'D'\) có tâm O. Khi đó, \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} + \overrightarrow {AC'} \) bằng
\(\overrightarrow {BD} \).
\(2\overrightarrow {OC'} \).
\(4\overrightarrow {AO} \).
\(2\overrightarrow {AC} \)
Cho tứ diện ABCD. Gọi \(M,N\) lần lượt là trung điểm của \(AB,CD;G\) là trung điểm của MN. Chọn khẳng định sai trong các khẳng định sau.
\(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} \).
\(\overrightarrow {AD} + \overrightarrow {AC} = \overrightarrow {AN} \).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
\(\overrightarrow {GM} + \overrightarrow {GN} = \vec 0\).
Cho hình lập phương \(ABCD.EFGH\) cạnh bằng \(a\). Giá trị của \(\overrightarrow {AC} \cdot \overrightarrow {EG} \) bằng
\( - {a^2}\).
\({a^2}\).
\( - 2{a^2}\).
\(2{a^2}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) (tham khảo hình vẽ).
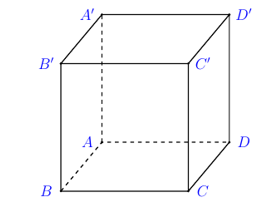
Góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD'} \) bằng
\(135^\circ \).
\(60^\circ \).
\(30^\circ \).
\(45^\circ \).
Trong không gian \(Oxyz\), cho \(\vec a = 2\overrightarrow i - 3\overrightarrow j + \vec k\). Tọa độ của \(\vec a\) là
\(\left( { - 2;1;3} \right)\).
\(\left( {2; - 3;1} \right)\).
\(\left( {2;1;3} \right)\).
\(\left( {2;1; - 3} \right)\).
Trong không gian Oxyz, cho các vectơ \(\vec a = \left( {1; - 1;2} \right),\vec b = \left( {2;1; - 3} \right),\vec c = \left( {0;3; - 2} \right)\). Điểm \(M\left( {x;y;z} \right)\) thỏa mãn \(\overrightarrow {OM} + \vec a = 2\vec b - \vec c\), tổng \(x + y + z\) bằng
3.
−3.
4.
−2.
Trong không gian Oxyz, cho hai vectơ \(\vec a = \left( {2;3;3} \right),\vec b = \left( {3;2; - 1} \right)\). Khi đó tích vô hướng \(\vec a \cdot \vec b\) bằng:
\(\vec a \cdot \vec b = 9\).
\(\vec a \cdot \vec b = 7\).
\(\vec a \cdot \vec b = 3\).
\(\vec a \cdot \vec b = 15\).
Trong không gian Oxyz, cho 2 điểm \(A\left( {1; - 2; - 3} \right)\) và \(B\left( {7; - 14;11} \right)\). Tọa độ trung điểm của đoạn thẳng AB là:
\(\left( {4; - 6;4} \right)\).
\(\left( {4; - 8;4} \right)\).
\(\left( { - 4;6; - 4} \right)\).
\(\left( { - 4;8; - 4} \right)\).
Trong không gian tọa độ Oxyz, cho điểm \(M\left( {1; - \sqrt 2 ;\sqrt 3 } \right)\). Tìm điểm \(M' \in Ox\) sao cho độ dài đoạn thẳng \(MM'\) ngắn nhất.
\(M'\left( { - 1;0;0} \right)\).
\(M'\left( {1;0;0} \right)\).
\(M'\left( {1;0;\sqrt 3 } \right)\).
\(M'\left( {1; - \sqrt 2 ;0} \right)\).
Trong không gian Oxyz, cho hai điểm \(A\left( {0;2;1} \right)\) và \(B\left( {3; - 2;1} \right)\). Độ dài đoạn thẳng AB bằng
25.
5.
3.
9.
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1; - 2;3} \right);B\left( {2; - 3;4} \right)\).Tìm điểm \(M \in \left( {Oxy} \right)\) sao cho ba điểm \(A,B,M\) thẳng hàng.
\(M\left( {1;1;0} \right)\).
\(M\left( {3; - 4;5} \right)\).
\(M\left( { - 3;5;0} \right)\).
\(M\left( { - 2;1;0} \right)\).
Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm \(M\left( {2\,;\, - 2\,;\,1} \right)\) trên mặt phẳng \(\left( {Oxy} \right)\) có tọa độ là
\(\left( {2\,;\,0\,;\,1} \right)\).
\(\left( {0\,;\, - 2\,;\,1} \right)\).
\(\left( {2\,;\, - 2\,;\,0} \right)\).
\(\left( {0\,;\,0\,;\,1} \right)\).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;0; - 2} \right),B\left( { - 2;3;4} \right),C\left( {4; - 6;1} \right)\).
a) \(\overrightarrow {AB} = \left( {3; - 3;6} \right)\).
b) Hình chiếu vuông góc của \(B\) lên trục \(Ox\) là \(B'\left( { - 2;3;0} \right)\).
c) Tồn tại 1 điểm \(M\) thuộc trục hoành sao cho tam giác \(MBC\) vuông tại \(M\).
d) Nếu \(ABDC\) là hình bình hành thì tọa độ điểm \(D\) là \(\left( {1; - 3;7} \right)\).
Một phòng học có thiết kế dạng hình hộp chữ nhật \(ABCD.A'B'C'D'\) với \[AB = 6{\rm{\;m}}\]; \[AD = 7{\rm{\;m}}\];\(AA' = 3,5{\rm{\;m}}\). Một bóng đèn được treo ở vị trí chính giữa trần nhà của phòng học và cách trần nhà \(0,5{\rm{\;m}}\). Chọn hệ trục tọa độ Oxyz sao cho gốc \(O\) trùng với điểm \(A\), các điểm \(B,D,A'\) lần lượt nằm trên các tia \(Ox,Oy,Oz\).
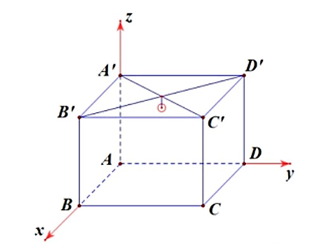
a) Điểm \(D\) có toạ độ là \(\left( {0;7;0} \right)\).
b) Các điểm \(C,D\)có tung độ bằng nhau.
c) Vectơ \(\overrightarrow {C'D'} \) có tọa độ \(\left( {6;0;0} \right)\).
d) Bóng đèn nằm tại vị trí có tọa độ \(\left( {3;3,5;3,5} \right)\).
Một chiếc đĩa kim loại khối lượng 4,6 kg được treo bởi ba sợi dây \(SA,\,\,SB,\,\,SC\) sao cho \(S.ABC\) làhình chóp đều có \(\widehat {ASB} = 60^\circ \) (tham khảo hình vẽ). Khối lượng dây không đáng kể, lực căng của mỗi sợi dây \(SA,\,\,SB,\,\,SC\) đặt tại điểm \(S\) tương ứng là \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) có độ lớn bằng nhau. Lấy độ lớn của gia tốc trọng trường \(\left| {\vec g} \right| = 9,8\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\).
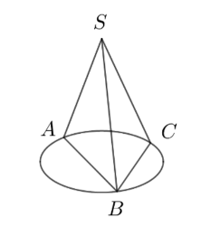
a) \(\overrightarrow {SA} ,\,\,\overrightarrow {SB} ,\,\,\overrightarrow {SC} \) là ba vectơ đồng phẳng.
b) \(\overrightarrow {{F_1}} \cdot \overrightarrow {{F_2}} = \left| {\overrightarrow {{F_1}} } \right| \cdot \left| {{{\vec F}_2}} \right| \cdot {\rm{cos}}\left( {{{\vec F}_1},\overrightarrow {{F_2}} } \right)\).
c) Trọng lực \(\vec P\) của hệ vật có độ lớn bằng \(41,08\,{\rm{N}}\).
d) Độ lớn của các lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) bằng \(19,04\,{\rm{N}}\).
Một tháp trung tâm kiểm soát không lưu ở sân bay cao \[100\]m sử dụng radar có phạm vi theo dõi \[600\]km được đặt trên đỉnh tháp. Chọn hệ trục toạ độ \[Oxyz\]có gốc \[O\] trùng với vị trí chân tháp, mặt phẳng \[\left( {Oxy} \right)\] trùng với mặt đất sao cho trục \[Ox\] hướng về phía tây, trục \[Oy\] hướng về phía nam, trục \[Oz\] hướng thẳng đứng lên phía trên (đơn vị độ dài trên mỗi trục là kilômét).

Một máy bay tại vị trí \[F\] cách mặt đất \[12\] km, cách \[400\] km về phía tây và \[300\] km về phía bắc so với tháp trung tâm kiểm soát không lưu. Từ vị trí \(F\), máy bay bay với tốc độ \(900\,{\rm{km/h}}\), theo hướng của vectơ \(\overrightarrow a = \left( {3;4;0} \right)\) sau một giờ đến vị trí \(A\).
a)Tọa độ của radar đặt trên tháp là \[\left( {0;0;0,1} \right)\].
b) Vị trí \(F\)nằm trong phạm vi kiểm soát của radar.
c) Vị trí \(A\)có tọa độ \(A\left( {940;420;0} \right)\).
d) Trong khoảng thời gian một giờ máy bay bay từ vị trí \(F\)đến vị trí \(A\), máy bay có không quá \(21\) phút bay trong phạm vi theo dõi của của radar.
Trong không gian \(Oxyz\)(đơn vị lấy theo km), radar phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm \(A\left( {800;\,500;\,7} \right)\) đến điểm \(B\left( {940;\,550;\,8} \right)\)trong \(10\)phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau \(10\)phút tiếp theo là \(D\left( {x;\,y;\,z} \right)\). Khi đó, \(x - y + z\) bằng bao nhiêu?
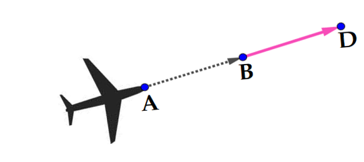
Cơn bão Yagi gây thiệt hại nghiêm trọng về người và tài sản cho nước ta, trong đó nặng nề nhất là tại thôn Làng Nủ, xã Phúc Khánh, huyện Bảo Yên, tỉnh Lào Cai, lũ quét và sạt lở đất đã vùi lấp 40 ngôi nhà. Cả nước đã chung tay ủng hộ và xây dựng lại nhà sàn cho người dân Làng Nủ theo thiết kế như hình vẽ dưới đây.
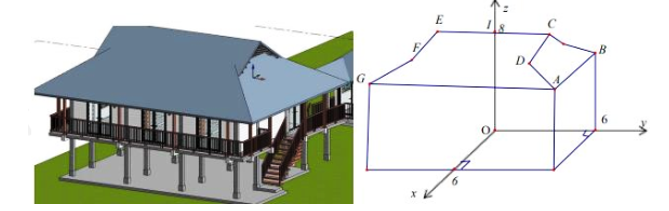
Giả sử áp dụng hệ trục tọa độ \(Oxyz\) như hình vẽ (đơn vị trên các trục là mét). Xét một bên của mái nhà gồm một hình chữ nhật CDFE và một hình thang cân ADFG với các điểm \(G\left( {6; - 6;6} \right)\), \(C\left( {3;4;8} \right),F\left( {4; - 4;7} \right)\) và điểm \(I\) là trung điểm CE.Biết góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {AB} \) bằng \(a^\circ \). Tìm a.
Hai chiếc máy bay không người lái cùng bay lên từ một địa điểm. Sau một giờ bay, chiếc thứ nhất cách điểm xuất phát về phía bắc 23 km và về phía tây 18 km, đồng thời cách mặt đất 2 km. Chiếc thứ hai cách điểm xuất phát về phía nam 22 km và về phía đông 27 km, đồng thời cách mặt đất 3 km. Chọn hệ trục tọa độ Oxyz với gốc O đặt tại điểm xuất phát của hai chiếc máy bay, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất sao cho trục Ox hướng về phía bắc, trục Oy hướng về phía tây và trục Oz hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét. Sau đúng một giờ bay, hai máy bay đó cùng bắn một mục tiêu di động trên mặt đất. Biết tổng khoảng cách từ mỗi máy bay đến mục tiêu là nhỏ nhất, lúc đó mục tiêu cách điểm xuất phát của hai máy bay bao nhiêu kilômét (kết quả làm tròn đến hàng phần trăm)?
Bên trong một căn nhà bỏ hoang hình lập phương cạnh \(5\,\,{\rm{m}}\) có 3 chú nhện sinh sống. Mùa đông đến, vì đói rét nên chúng đành quyết định hợp tác với nhau giăng lưới để bắt mồi. Ba chú nhện tính toán sẽ giăng một mảnh lưới hình tam giác theo cách sau: Mỗi chú nhện sẽ đứng ở mép tường bất kì (có thể mép giữa 2 bức tường, giữa tường với trần, hoặc giữa tường với nền) rồi phóng những sợi tơ làm khung đến vị trí của 2 con nhện còn lại rồi sau đó mới phóng tơ dính đan phần lưới bên trong. Chúng quy định không có bất kì 2 con nhện nào cùng nằm trên một mặt tường, nền hoặc trần nhà. Chu vi nhỏ nhất của mảnh lưới được giăng (biết các sợi tơ khung căng và không nhùn) là \[\frac{m}{p}\sqrt n \] với \(m,\,n,\,p \in {\mathbb{N}^*};\,\,\frac{m}{p}\) là phân số tối giản. Tính giá trị của biểu thức \({m^2} + {n^2} + {p^2}\)
Khi khắc phục hậu quả của thiên tai, bão lũ, một trong những giải pháp nhằm tiếp tế hàng cứu trợ đến những nơi khó tiếp cận là sử dụng flycam để xác định vị trí chính xác của người cần cứu trợ, sau đó sử dụng drone để vận chuyển các vật dụng thiết yếu thả xuống cho người này, giúp họ có thể cầm cự trong khi chờ đợi lực lượng cứu hộ đến nơi. Hai chiếc drone làm nhiệm vụ chuyển hàng cứu trợ bay lên từ cùng một địa điểm. Chiếc thứ nhất bay đến điểm cách điểm xuất phát \(2,5\,\,{\rm{km}}\) về phía nam và \(1,5\,\,{\rm{km}}\) về phía đông, đồng thời cách mặt đất \(60\,\,{\rm{m}}{\rm{.}}\) Chiếc thứ hai bay đến điểm cách điểm xuất phát \(3\,\,{\rm{km}}\) về phía bắc và \(2,5\,\,{\rm{km}}\) về phía tây, đồng thời cách mặt đất \(40\,\,{\rm{m}}.\)Trong không gian, xét hệ tọa độ \(Oxyz\) với gốc toạ độ \(O\) đặt tại điểm xuất phát của hai drone, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (được coi là mặt phẳng). Giả sử trong trường hợp khẩn cấp, cần tìm một vị trí trên mặt đất để tiếp nhiên liệu và các vật dụng cứu trợ cho hai drone sao cho tổng khoảng cách từ vị trí tiếp nhiên liệu đó tới hai drone nhỏ nhất. Vị trí cần tìm cách gốc tọa độ \(a\,\,{\rm{km}}\) theo hướng bắc và \(b\,\,{\rm{km}}\) theo hướng tây. Khi đó \(a + b\) bằng bao nhiêu?

Một giỏ hoa treo trong nhà làm bằng \(3\) sợi dây không giãn, mỗi sợi dài \(60\,{\rm{cm}}\), miếng kê là một miếng gỗ cân đối hình tròn bán kính \(20\,{\rm{cm}}\), ba sợi dây được thắt một đầu bên trên và đỡ giá gỗ tại 3 điểm tạo thành tam giác đều (giả sử mối thắt của 3 sợi dây và mối nối của mỗi sợi dây với miếng gỗ không đáng kể). Biết lực chịu đựng của mỗi sợi dây bằng nhau và mỗi sợi chịu không quá \(15\,{\rm{N}}\), trọng lượng của miếng giá gỗ là \(5\,{\rm{N}}\). Tính trọng lượng tối đa của các chậu hoa để dây treo không bị đứt (đơn vị Newton, kết quả làm tròn đến hàng phần chục).


