Đề ôn luyện Toán Chương 6. Vectơ và hệ trục tọa độ trong không gian (đề số 1)
22 câu hỏi
Cho hình lập phương\(ABCD.A'B'C'D'\) cạnh \(a\). Khẳng định nào sau đây là sai?
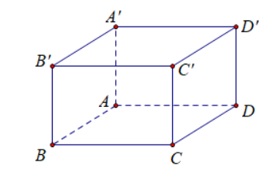
\[\left| {\overrightarrow {BD} } \right| = a\sqrt 2 \].
\[\left| {\overrightarrow {BD'} } \right| = a\sqrt 3 \].
\[\overrightarrow {AC} + \overrightarrow {A'C'} = \vec 0\].
\[\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\).
Tổng \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} \) bằng
\(4\overrightarrow {SO} \).
\(8\overrightarrow {SO} \).
\(3\overrightarrow {SO} \).
\(2\overrightarrow {SO} \).
Cho tứ diện ABCD, gọi \(G\) là trọng tâm của tam giác BCD. Phát biểu nào sau đây là đúng?
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
\(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {DA} \).
\(\overrightarrow {AB} + \overrightarrow {DC} - \overrightarrow {DB} = \overrightarrow {CA} \).
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
Cho tứ diện đều ABCD có cạnh \(a\). Tích vô hướng \(\overrightarrow {BA} \cdot \overrightarrow {BC} \) bằng
\( - \frac{{{a^2}\sqrt 3 }}{2}\).
\( - \frac{{{a^2}}}{2}\).
\(\frac{{{a^2}}}{2}\).
\(\frac{{{a^2}\sqrt 3 }}{2}\).
Trong không gian \(Oxyz\), cho các vectơ \(\vec u = \vec i + 2\vec j - 3\vec k,\vec v = 2\vec i - \vec j + \vec k,\vec w = \vec u + \vec v\). Toạ độ của vectơ \(\vec w\) là
\(\vec w = \left( {3; - 1;2} \right)\).
\(\vec w = \left( {3;1; - 2} \right)\).
\(\vec w = \left( {3;1;2} \right)\).
\(\vec w = \left( {3; - 1; - 2} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {2; - 1; - 1} \right),B\left( { - 3;2; - 2} \right)\). Tọa độ của \(\overrightarrow {AB} \) là
\(\left( {5; - 3; - 1} \right)\).
\(\left( {5; - 3;1} \right)\).
\(\left( { - 5;1; - 1} \right)\).
\(\left( { - 5;3; - 1} \right)\).
Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;3;4} \right),B\left( {2; - 1;0} \right),C\left( {3;1;2} \right)\). Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là
\(G\left( {3;\frac{2}{3};3} \right)\).
\(G\left( {2; - 1;2} \right)\).
\(G\left( {2;1;2} \right)\).
\(G\left( {6;3;6} \right)\).
Trong không gian Oxyz, cho điểm \(M\) thoả mãn \(\overrightarrow {OM} = 2\vec i + 3\vec j - 4\vec k\). Tìm tọa độ điểm \(H\) là hình chiếu vuông góc của điểm \(M\) lên mặt phẳng \(\left( {Oyz} \right)\).
\(H\left( {2;0;0} \right)\).
\(H\left( {0;3; - 4} \right)\).
\(H\left( {2;3; - 4} \right)\).
\(H\left( { - 2; - 3;4} \right)\).
Trong không gian Oxyz, cho \(\vec a = \left( {2; - 3;3} \right),\vec b = \left( {0;2; - 1} \right),\vec c = \left( {3; - 1;5} \right)\). Tọa độ của vectơ \(\vec u = 2\vec a + 3\vec b - 2\vec c\) là
\(\left( {10; - 2;13} \right)\).
\(\left( { - 2;2; - 7} \right)\).
\(\left( { - 2; - 2;7} \right)\).
\(\left( { - 2;2;7} \right)\).
Trong không gian \(Oxyz\), cho các điểm \(A\left( {1;3;2} \right)\), \(B\left( {1;0;1} \right)\), \(C\left( {5; - 3;2} \right)\). Biết rằng \(\overrightarrow {AB} \cdot \overrightarrow {AC} = 2m\). Giá trị của \(m\) là
\(m = - 9\).
\(m = 9\).
\(m = 18\).
\(m = - 18\).
Trong không gian Oxyz, cho hai vector \(\vec u = \left( { - 1;1;0} \right),\vec v = \left( {0; - 1;0} \right)\). Góc giữa hai vectơ đã cho bằng
\(120^\circ \).
\(60^\circ \).
\(135^\circ \).
\(45^\circ \).
Trong không gian Oxyz, cho \(\vec a = \left( {2; - 2;6} \right)\). Khi đó độ dài của vectơ \(\vec a\) là:
\(\left| {\vec a} \right| = 6\).
\(\left| {\vec a} \right| = 2\sqrt {11} \).
\(\left| {\vec a} \right| = 44\).
\(\left| {\vec a} \right| = \sqrt {11} \).
Trong không gian\[Oxyz\], cho các điểm \[A\left( {5;3;4} \right),B\left( {1;2;1} \right),C\left( {8; - 3;2} \right)\]. Gọi \[D\left( {a;b;c} \right)\] là chân đường phân giác trong kẻ từ đỉnh \[A\]của tam giác \[ABC\].
a) Trọng tâm của tam giác \[ABC\] là \[G\left( {\frac{{14}}{3};\frac{2}{3};\frac{7}{3}} \right)\].
b)\[BC = 5\sqrt 2 \].
c) Tam giác \[ABC\]là tam giác vuông.
d) Giá trị \[a + 2b + 3c\] là một số nguyên.
Trong không gian \(Oxyz\) (đơn vị trên mỗi trục là 1 m), một flycam bay với vận tốc có độ lớn và hướng không đổi. Tại thời điểm \(t = 0\), flycam ở vị trí \(A\left( {1;\,2;\,3} \right)\) và sau 10 phút nó ở vị trí \(B\left( {21;\,32;\,33} \right)\).
a)Flycam không bay qua vị trí \[D\left( {5;\,8;\,9} \right)\].
b)Vectơ vận tốc của flycam có tọa độ là \(\overrightarrow v = \left( {20;\,30;\,30} \right)\).
c)Độ lớn của vận tốc flycam là \(\sqrt {22} \) (m/phút).
d)Sau 15 phút vị trí flycam là \(C\left( {31;\,47;\,48} \right)\).
Nhà bác An được mô tả như hình vẽ bên dưới, trong đó phần thân nhà là hình hộp chữ nhật \(ABCD.EFGH\). Ngôi nhà được lợp ngói hai mái là hai hình chữ nhật \(PEHQ\) và \(PFGQ\), biết tam giác \(EFP\) là tam giác cân tại \(P\). Gọi \(T\) là trung điểm của cạnh \(DC\). Các kích thước của nhà lần lượt là \(AB = 6\,{\rm{m}}\), \(AE = 5\,{\rm{m}}\), \(AD = 8\,{\rm{m}}\), \(QT = 7\,{\rm{m}}\). Xét hệ trục tọa độ \(Oxyz\) sao cho gốc tọa độ là điểm \(O\) thuộc đoạn \(AD\) sao cho \(OA = 2\,{\rm{m}}\) và các trục tọa độ tương ứng là các trục \(Ox,Oy,Oz\).
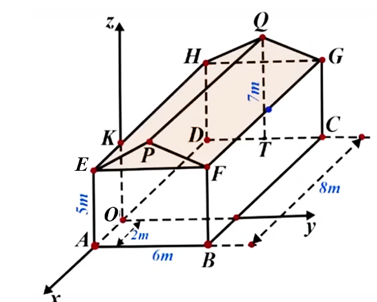
a) Toạ độ điểm \(A\) là \(\left( {2;0;0} \right)\).
b) Vectơ \(\overrightarrow {AC} \) có toạ độ là \(\left( {6;6;0} \right)\).
c) Mái nhà bác An được lợp bằng ngói đất nung Đất Việt, giá tiền mỗi viên ngói là \(11000\) đồng và để lợp được \(1\)\({{\rm{m}}^{\rm{2}}}\) diện tích mái cần \(22\) viên ngói. Số tiền cần bỏ ra để mua ngói lợp mái nhà là \(13\,960\,000\) đồng (không kể hao phí do việc cắt và ghép các viên ngói, làm tròn kết quả đến hàng nghìn).
d) Bác An muốn lắp một chiếc đèn lồng tại vị trí trung điểm của \(FG\) và đầu nguồn điện đặt tại vị trí \(O\). Bác ấy thiết kế đường dây điện nối từ \(O\) đến \(K\) sau đó nối đến chiếc đèn lồng. Độ dài đoạn dây điện nối tối thiểu bằng \(5 + 2\sqrt {10} \,\,{\rm{(m)}}\).
Trong không gian, xét hệ tọa độ \(Oxyz\) có gốc \(O\) trùng với vị trí một giàn khoan trên biển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt biển (được coi là mặt phẳng) với tia \(Ox\) hướng về phía nam, tia \(Oy\) hướng về phía đông và tia \(Oz\) hướng thẳng đứng lên trời (tham khảo hình vẽ). Đơn vị đo trong không gian \(Oxyz\) lấy theo kilômét. Một chiếc radar đặt tại \(O\) có phạm vi theo dõi là 30 km. Một chiếc tàu thám hiểm tại vị trí \(A\) ở độ sâu 10 km so với mặt nước biển, cách \(O\;25\;{\rm{km}}\) về phía nam và 15 km về phía tây. Một tàu đánh cá tại vị trí \(B\left( { - 20;15;0} \right)\).

a) Khoảng cách từ chiếc tàu thám hiểm đến radar bằng 25 km.
b) Radar không phát hiện được tàu thám hiểm đặt tại vị trí \(A\).
c) Radar phát hiện ra tàu đánh cá tại vị trí \(B\).
d) Một chiếc tàu của cảnh sát biển đang tuần tra di chuyển đến vị trí cách \(O\)\(\;15\;{\rm{km}}\) về phía nam.
Để radar phát hiện ra thì tàu cảnh sát biển cần di chuyển về phía đông cách \(O\) tối đa \(15\sqrt 3 \;{\rm{km}}\).
Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân. Trọng lực tác dụng lên chiếc máy có độ lớn là \(30\,{\rm{N}}\) và được phân bố thành ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) lên ba chân của giá đỡ. Ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) có độ lớn bằng nhau và góc tạo bởi mỗi chân của giá đỡ và mặt đất là \(60^\circ \). Hỏi độ lớn của lực \(\overrightarrow {{F_1}} \) là bao nhiêu Newton (làm tròn đến hàng phần chục)?

Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), radar phát hiện một chiếc máy bay di chuyển với tốc độ và hướng không đổi từ điểm \(A\left( {800;500;7} \right)\) đến điểm \(B\left( {940;550;9} \right)\) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là \(C\left( {x;y;z} \right)\). Tính \(x + y + z\).
Một ngôi nhà gồm hai phần. Phần thân nhà dạng hình hộp chữ nhật \[ABCD.OMNK\]có chiều dài 1200 cm, chiều rộng 900 cm, chiều cao 450 cm. Phần mái nhà dạng hình chóp S.ABCD có các cạnh bên bằng nhau và cùng tạo với mặt đáy một góc a có \(\tan \alpha = \frac{1}{5}\). Chọn hệ trục toạ độ Oxyz sao cho M thuộc tia Ox, K thuộc tia Oy, A thuộc tia Oz (như hình vẽ).
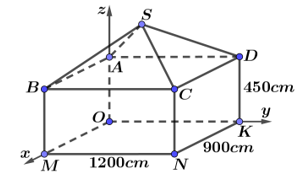
Biết \[S\left( {a;b;c} \right)\] (đơn vị của a, b, c là centimet). Tính giá trị của biểu thức \[P = a + b + c\].
Một chiếc máy bay không người lái bay lên tại một điểm. Sau một thời gian bay, chiếc máy bay cách điểm xuất phát về phía Bắc 55 km và về phía Tây 20 km, đồng thời cách mặt đất 1,5 km. Khi đó, khoảng cách của chiếc máy bay với vị trí tại điểm xuất phát bằng bao nhiêu kilômét? (kết quả làm tròn đến một chữ số thập phân).
Trong không gian \[Oxyz\], cho các điểm \(A\left( { - 1; 2; 1} \right)\),\(B\left( {2; - 1; 3} \right)\),\[C\left( {3; 5; - 1} \right)\]. Điểm \[M\left( {a; b; c} \right)\] trên mặt phẳng \(\left( {Oyz} \right)\) sao cho \(\left| {\overrightarrow {MA} + 2\overrightarrow {MB} - \overrightarrow {CM} } \right|\) đạt giá trị nhỏ nhất. Khi đó ta có \(2b + c\) bằng bao nhiêu?
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Sau một thời gian chiếc thứ nhất cách điểm xuất phát 300 m về phía Nam và 100 m về phía Đông, đồng thời cách mặt đất 100 m. Chiếc thứ hai nằm cách điểm xuất phát 200 m về phía Bắc và 100 m về phía Tây, đồng thời cách mặt đất 50 m. Cùng thời điểm đó, một người đứng trên mặt đất quan sát thấy hai chiếc khinh khí cầu nói trên. Biết rằng, so với các vị trí quan sát trên mặt đất, vị trí người đứng có tổng khoảng cách đến hai chiếc khinh khí cầu là nhỏ nhất. Tính khoảng cách từ vị trí người quan sát đến địa điểm xuất phát của hai chiếc khinh khí cầu (kết quả làm tròn đến hàng đơn vị của mét).

