Đề ôn luyện Toán Chương 5. Hình học không gian (đề số 2)
22 câu hỏi
Cho hình hộp chữ nhật \(ABCD.A\prime B\prime C\prime D\prime \) có \(AB = a,{\rm{ }}AD = \sqrt 3 a,{\rm{ }}AA\prime = 2\sqrt 3 a\) (tham khảo hình vẽ).
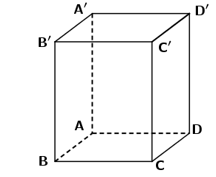
Khoảng cách giữa hai mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {A'B'C'D'} \right)\) bằng
\(a\).
\(2a\sqrt 3 \).
\(3a\).
\(a\sqrt 3 \).
Cho hình chóp \({\rm{S}}.ABCD\) có đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(SO \bot \left( {ABCD} \right)\). Gọi \(H,\,K\) lần lượt là trung điểm của \(BC,\,AD\). Khẳng định nào sau đây đúng?
\(BC \bot \left( {SAB} \right)\).
\(BC \bot \left( {SHK} \right)\).
\(HK \bot \left( {SCD} \right)\).
\(HK \bot \left( {SBD} \right)\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B.\) Cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Biết \(SA = AB = 2a\), \(BC = 3a\). Tính thể tích của \(S.ABC\) là
\[3{a^3}\].
\[4{a^3}\].
\[2{a^3}\].
\[{a^3}\].
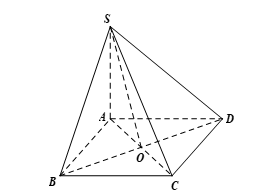
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) cạnh là \[a\], \(SA\) vuông góc với đáy \(ABCD\) và \[SB = 2a\]. Khoảng cách từ điểm \(S\) đến đường thẳng\(AB\) bằng
\(a\sqrt 2 \).
\(a\sqrt 3 \).
\(a\).
\(2a\).
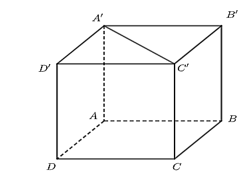
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(AB\) và \(A'C'\) bằng
\(30^\circ \).
\(90^\circ \).
\(60^\circ \).
\(45^\circ \).
Cho hình lăng trụ đứng \[ABC.A'B'C'\] có đáy \[ABC\] là tam giác vuông tại\[A\]. Góc giữa đường thẳng \[AB\] và mặt phẳng \[\left( {ACC'A'} \right)\] bằng
\[60^\circ \].
\[90^\circ \].
\[45^\circ \].
\[30^\circ \].
Cho hình chóp cụt đều có diện tích hai đáy lần lượt bằng \(4\sqrt 3 \)và\(\sqrt 3 \),chiều cao bằng 4. Thể tích khối chóp cụt đều đã cho bằng
\(V = \frac{{28\sqrt 3 }}{3}\).
\(V = \frac{{24\sqrt 3 }}{3}\).
\(V = \frac{{28\sqrt 3 }}{9}\).
\(V = 28\sqrt 3 \).
Khối chóp \(S.ABC\) có diện tích đáy \(ABC\) bằng 5. Thể tích khối chóp \(S.ABC\) bằng 15. Khoảng cách từ \[S\] đến mặt phẳng \[\left( {ABC} \right)\] là
60.
16.
4.
9
Cho hình chóp \(S.ABCD\) có \(SB \bot \left( {ABCD} \right)\), đáy \[ABCD\] là hình thoi. Một góc phẳng nhị diện của góc nhị diện \[\left[ {A,SB,C} \right]\] là
\(\widehat {ABC}\).
\(\widehat {BAD}\).
\(\widehat {ACD}\).
\(\widehat {SAC}\)
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) vuông tại\[C\].Kết luận nào sau đây là sai?
\(\left( {SAB} \right) \bot \left( {SBC} \right)\).
\(\left( {SAC} \right) \bot \left( {ABC} \right)\).
\(\left( {SAB} \right) \bot \left( {ABC} \right)\).
\(\left( {SAC} \right) \bot \left( {SBC} \right)\).
Cho khối lăng trụ có diện tích đáy bằng 2 và thể tích bằng 8. Chiều cao của khối lăng trụ đã cho là
12.
16.
4.
\(\frac{1}{4}\).
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a\). Khoảng cách giữa hai đường thẳng \(AC'\) và \(BB'\) bằng
\(\frac{a}{2}\).
\(a\).
\(\frac{{a\sqrt 3 }}{4}\).
\(\frac{{a\sqrt 3 }}{2}\).
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng 4cm, chiều cao bằng 2 cm.
a)\(d\left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = 2\,{\rm{cm}}\).
b) Trong mặt phẳng \(\left( {A'B'C'} \right)\), kẻ \(C'H \bot A'B'\) tại \(H\). Khi đó \(AB \bot \left( {CC'H} \right)\).
c) Khoảng cách từ điểm \(C'\) đến mặt phẳng \(\left( {ABB'A'} \right)\) bằng \(\sqrt 3 \,{\rm{cm}}\).
d) Thể tích khối lăng trụ là \(8\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\)
Cho hình chóp \(S.ABC\) có mặt bên \(\left( {SAB} \right)\) vuông góc với mặt đáy và tam giác \[SAB\] đều cạnh \(2a\). Biết tam giác \(ABC\) vuông tại \(C\) và cạnh \(AC = a\sqrt 3 \). Gọi \(H\) là trung điểm của \(AB\).
a) \(SH \bot \left( {ABC} \right)\).
b) Mặt phẳng \(\left( {SHC} \right)\) và \(\left( {ABC} \right)\) vuông góc với nhau.
c) Thể tích của khối chóp \(S.ABC\) bằng \(\frac{{{a^3}}}{6}\).
d) \(d\left( {C,\left( {SAB} \right)} \right) = \frac{{a\sqrt 3 }}{3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a.\) Cạnh bên \(SA\)vuông góc với mặt đáy và \(SA = 2a\) (tham khảo hình vẽ).
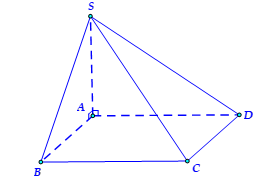
a) Thể tích khối chóp \(S.ABCD\) là \[{V_{S.ABCD}} = \frac{{2{a^3}}}{3}.\]
b) \[BD \bot \left( {SAC} \right).\]
c) Gọi \(\alpha \) là góc giữa \(SB\) và mặt phẳng \(\left( {ABCD} \right)\). Khi đó \(\tan \alpha = 2.\)
d) Số đo góc nhị diện \(\left[ {A,SD,C} \right]\) bằng \(90^\circ \).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\)là hình vuông và \(SA \bot \left( {ABCD} \right)\). Biết \(SA = 2a\), \(AB = a\).
a)\(AC \bot \left( {SBD} \right)\).
b) Gọi \(H\) hình chiếu của \(A\) lên \(SB\). Ta có \(AH \bot SC\).
c)\(d\left( {A,\left( {SBD} \right)} \right) = \frac{{2\sqrt 3 a}}{3}\).
d) Thể tích của khối chóp là \(V = \frac{{2{a^3}}}{3}\)
Bạn An muốn làm các viên đá có dạng khối chóp cụt tứ giác đều có cạnh của đáy lớn bằng \(3\,{\rm{cm}}\), cạnh của đáy nhỏ bằng \(1,5\,{\rm{cm}}\)và cao \(3\,{\rm{cm}}\) bằng cách dùng khay đá, mỗi khay sẽ tạo được \(6\) viên đá. Hỏi bạn An cần ít nhất bao nhiêu khay để chứa đồng thời \(2\) lít nước?

Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(4\sqrt 3 \). Số đo góc nhị diện \(\left[ {A,BC,S} \right]\) bằng \(30^\circ \). Tính thể tích khối chóp \(S.ABCD\).
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh bằng \(15\). Gọi \(M,\)\(N\) lần lượt là trung điểm của \(AC\) và \(B'C'.\) Tính khoảng cách giữa hai đường thẳng \(MN\) và \(B'D'\).
Cho hình chóp tứ giác đều \(S.ABCD\), có \(O\)là giao điểm của \(AC\) và \(BD\). Biết \[SO = AB = 2\]. Giá trị sin của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBC} \right)\) bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm).
Anh Bình có một căn phòng có dạng hình hộp chữ nhật có kích thước \(4{\rm{m}}\,\, \times \,\,6{\rm{m}}\). Anh muốn trang trí cho căn phòng của mình bằng các sợi đèn led bằng cách cố định một đầu vào chính giữa trần nhà, đầu còn lại anh gắn vào các mặt xung quanh của căn phòng. Tính độ dài ngắn nhất của sợi dây mà anh Bình có thể dùng để trang trí cho căn phòng của mình (đơn vị: mét).
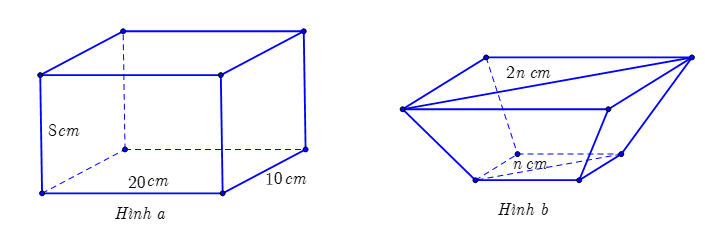
Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với các kích thước: chiều dài \(20\) cm, chiều rộng \(10\) cm, chiều cao \(8\) cm (Hình a). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài \(n\,\,\left( {{\rm{cm}}} \right)\), miệng khay là hình vuông lớn có đường chéo dài \(2n\left( {{\rm{cm}}} \right)\) (Hình b). Sau khi đổ, mực nước ở khay thứ hai cao bằng \(\frac{2}{5}\) chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi \(\frac{1}{4}\) so với ban đầu. Thể tích của chiếc khay thứ hai theo đơn vị centimét khối có kết quả chính xác đến hàng đơn vị là \(a\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\), hỏi tổng các chữ số của số \(a\) bằng bao nhiêu?