Đề ôn luyện Toán Chương 5. Hình học không gian (đề số 1)
22 câu hỏi
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Biết \(SA = 2a\) và \[SA\] vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABCD} \right)\) bằng
\(a\).
\(2a\).
\(3a\).
\(a\sqrt 2 \).
Cho khối lăng trụ có diện tích đáy \(3{a^2}\) và chiều cao \(2a\). Thể tích khối lăng trụ đã cho bằng
\({\rm{3}}{a^3}\)
\({a^3}\).
\(6{a^3}\).
\({\rm{2}}{a^3}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\) (tham khảo hình vẽ).
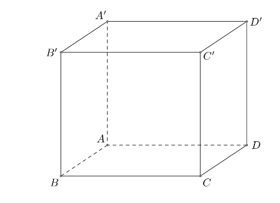
Khoảng cách giữa đường thẳng \(BD\)và mặt phẳng \(\left( {A'B'C'D'} \right)\) bằng
\(a\).
\(a\sqrt 3 \).
\(3a\).
\(a\sqrt 2 \).
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Biết \(AB = 9a\), \(AD = 10a\). Khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAD} \right)\) là
\(\sqrt {19} a\).
\(\sqrt {181} a\).
\(10a\).
\(9a\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) vuông cân tại \(B\), \(AB = a\) và \(SA = a\sqrt 3 \). Số đo theo đơn vị độ của góc nhị diện \(\left[ {A,\,BC,\,S} \right]\) là
\(60^\circ \).
\(135^\circ \).
\(90^\circ \).
\(45^\circ \).
Cho hình chóp tứ giác đều\(S.ABCD\) có \(O\) là tâm của đáy\(ABCD\). Gọi \(M\) là trung điểm của \(BC\) và \(K\) là hình chiếu vuông góc của \(O\) trên \(SM\). Khoảng cách từ \(O\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
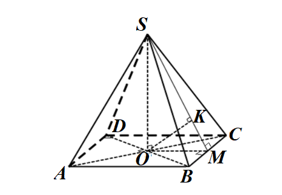
\(OK.\)
\(OB.\)
\(SO.\)
\(OM.\)
Cho hình lập phương \(ABCD.A'B'C'D'\). Mặt phẳng nào sau đây vuông góc với mặt phẳng \(\left( {ABCD} \right)\)?
\(\left( {A'B'C'D'} \right)\).
\(\left( {A'ADD'} \right)\).
\(\left( {C'BA'} \right)\).
\(\left( {ACD'} \right)\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(C\). Góc giữa đường thẳng \(SC\)và mặt phẳng \(\left( {ABC} \right)\)là
\(\widehat {SAC}\).
\(\widehat {SCB}\).
\(\widehat {SCA}\).
\(\widehat {SBA}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Gọi \(I\) là trung điểm của \(SC\) (tham khảo hình bên).
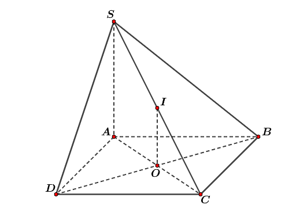
Khẳng định nào sau đây sai?
\(BD \bot \left( {SAC} \right).\)
\(IO \bot \left( {ABCD} \right).\)
\(AC \bot \left( {SBD} \right).\)
Hình chiếu vuông góc của điểm \[S\] lên \[\left( {ABCD} \right)\] là điểm \[A.\]
Cho hìnhchóp \(S.ABCD\) có đáy là hình chữ nhật, cạnh bên \(SA\) vuông góc với đáy (tham khảo hình bên)
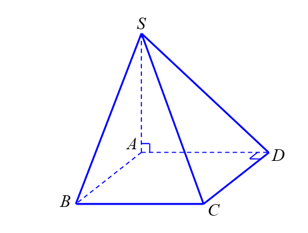
Khẳng định nào sau đây sai?
\(CD \bot SC.\)
\(CD \bot SA.\)
\[BC \bot AB.\]
\(SA \bot AB.\)
Cho hình lập phương \(ABCD.A'B'C'D'\)(tham khảo hình bên). Góc giữa hai đường thẳng \(BA'\) và \(CD\) bằng
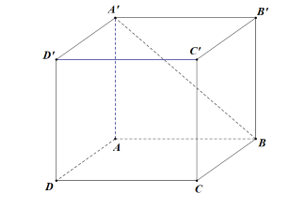
\(45^\circ \).
\(90^\circ \).
\(30^\circ \).
\(60^\circ \).
Cho khối chóp tứ giác đều \(S.ABCD\)có cạnh đáy bằng \(a\sqrt 3 \) và tam giác \(SBD\) đều.
Thể tích của khối chóp đã cho bằng
\[V = \frac{{{a^3}}}{2}\].
\[V = \frac{{3{a^3}\sqrt 2 }}{2}\].
\[V = \frac{{{a^3}\sqrt {18} }}{6}\].
\[V = \frac{{9{a^3}\sqrt 6 }}{2}\].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA \bot \left( {ABCD} \right)\). (Tham khảo hình vẽ )
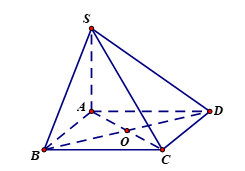
a) Đường thẳng \(CD\) và đường thẳng \(SA\) vuông góc với nhau.
b) Góc giữa đường thẳng \(BC\) và đường thẳng \(SD\) bằng góc giữa thẳng \(AD\) và đường thẳng \(SD\).
c) Đường thẳng \(BD\) vuông góc với mặt phẳng \(\left( {SAC} \right)\).
d) \(\widehat {SCA}\) là góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {SAD} \right)\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA = a\sqrt 2 \) và vuông góc với mặt đáy \(\left( {ABCD} \right)\).
a) Hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right)\) vuông góc với nhau.
b) Đường thẳng \(CD\)vuông góc với mặt phẳng \[\left( {SAD} \right)\].
c) Tam giác \(ABC\) là hình chiếu của tam giác \(SCB\) lên mặt phẳng \(\left( {ABCD} \right)\).
d) Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\).
Cho lăng trụ đứng \(ABC.A'B'C'\) có \[AC = a,\,\,BC = 2a,\,\,\widehat {ACB} = 120^\circ \] có thể tích \(V\). Gọi \(M\) là trung điểm của \(BB'\).
a) Số đo của góc nhị diện \(\left[ {A,CC',B} \right]\) bằng \(60^\circ \).
b) Biết khoảng cách giữa hai mặt đáy lăng trụ bằng \(2a\). Khi đó \(V = {a^3}\sqrt 3 \).
c) \({V_{M.ABC}} = \frac{1}{6}V\).
d) \(d\left( {C',\left( {ABB'A'} \right)} \right) = \frac{{a\sqrt {21} }}{7}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật tâm \(O\), đường thẳng \(SA\) vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\), \(SA = 2a\sqrt 3 \), \(AB = a\), \(AD = 2a\).
a)Đường thẳng \(BC\) vuông góc với mặt phẳng \(\left( {SAB} \right)\).
b)Mặt phẳng \(\left( {SAC} \right)\) vuông góc với mặt phẳng \(\left( {SBD} \right)\).
c)Số đo của góc nhị diện \(\left[ {A,DC,S} \right]\) bằng \(30^\circ \).
d)Gọi \(\alpha \) là góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {SAD} \right)\). Khi đó \(\cos \alpha = \frac{4}{{\sqrt {17} }}\).
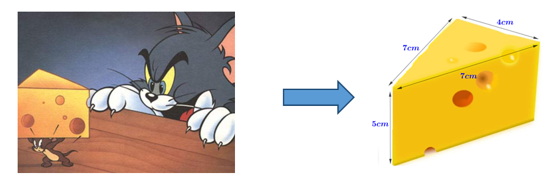
Cuộc tranh đuổi giữa chú chuột Jerry và mèo Tom để lấy miếng pho mát. Biết rằng miếng pho mát có dạng khối lăng trụ đứng chiều cao \(5\,{\rm{cm}}\) và độ dài các cạnh đáy lần lượt là \(7\,{\rm{cm}},7\,{\rm{cm,}}\)\(4\,{\rm{cm}}\). Tính thể tích của khối pho mát trên (kết quả làm tròn đến hàng phần mười của centimét khối).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), tam giác \(SAB\) là tam giác cân và nằm trong mặt phẳng vuông góc với đáy, gọi \(H\) là trung điểm cạnh \(AB\), khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SCD} \right)\) là \(a\sqrt 2 \), gọi \(\alpha \) là góc giữa đường thẳng \(SD\) và mặt phẳng đáy. Tính giá trị của biểu thức \[M = 25{\tan ^2}\alpha + 4{\cot ^2}\alpha \].
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng \(5\sqrt 2 \), tam giác \(SAD\) vuông cân tại \(S\) và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right)\). Tính khoảng cách giữa hai đường thẳng \(CD\) và \(SB\).
Cho khối chóp\(S.ABCD\) có đáy là hình vuông cạnh \(12\) và \(SA \bot \left( {ABCD} \right)\). Biết rằng khoảng cách giữa hai đường thẳng \(AB\) và \(SD\) bằng \(6\sqrt 2 \), tính thể tích khối chóp \(S.ABCD\).
Một đèn thả gỗ có dạng hình chóp cụt đều như hình bên. Đáy và mặt trên là các hình vuông tương ứng có cạnh bằng \(40{\rm{cm, 20cm}}\), cạnh bên của đèn dài \(10\sqrt 5 \,{\rm{cm}}\). Mặt bên và mặt trên của đèn tạo thành góc nhị diện có số đo bằng bao nhiêu độ?

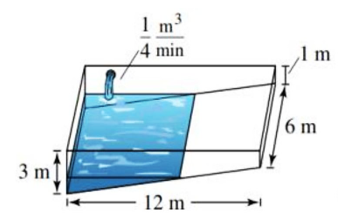
Một hồ bơi được chế tạo từ một khối hộp chữ nhật có chiều dài 12 mét, rộng 6 mét, sâu 1 mét ở đầu nông và sâu 3 mét ở đầu sâu (như hình vẽ). Nước được bơm vào hồ bơi với tốc độ 0,25 mét khối mỗi phút. Biết rằng trong bể có 1 mét nước ở đầu sâu. Để lượng nước đạt \(75{\rm{\% }}\) dung tích bể bơi thì cần bơm trong thời gian bao nhiêu phút?