Đề ôn luyện Toán Chương 2. Nguyên hàm và tích phân (đề số 2)
22 câu hỏi
Hàm số \(F\left( x \right) = {e^{{x^3}}}\) là nguyên hàm của hàm số nào trong các hàm số sau?
\(f\left( x \right) = 3{x^2} \cdot {e^{{x^3}}}\).
\(f\left( x \right) = {x^2} \cdot {e^{{x^3}}}\).
\(f\left( x \right) = {e^{3{x^2}}}\).
\(f\left( x \right) = \frac{{{e^{{x^3}}}}}{{3{x^2}}}\).
Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{{{x^2}}}{2} + 2x - 5\) là
\(\frac{{2{x^3}}}{3} + {x^2} - 5x + C\).
\(\frac{{{x^3}}}{3} + {x^2} - 5x + C\).
\[\frac{{{x^3}}}{6} + {x^2} - 5x + C\].
\[\frac{{{x^3}}}{6} + {x^2} - 5x\].
Họ tất cả các nguyên hàm của \[f\left( x \right) = {x^2} + \sin 2x\] là
\(2x + 2\cos 2x + C\).
\(2x - 2\cos 2x + C\).
\(\frac{{{x^3}}}{3} - \frac{1}{2}\cos 2x + C\).
\(\frac{{{x^3}}}{3} + \frac{1}{2}\cos 2x + C\).
Cho hàm số \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{\sqrt x }}\). Biết \(F\left( 1 \right) = 1\), tính \(F\left( 4 \right)\)ta được kết quả là
\(7\).
\(2\).
\(5\).
\(3\).
Tính tích phân \(\int\limits_0^1 {\left( {{2^x} \cdot {{\rm{3}}^x}} \right){\rm{d}}x} \) ta được kết quả là
\(\frac{5}{{\ln 6}}\).
\(\frac{6}{{\ln 6}}\).
\(\frac{7}{{\ln 6}}\).
\(\frac{8}{{\ln 18}}\).
Kết quả phép tính \(I = \int\limits_1^2 {\frac{{{x^2} + 2x + 3}}{x}{\rm{d}}x} \) bằng
\(I = 6 + 3\ln 2\).
\(I = \frac{5}{2} - 3\ln 2\).
\(I = \frac{3}{2} - 3\ln 2\).
\(I = \frac{7}{2} + 3\ln 2\).
Kết quả của tích phân \(\int\limits_0^{\frac{\pi }{2}} {\left( {2\sin x + 3\cos x} \right){\rm{d}}x} \) là
\( - 1\).
\(1\).
\(0\).
\(5\).
Biết \(\int\limits_1^3 {f\left( x \right){\rm{d}}x} = 5\) và \(\int\limits_1^3 {g\left( x \right){\rm{d}}x} = - 7\). Giá trị của \(\int\limits_1^3 {\left[ {3f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} \) bằng
\[ - 29\].
\[ - 31\].
\[1\].
\[29\].
Diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y = 3{x^2} + 1\), trục hoành và hai đường thẳng \(x = 0,x = 2\)bằng
\(8\).
\(12\).
\(10\).
\(9\).
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số\(f\left( x \right) = {2^x}\), \(g\left( x \right) = - x + 6\)và hai đường thẳng \(x = 0\), \(x = 2\) (xem hình bên) bằng
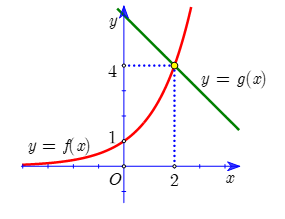
\[10 + \frac{3}{{\ln 2}}\].
\[10 - \frac{3}{{\ln 2}}\].
\[10 - \frac{4}{{\ln 2}}\].
\[10 + \frac{4}{{\ln 2}}\].
Khi cắt một vật thể bởi mặt phẳng vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\]\[\left( { - \sqrt 3 \le x \le \sqrt 3 } \right)\], mặt cắt là hình vuông có độ dài các cạnh là \[\sqrt {3 - {x^2}} \]. Thể tích của vật thể đã cho bằng
\(\sqrt 3 \).
\(4\sqrt 3 \).
\(4\pi \sqrt 3 \).
\(\pi \sqrt 3 \).
Cho hàm số\(y = \sqrt {{x^3} - 3} \) có đồ thị hàm số được biểu diễn trong hình bên. Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số trên và hai đường thẳng \(x = 2\) và \(x = 3\). Thể tích khối tròn xoay được tạo thành khi quay \(D\) quanh trục \(Ox\) bằng
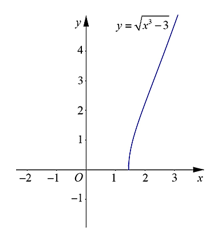
\(3,56\pi \).
\(\frac{{53}}{4}\pi \).
\(\frac{{53}}{4}\).
\(3,56\).
Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm \(t\) là \(h\left( t \right)\), trong đó \(t\) tính bằng phút, \(h\left( t \right)\) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số \(v\left( t \right) = - 0,12{t^2} + 1,2t\) với \(v\left( t \right)\) tính bằng mét/phút. Tại thời điểm xuất phát \(\left( {t = 0} \right)\) khinh khí cầu ở độ cao \(520\)m.
a)\(h\left( t \right) = - 0,04{t^3} + 0,6{t^2}\,\,\,\left( {0 \le t \le 29} \right)\).
b) Tại thời điểm \(t = 3\) phút, độ cao của khinh khí cầu là 524,32 m.
c) Độ cao tối đa của khinh khí cầu khi bay là 540 m.
d) Sau 15 phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
Để đảm bảo an toàn khi lưu thông trong thành phố thì các xe khi dừng lại phải cách nhau một khoảng tối thiểu là 1 m. Một xe máy di chuyển trên đường thì gặp đèn đỏ từ xa, người điều khiển xe máy đạp phanh và xe chuyển động chậm dần đều với vận tốc \(v\left( t \right) = 10 - 5t\,\,\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc đạp phanh.
a) Gia tốc tức thời của chuyển động này là \(5\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}\).
b) Thời gian kể từ lúc đạp phanh đến khi xe máy dừng hẳn là 2 giây.
c) Quãng đường xe máy đi được sau 0,5 giây kể từ lúc đạp phanh là 6 m.
d) Để giữ khoảng cách an toàn, người điều khiển xe máy phải bắt đầu đạp phanh khi cách xe đang dừng phía trước tối thiểu một khoảng 11 m (giả sử ngay lúc đạp phanh thì xe phía trước đang đứng yên).
Giả sử rằng khi tăng \(t\) năm tuổi, một máy công nghiệp \(A\) tạo ra doanh thu với tốc độ \(R'\left( t \right) = 650 - 3{t^2}\)(triệu đồng/năm), thời điểm \(t = 0\) tính từ lúc máy \(A\) bắt đầu hoạt động. Biết rằng chi phí biên cho vận hành và bảo trì là \(C'\left( t \right) = 48 + 12{t^2}\)(triệu đồng/năm), ở đây \(C\left( t \right)\) là chi phí vận hành và bảo trì của máy\(A\)khi nó được \(t\) năm tuổi.
a) Doanh thu sau 12 năm của máy\(A\)là \(\int\limits_0^{12} {\left( {650 - 3{t^2}} \right){\rm{dt}}} \) (triệu đồng).
b) Tổng chi phí vận hành và bảo trì của máy \(A\) trong 6 năm là 1152 (triệu đồng).
c) Tuổi thọ hữu ích của một máy là số năm T trước khi lợi nhuận (bằng doanh thu trừ chi phí) mà nó tạo ra bắt đầu giảm. Tuổi thọ hữu ích của máy \(A\) này là 8 năm.
d) Lợi nhuận do máy \(A\) tạo ra trong suốt thời gian tuổi thọ hữu ích của nó là 2532 triệu đồng.
Gọi H là hình phẳng giới hạn bởi các đồ thị hàm số \(y = \sqrt x ,y = 2{e^x}\) và hai đường thẳng \(x = 0,x = 4.\)
a) Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \sqrt x \), trục hoành và hai đường thẳng \(x = 0,x = 4\) là \(S = \pi \int\limits_0^4 {x\,{\rm{d}}x} \).
b) Gọi \[V\] là thể tích của khối tròn xoay giới hạn bởi đồ thị hàm số \(y = 2{e^x}\), trục hoành và hai đường thẳng\(x = 0,x = 4\) khi quay quanh trục \(Ox.\) Khi đó, \(V = 2\pi \left( {{e^8} - 1} \right)\).
c) Diện tích của hình H là \({S_H} = 2{e^4} - \frac{{16}}{3}\).
d) Thể tích khối tròn xoay giới hạn bởi hình H khi quay quanh trục Ox là \(2\pi \left( {{e^8} - 5} \right)\).
Một hồ bơi có dạng hình hộp chữ nhật có chiều cao \[3\,{\rm{m}}\] đang không chứa nước. Người ta cần thay nước mới cho hồ bơi nên dùng máy bơm để bơm nước vào hồ, giả sử \[h\left( t \right)\,\,({\rm{m)}}\] là chiều cao của mực nước đã được bơm vào tại thời điểm \[t\] giờ. Biết rằng tốc độ tăng chiều cao của mực nước tại giờ thứ \[t\] kể từ lúc bắt đầu bơm nước vào hồ là \[h'\left( t \right) = \frac{{\sqrt[3]{{t + 3}}}}{5}\]. Hỏi sau bao nhiêu giờ kể từ lúc bắt đầu bơm thì hồ đạt được độ sâu \[2,1\,{\rm{m}}\](kết quả làm tròn đến hàng đơn vị).
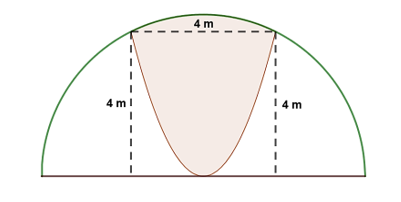
Khuôn viên nhà bạn Thùy Dương có dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn và cách nhau một khoảng bằng 4 m. Phần còn lại của khuôn viên dành để trồng cỏ nhung Nhật. Biết các kích thước cho như hình vẽ, chi phí trồng hoa và cỏ nhung Nhật tương ứng là 250 000 đồng/m2 và 150 000 đồng/m2. Hỏi chi phí để trồng hoa và trồng cỏ nhung Nhật trong khuôn viên đó hết bao nhiêu triệu đồng (làm tròn kết quả đến hàng phần chục)?
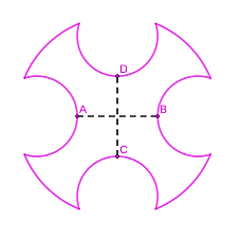
Trong cơ khí chế tạo, một chi tiết máy hình đĩa tròn có dạng như hình vẽ, nhận \[AB\] và \[CD\] làm các trục đối xứng. Người ta cần phủ sơn cả hai mặt của chi tiết. Biết rằng đường tròn lớn có bán kính \[5\,{\rm{dm}}\], các đường tròn nhỏ đều có bán kính bằng \[2\,{\rm{dm}}\], \[AB = CD = 4\,{\rm{dm}}\]và chi phí sơn là 82 000 đồng/\[{{\rm{m}}^{\rm{2}}}\]. Chi phí để sơn hoàn thiện chi tiết máy bằng bao nhiêu nghìn đồng (kết quả làm tròn đến hàng đơn vị)?
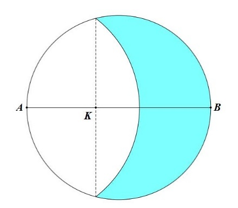
Một khối tròn xoay được tạo thành khi quay hình phẳng \(\left( H \right)\) (phần tô đậm trong hình vẽ) quanh trục \(AB\).
Miền \(\left( H \right)\) được giới hạn bởi đường tròn đường kính \(AB\) và cung tròn tâm \(A\). Biết \(AB = 8{\rm{ cm}}\) và điểm \(K\) trong hình vẽ thỏa mãn \(AK = 3{\rm{ cm}}\). Thể tích của khối tròn xoay đó bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng đơn vị)?
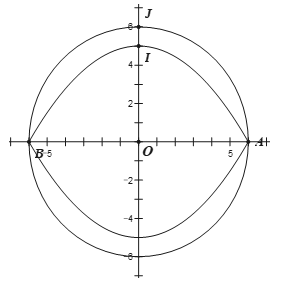
Khu vực trung tâm một quảng trường (xem hình vẽ bên) có dạng hình tròn đường kính \(AB\) bằng \(12\,{\rm{m}}\). Người ta trang trí khu vực này bằng hai đường parabol đối xứng nhau qua \(AB\), nằm trong hình tròn, đi qua các điểm \(A,\,B\) và có đình cách mép hình tròn \(1\,{\rm{m}}\). Phần giới hạn bởi hai parabol được trồng hoa với chi phí \(300\) nghìn đồng mỗi mét vuông, phần còn lại được lát gạch gốm sứ với chi phí \(900\) nghìn đồng mỗi mét vuông. Tổng chi phí để hoàn thành khu vực này là bao nhiêu triệu đồng? (kết quả làm tròn đến hàng đơn vị).
Một nhà kho có dạng khối hộp chữ nhật cùng phần mái phía trên được thiết kế dạng vòm cong. Chiều dài của nhà kho là 40 m, chiều rộng 10 m, chiều cao 5 m; đường cắt của mái vòm khi cắt bởi mặt phẳng vuông góc với chiều dài của kho là một cung tròn, điểm cao nhất của mái vòm có chiều cao là 6 m (hình vẽ minh họa).
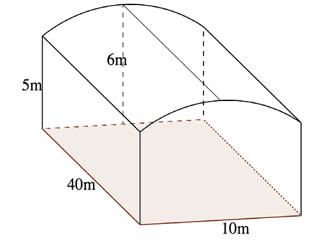
Để tính toán công suất cho hệ thống làm lạnh nhà kho, người ta cần ước lượng thể tích phần không gian bên trong nhà kho. Hãy cho biết thể tích không gian bên trong nhà kho là bao nhiêu mét khối (kết quả làm tròn đến hàng đơn vị)?

