Đề ôn luyện Toán Chương 2. Nguyên hàm và tích phân (đề số 1)
22 câu hỏi
Nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = 2\sin x - \cos x\) thỏa mãn \(F\left( {\frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{2}\) là
\(F\left( x \right) = 2\cos x - \sin x - 1\).
\(F\left( x \right) = 2\cos x + \sin x - 1 - \sqrt 3 \).
\(F\left( x \right) = - 2\cos x - \sin x + 1\)
\(F\left( x \right) = - 2\cos x - \sin x - 1\).
Họ các nguyên hàm của hàm số \(f\left( x \right) = {{\rm{e}}^{3x}} + 1\) là
\[3{{\rm{e}}^{3x}} + C\].
\[\frac{1}{3}{{\rm{e}}^{3x}} + C\].
\[3{{\rm{e}}^{3x}} + x + C\].
\[\frac{1}{3}{{\rm{e}}^{3x}} + x + C\].
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) = {x^2} - 2x - 3\) và \(f\left( 0 \right) = 1\). Khi đó \(f\left( x \right)\) bằng
\[\frac{{{x^3}}}{3} - {x^2} - 3x + 2\].
\[\frac{{{x^3}}}{3} - {x^2} - 3x + 3\]
\[\frac{{{x^3}}}{3} - {x^2} - 3x + 1\].
\[\frac{{{x^3}}}{3} - {x^2} - 3x\].
Nguyên hàm của hàm số \(f\left( x \right) = {2^x} + x\) là
\({2^x} + \frac{{{x^2}}}{2} + C\).
\({2^x} + {x^2} + C\).
\(\frac{{{2^x}}}{{\ln 2}} + {x^2} + C\).
\(\frac{{{2^x}}}{{\ln 2}} + \frac{{{x^2}}}{2} + C\).
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;\,10} \right]\) và \(\int\limits_0^{10} {f\left( x \right){\rm{d}}x = 7} \) và \(\int\limits_2^6 {f\left( x \right){\rm{d}}x = 3} \). Tính \(P = \int\limits_0^2 {f\left( x \right){\rm{d}}x + \int\limits_6^{10} {f\left( x \right){\rm{d}}x} } \).
\(P = 7\).
\(P = - 4\).
\(P = 4\).
\(P = 10\).
Tính \(\int\limits_1^3 {\frac{{2{x^2} + 1}}{x}{\rm{d}}x} \) được kết quả là
\(8 - \ln 3\).
\(8 + 2\ln 3\).
\(8 + \ln 3\).
\(7 + \ln 3\).
Tính \(\int\limits_0^{\frac{\pi }{6}} {{\rm{cos}}\,x\,{\rm{d}}x} \) được kết quả là
\( - 1\).
\( - \frac{1}{2}\).
\(\frac{1}{2}\).
\(1\).
Kết quả phép tính \(\int\limits_1^2 {{3^x}{\rm{d}}x} \)bằng
\(\frac{2}{{\ln 3}}\).
\(6\).
\(\frac{{ - 6}}{{\ln 3}}\).
\(\frac{6}{{\ln 3}}\).
Biết rằng \(\int\limits_1^3 {f\left( t \right){\rm{d}}t} = 4\). Tính \(\int\limits_1^3 {2f\left( x \right){\rm{d}}x} \) ta được kết quả là
\(2\).
\(6\).
\(4\).
\(8\).
Diện tích của hình phẳng giới hạn bởi các đường \(y = \cos x,\;y = x + 1,\;x = \frac{\pi }{2},\;x = \pi \) (tham khảo hình bên) bằng
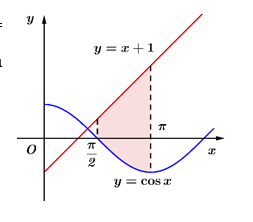
\(\frac{{3{\pi ^2} - 4\pi + 8}}{8}\).
\[\frac{{3{\pi ^2} + 4\pi + 8}}{2}\] .
\(\frac{{3{\pi ^2} + 4\pi + 8}}{6}\).
\(\frac{{3{\pi ^2} + 4\pi + 8}}{8}\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {e^x},\] trục hoành và hai đường thẳng \[x = 0\] và \[x = 3\] bằng
\({e^3}.\)
\({e^3} - 1.\)
\({e^2} - 1.\)
\(e\left( {{e^2} - 1} \right).\)
Cho hình phẳng \(\left( S \right)\) giới hạn bởi đồ thị hàm số \(y = \sqrt {2 - {x^3}} \), trục hoành và hai đường thẳng \(x = - 1\) và \(x = 1\). Thể tích của khối tròn xoay khi quay \(\left( S \right)\) quanh \(Ox\)là
\(\frac{{58}}{7}\pi \).
\(4\pi \).
\(\frac{{20}}{7}\pi \).
\(\frac{{27}}{6}\pi \).
Trong dây chuyền sản xuất sữa chua hiện đại của một nhà máy thực phẩm, từng giọt sữa chua âm thầm chuyển mình dưới tác động của hàng triệu vi khuẩn Lactic, những “nghệ nhân tí hon” kiến tạo vị chua thanh đặc trưng. Mật độ vi khuẩn (số triệu tế bào trên mỗi ml sữa chua) tại thời điểm \(t\) (giờ) được kí hiệu là \(N\left( t \right)\). Ban đầu (\(t = 0\) giờ), mật độ vi khuẩn đo được là \(N\left( 0 \right) = 10\) triệu tế bào/ml. Do sự thay đổi về nguồn dinh dưỡng (đường lactose giảm) và độ pH (axit lactic tăng) nên tốc độ thay đổi mật độ vi khuẩn \(N'\left( t \right)\) (đơn vị: triệu tế bào/ ml mỗi giờ) được mô hình hóa bởi công thức \(N'\left( t \right) = 18t - 3{t^2}\) (triệu tế bào/ml mỗi giờ) với \(t\) là thời gian tính bằng giờ \(\left( {0 \le t \le 7} \right)\).
a)\(N'\left( 1 \right) = 15\) triệu tế bào/ml giờ.
b)
c) So với lúc ban đầu (\(t = 0\)), mật độ vi khuẩn đã tăng thêm 108 triệu tế bào/ml khi đến thời điểm \(t = 6\) giờ.
d) Tại thời điểm \(t = 7\) giờ, mật độ vi khuẩn trong 1 ml sữa chua là 108 triệu tế bào/ml.
Một ô tô đang di chuyển với vận tốc \(21\,\,{\rm{m/s}}\), khi còn cách trạm thu phí một đoạn thì người lái xe bắt đầu đạp phanh lần một, xe chuyển động thẳng chậm dần đều với vận tốc biến thiên theo thời gian được xác định bởi quy luật \({v_1}\left( t \right) = - 6t + 21\,\,\left( {{\rm{m/s}}} \right)\), trong đó thời gian \(t\) tính bằng giây, đến đúng trạm thu phí thì xe dừng hẳn. Sau khi trả phí, xe ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \({v_2}\left( t \right) = 5t\,\,\left( {{\rm{m/s}}} \right)\), đi được \(4\)giây, ô tô gặp chướng ngại vật nên phải phanh gấp lần hai.
a) Thời gian từ lúc ô tô phanh lần một cho đến khi dừng hẳn ở trạm thu phí là \(3\)giây.
b) Quãng đường ô tô đi được từ lúc đạp phanh đến khi dừng ở trạm thu phí là \(36,75\,\,{\rm{m}}\).
c) Vận tốc của ô tô tại thời điểm người tài xế phanh gấp lần hai là \(20\,{\rm{m/s}}\).
d) Tổng quãng đường ô tô chuyển động từ lúc phanh lần một đến lúc phanh lần hai là \(76,75\,{\rm{m}}{\rm{.}}\)
Cho đồ thị hàm số \(y = {x^3} - 2{x^2} - 3x + 4\,\left( C \right)\)và đường thẳng \(d:y = 2x - 2\).
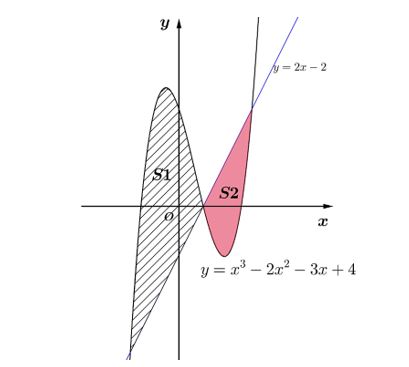
a) Đường thẳng \(d\) cắt đồ thị \(\left( C \right)\) tại ba điểm \(A\left( { - 2; - 6} \right),\,B\left( {1;0} \right),\,C\left( {3;4} \right)\).
b) Diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right)\), trục hoành, đường thẳng \(x = - 1,\,x = 2\)bằng \(\frac{{21}}{4}\).
c) Biết đường thẳng \(d\) cắt đồ thị \(\left( C \right)\) thành hai miền \({S_1}\) và \({S_2}\). Tỉ số \(\frac{{{S_1}}}{{{S_2}}} = \frac{{63}}{{16}}\).
d) Diện tích hình phẳng giới hạn bởi đồ thị \(\left( C \right)\) và đường thẳng \(d\) bằng \(\frac{{253}}{{12}}\).
Một chất điểm chuyển động trên đường thẳng với vận tốc \[v\left( t \right),{\rm{ }}0 \le t \le 5\] (\[t\]có đơn vị là giây và \[v\left( t \right)\] có đơn vị mét/giây). Hàm số \[v\left( t \right)\] có đồ thị gồm hai đoạn thẳng \[OB,BC\] và đường cong \[CD\] là một phần parabol \[v\left( t \right) = a{t^2} + bt + c,{\rm{ }}\left( {a,b,c \in \mathbb{R}} \right)\] có đỉnh \[C\] (như hình vẽ).
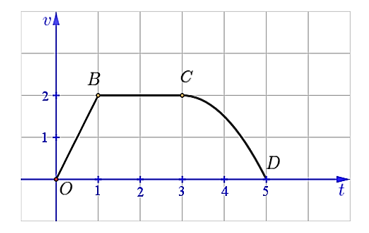
a) Trong một giây đầu tiên, vận tốc của chất điểm là \[v\left( t \right) = 2t,{\rm{ }}0 \le t \le 1\].
b) Quãng đường chất điểm đi được trong hai giây đầu tiên là \[2{\rm{ m}}\].
c) Giá trị của \[b\] và\[c\] lần lượt là \[b = 3,c = - \frac{5}{2}\].
d) Quãng đường chất điểm đi được trong khoảng thời gian \[5\] giây là \[7,7{\rm{ m}}\] (kết quả được làm tròn đến hàng phần mười).
Một chất điểm chuyển động trên đường thẳng nằm ngang với gia tốc phụ thuộc thời gian \(t\)(s) là \(a\left( t \right) = 2t - 7\)(m/s2). Biết vận tốc đầu bằng 10 (m/s), hỏi sau bao lâu thì chất điểm đạt vận tốc 18 (m/s)?
Một bác thợ xây bơm nước vào bể chứa nước. Gọi \[h\left( t \right)\] là thể tích nước bơm được sau \[t\] phút. Biết \[h'\left( t \right) = 3a{t^2} + bt\] và ban đầu bể không có nước. Sau \(5\) phút thì thể tích nước trong bể là \[150\,\,{\rm{d}}{{\rm{m}}^{\rm{3}}}\], sau \(10\) phút thì thể tích nước trong bể là \[1100\,\,{\rm{d}}{{\rm{m}}^{\rm{3}}}\]. Thể tích của nước trong bể sau khi bơm được \(20\) phút là bao nhiêu decimét khối?
Một dụng cụ đựng nước có dạng như hình bên. Nếu cắt dụng cụ bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng \(x\)(cm) \((0 \le x \le 5)\) thì được thiết diện là hình chữ nhật có chiều dài là \(2x\) (cm) và chiều rộng là \(\sqrt {x + 3} \)(cm). Dung tích của dụng cụ trên là bao nhiêu centimét khối (kết quả làm tròn đến chữ số thập phân hàng phần chục)?
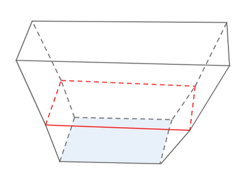
Một biển quảng cáo có dạng hình vuông \[ABCD\] cạnh bằng \[4{\rm{ m}}\] và \(I\) là trung điểm của đoạn thẳng \(CD\). Trên tấm biển đó có đường parabol đỉnh \(I\) đi qua \(A,B\) và cắt đường chéo \(BD\) tại \(M\) (\(M\) khác \(B\), tham khảo hình vẽ).
Người ta cần sơn tấm biển quảng cáo, biết rằng chi phí sơn phần hình gạch sọc (có diện tích \({S_1}\)) là \[200\,000\] đồng/m², chi phí sơn phần tô đậm (có diện tích \({S_2}\)) là \[180\,000\] đồng/m² và phần còn lại là \[150\,000\] đồng/m². Số tiền cần chi trả để sơn tấm biển quảng cáo là bao nhiêu nghìn đồng?
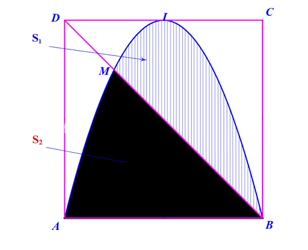
Một kiến trúc sư chịu trách nhiệm thiết kế một tòa nhà cao 30 mét. Mặt cắt ngang tại mọi độ cao, vuông góc với trục thẳng đứng, luôn là một hình vuông (xem hình vẽ).
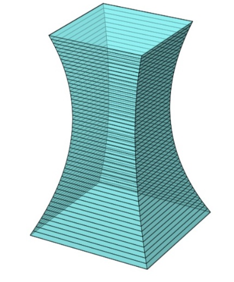
Mặt đáy tòa nhà là hình vuông có cạnh \({L_0} = 26\;{\rm{m,}}\) mặt đỉnh là hình vuông có cạnh \({L_{30}} = 20\;{\rm{m}}{\rm{.}}\)Mặt cắt ngang tại vị trí hẹp nhất của tòa nhà là hình vuông có cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\) Mặt cắt của tòa nhà theo mặt phẳng đứng chứa đường chéo đáy có dạng là hình phẳng giới hạn bởi hai đường cong parabol đối xứng nhau qua trục thẳng đứng đi qua tâm đáy của tòa nhà. Tính thể tích của tòa nhà đó (làm tròn đến hàng đơn vị, đơn vị tính: mét khối).
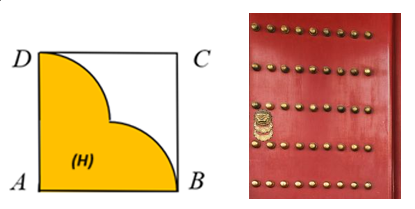
Trên cánh cửa được trang trí các núm có dạng một khối tròn xoay được đúc bằng chất liệu đồng, khuôn đúc của nó được tạo thành khi quay miền \(\left( H \right)\) (phần được tô màu trong hình vẽ) quanh trục \(AB\). Miền \(\left( H \right)\) được giới hạn bởi các cạnh \(AB\), \(AD\) của hình vuông \(ABCD\) và các cung phần tư của các đường tròn bán kính bằng \(1\) cm với tâm lần lượt là trung điểm của các cạnh \(AD\), \(AB\). Biết công thức tính khối lượng của một vật là \(P = V \cdot D\), trong đó \(P\) là khối lượng của vật (đơn vị gam), \(V\) là thể tích của vật (đơn vị \({\rm{c}}{{\rm{m}}^{\rm{3}}}\)) và \(D\) là khối lượng riêng của vật (đơn vị \({\rm{gam/c}}{{\rm{m}}^{\rm{3}}}\)), khối lượng riêng của đồng là \(D = 8,96\,{\rm{gam/c}}{{\rm{m}}^{\rm{3}}}\).Giá đồng trên thị trường là 200 000 đồng/kg. Giá tiền vật liệu để đúc một núm đồng trên là bao nhiêu nghìn đồng (kết quả làm tròn đến hàng đơn vị)?