Đề ôn luyện Toán Chương 1. Ứng dụng đạo hàm để khảo sát hàm số (đề số 2)
22 câu hỏi
Cho đồ thị hàm số \(y\, = \,f\left( x \right)\)như hình vẽ.
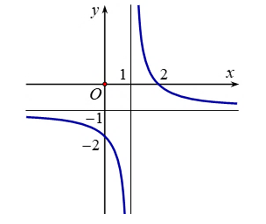
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ sau.
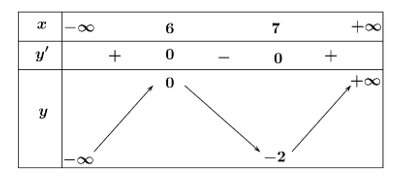
Tìm điểm cực đại của hàm số \(y = f\left( x \right)\).
\(x = 7\).
\(x = - 2\).
\(x = 0\).
\(x = 6\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\)như hình vẽ.
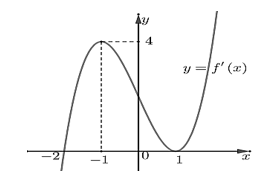
Khẳng định nào sau đây sai?
Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng \(\left( { - 2;\,1} \right)\).
Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng \(\left( { - 1;\,1} \right)\).
Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng \(\left( { - \infty ;\,\, - 2} \right)\).
Hàm số \[y = - {x^3} + 3{x^2}\] đồng biến trên khoảng nào dưới đây?
\[\left( {0;4} \right)\].
\[\left( { - \infty ;0} \right)\].
\[\left( {2; + \infty } \right)\].
\[\left( {0;2} \right)\].
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ { - 2\,;\,2} \right]\) và có đồ thị là đường cong trong hình vẽ sau.
![Cho hàm số y = f(x) xác định và liên tục trên đoạn [ -2; 2] và có đồ thị là đường cong trong hình vẽ sau (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/blobid0-1762223692.png)
Điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) là
\[x = 1\].
\[x = - 2\].
\[M\left( {1\,;\, - 2} \right)\].
\[M\left( { - 2\,;\, - 4} \right)\].
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) có đồ thị như hình vẽ.
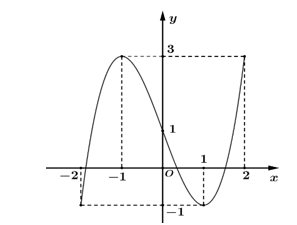
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 2;2} \right]\) là
\(1\).
\( - 1\).
\( - 2\).
\(3\).
Đồ thị hàm số \[y = \frac{{1 + 2x}}{{x - 1}}\]có đường tiệm cận ngang là
\(x = 1\).
\(y = 1\).
\(x = 2\).
\(y = 2\).
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x + 1}}\) là
\(y = x - 3\).
\(y = x + 1.\)
\(y = - 3x + 1.\)
\(x = - 3y + 1.\)
Đường cong ở hình sau là đồ thị của hàm số nào?
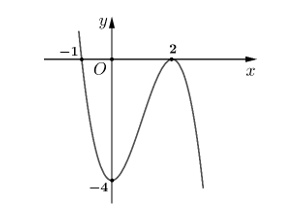
\[y = - {x^3} + 3{x^2} - 4.\]
\[y = {x^3} - 4.\]
\[y = {x^2} - 4.\]
\[y = - {x^2} - 4.\]
Cho hàm số \[y = f\left( x \right)\] có bảng xét dấu đạo hàm như sau:
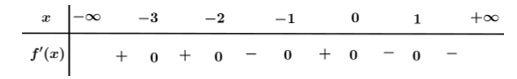
Giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên đoạn \[\left( { - 1; + \infty } \right)\] bằng
\[f\left( 1 \right)\].
\[f\left( { - 2} \right)\].
\[f\left( { - 1} \right)\].
\[f\left( 0 \right)\].
Cho hàm số \[y = \frac{{ax + b}}{{cx - 1}}\]có đồ thị như hình vẽ bên dưới.
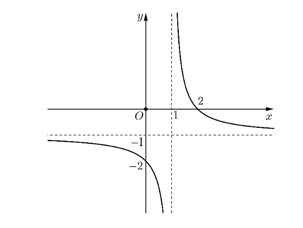
Giá trị của tổng \[S = a + b + c\]bằng:
\[S = 0\].
\[S = - 2\].
\[S = 2\].
\[S = 4\].
Cho hàm số \[y = \frac{{a{x^2} + bx + 1}}{{cx + 2}}\] có đồ thị như hình vẽ bên dưới.
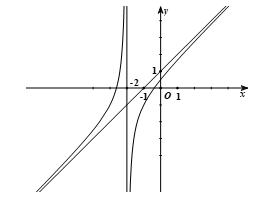
Tính giá trị biểu thức: \(T = 2a + 3b - c\).
9.
10.
8.
11.
Cho hàm số \(f\left( x \right) = \frac{1}{2}{x^2} + x - 6{\rm{ln}}\left( {x + 2} \right)\).
a) Đạo hàm của hàm số là \(f'\left( x \right) = x + 1 - \frac{6}{{x + 2}}\).
b) Trên đoạn \(\left[ { - 1;2} \right]\), phương trình \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
c) \(f\left( { - 1} \right) = - \frac{1}{2}\) và \(f\left( 2 \right) = 4 - 12{\rm{ln}}2\).
d) Giá trị nhỏ nhất của \(f\left( x \right)\) trên đoạn \(\left[ { - 1;2} \right]\) lớn hơn –5.
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm \[t\] (giây) là \[y = {t^3} - 12t + 3,\,\,t \ge 0\].
a) Hàm gia tốc của vật là \[a = y'\].
b) Hàm vận tốc của vật là \[v\left( t \right) = 3{t^2} - 12\].
c) Tại thời điểm \[t = 1\] thì hạt đang chuyển động lên trên.
d) Trong khoảng thời gian \[0 \le t \le 3\] thì quãng đường mà hạt đi là \[23\]m.
Nhà máy\(A\) chuyên sản xuất một loại sản phẩm cho nhà máy \(B\). Hai nhà máy thỏa thuận rằng, hằng tháng \(A\) cung cấp cho \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(x\) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm được biểu diễn bởi công thức: \(P\left( x \right) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để \(A\) sản xuất \(x\) tấn sản phẩm trong một tháng là \(C\left( x \right) = 100 + 30x\) triệu đồng (gồm \(100\)triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm).
a) Chi phí để \(A\) sản xuất \(10\) tấn sản phẩm trong một tháng là \(400\)triệu đồng.
b) Số tiền \(A\) thu được khi bán \(10\) tấn sản phẩm cho \(B\) là \(600\)triệu đồng.
c) Lợi nhuận mà \(A\) thu được khi bán \(x\) tấn sản phẩm \(\left( {0 \le x \le 100} \right)\) cho \(B\) được biểu diễn bởi công thức \(H\left( x \right) = - 0,001{x^3} + 15x - 100\)(triệu đồng).
d) Bên \(A\) bán cho \(B\) khoảng \(70,7\) tấn sản phẩmmỗi tháng thì thu được lợi nhuận lớn nhất.
Đường dây điện \[110\,{\rm{KV}}\] kéo từ trạm phát (điểm \[A\]) qua điểm G trong đất liền (với AB là bờ) ra Côn Đảo (điểm\[C\]). Biết \[BC = 60\,{\rm{km}}\], \[AB = 100\,{\rm{km}}\], \[\widehat {ABC} = 90^\circ \], như hình vẽ. Mỗi kilomet dây điện dưới nước chi phí là \[5000\,{\rm{USD}}\], chi phí cho mỗi kilomet dây điện trên bờ là \[3000\,\,{\rm{USD}}\]. Đặt \[x = AG\].
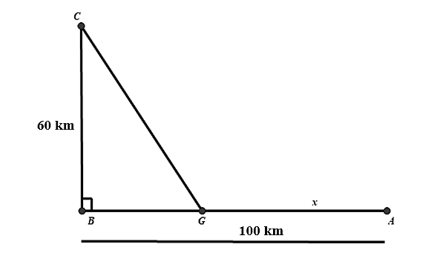
a) Khi \[x = 20\,{\rm{km}}\] thì đường dây điện nối từ \[C\] về \[G\] dài \[100\,{\rm{km}}\].
b) Khi \[x = 20\,{\rm{km}}\] thì tổng chi phí mắc điện là \[560000\,{\rm{USD}}\].
c) Tổng chi phí mắc điện nhỏ nhất khi \[x = 50\,{\rm{km}}\].
d) Tổng chi phí mắc điện nhỏ nhất là \[540000\,{\rm{USD}}\].
Gọi \(m,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{1}{2}x - \sqrt {x + 1} \) trên đoạn \(\left[ {0;3} \right]\). Tổng \(S = 2M - m\) bằng bao nhiêu?
Cho hàm số \(y = f\left( x \right)\) có đồ thị của \(f'\left( x \right)\) như hình vẽ bên dưới. Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
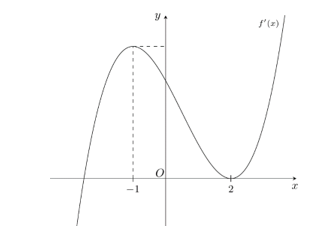
Cho đồ thị hàm số \(f\left( x \right) = \frac{{5{x^2} - 6x + 9}}{{x - 1}}\) có tâm đối xứng là \(I\left( {a\,;\,b} \right)\). Giá trị của biểu thức \(C = a + 3b\) là bao nhiêu?
Một cốc chứa \[25\]ml dung dịch NaOH với nồng độ \[100\] mg/ml. Một bình chứa dung dịch NaOH khác với nồng độ \[9\]mg/ml được trộn vào cốc. Gọi \[C\left( x \right)\] là nồng độ của NaOH sau khi trộn \[x\](ml) từ bình chứa, ta thấy nồng độ của NaOH trong cốc sẽ luôn giảm theo \[x\] nhưng luôn lớn hơn một số \[a\]. Tính \[a\].
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(G\left( x \right) = 0,035{x^2}\left( {15 - x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân (\(x\) được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
Từ một miếng tôn dạng nửa hình tròn có bán kính \[R = 4\]dm, người ta muốn cắt ra một hình chữ nhật. Hỏi diện tích lớn nhất của hình chữ nhật có thể cắt được là bao nhiêu decimet vuông?