Đề ôn luyện Toán Chương 1. Ứng dụng đạo hàm để khảo sát hàm số (đề số 1)
22 câu hỏi
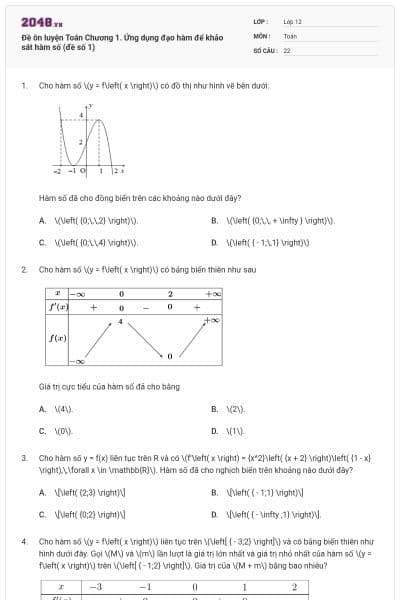
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới:
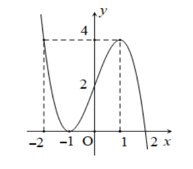
Hàm số đã cho đồng biến trên các khoảng nào dưới đây?
\(\left( {0;\,\,2} \right)\).
\(\left( {0;\,\, + \infty } \right)\).
\(\left( {0;\,\,4} \right)\).
\(\left( { - 1;\,1} \right)\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
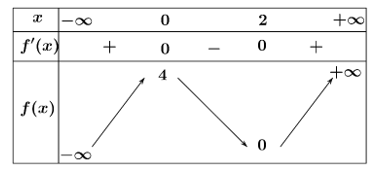
Giá trị cực tiểu của hàm số đã cho bằng
\(4\).
\(2\).
\(0\).
\(1\).
Cho hàm số y = f(x) liên tục trên R và có \(f'\left( x \right) = {x^2}\left( {x + 2} \right)\left( {1 - x} \right),\,\forall x \in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\[\left( {2;3} \right)\]
\[\left( { - 1;1} \right)\]
\[\left( {0;2} \right)\]
\[\left( { - \infty ;1} \right)\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;2} \right]\) và có bảng biến thiên như hình dưới đây. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left[ { - 1;2} \right]\). Giá trị của \(M + m\) bằng bao nhiêu?
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;2} \right]\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/screenshot-2025-11-04-082626-1762219471.png)
\(3\)
\(2\)
\(1\)
\(4\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{ - 2x + 3}}{{5x + 1}}\) là đường thẳng có phương trình
\(y = - \frac{1}{5}\)
\(x = - \frac{1}{5}\)
\(y = - \frac{2}{5}\)
\(x = - \frac{2}{5}\).
Giá trị lớn nhất của hàm số \[y = {x^3} - 3{x^2} + 3\] trên \[\left[ {0;3} \right]\] là
\[ - 2\].
\[2\].
\[3\].
\[ - 1\].
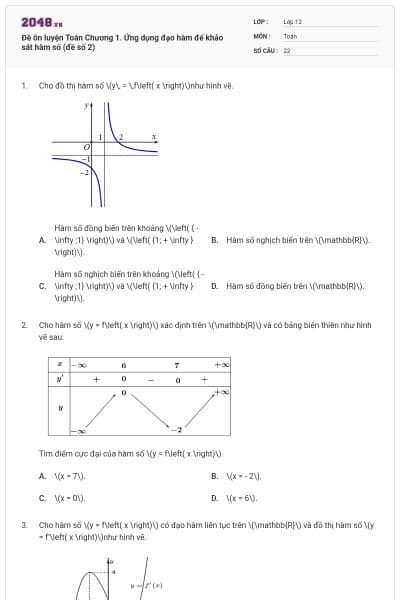
Hình bên là đồ thị của hàm số nào?
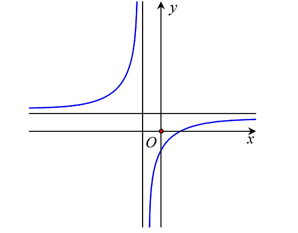
\(y = {x^3} - 3{x^2} + 1\).
\(y = \frac{{x - 1}}{{x + 1}}\)
\(y = \frac{{x + 2}}{{x + 1}}\)
\(y = - {x^4} + 2{x^2} + 1\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 2}}{{x + 2}}\) là
\(y = - 2\)
\(y = 1\).
\(y = 1\).
\(y = x\).
Điểm cực đại của đồ thị hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) là:
\(x = - 2\).
\(x = 0\).
\(\left( { - 2\,;\, - 2} \right)\).
\(\left( {0\,;\, - 2} \right)\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị trên đoạn \(\left[ { - 1;5} \right]\) như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\)bằng ![Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/blobid1-1762220427.png)
\( - 1\).
\(4\).
\(1\).
\(2\).
Cho hàm số \[y = f\left( x \right)\]có bảng biến thiên như sau:
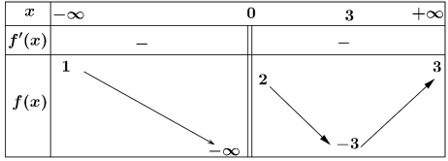
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
2.
3.
4.
1.
Cho hàm số \(f\left( x \right) = \frac{{ax - 6}}{{bx - c}}\)\(\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
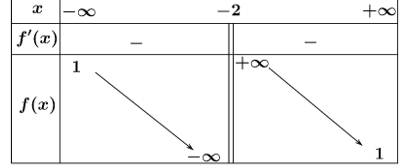
Trong các số \(a,b,c\) có bao nhiêu số âm?
\[3\].
\[1\].
\[2\].
\[0\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây.
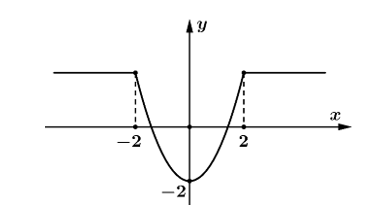
a) Hàm số \(f\left( x \right)\) không có đạo hàm tại \(x = - 2\) và \(x = 2\).
b) Hàm số \(f\left( x \right)\) có ba điểm cực trị.
c) Giá trị nhỏ nhất của hàm số \(f\left( x \right)\) bằng đạt được tại x= 0 .
d) Hàm số f(x) không có giá trị lớn nhất.
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 4x - 1}}{{x - 1}}\) có đồ thị là \(\left( C \right)\).
a)Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {3; + \infty } \right)\).
b) Đồ thị hàm số \(f\left( x \right)\) đạt cực đại tại điểm có toạ độ \(\left( { - 1\,;\,2} \right)\).
c) Đường thẳng \(x = 1\) là đường tiệm cận đứng của đồ thị hàm số \(f\left( x \right)\).
d) Phương trình đường tiệm cận xiên của đồ thị hàm số \(f\left( x \right)\) là \(y = 2x + 5\).
Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng \(480\) nghìn đồng trên \(1\) giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi \(v = 10\) (km/giờ) thì phần thứ hai bằng \(30\) nghìn đồng/giờ.
a) Khi vận tốc \(v = 10\)(km/giờ) thì chi phí nguyên liệu cho phần thứ nhất trên \(1\)km đường sông là 48000 đồng.
b) Hàm số xác định tổng chi phí nguyên liệu trên \(1\)km đường sông với vận tốc \(x\)(km/h) là\(f\left( x \right) = \frac{{480}}{x} + 0,03{x^3}\) (nghìn đồng).
c) Khi vận tốc \(v = 30\)(km/giờ) thì tổng chi phí nguyên liệu trên \(1\)km đường sông là 43000 đồng.
d)Vận tốc của tàu để tổng chi phí nguyên liệu trên \(1\)km đường sông nhỏ nhất là \(v = 20\)(km/giờ).
Người ta bơm xăng vào bình xăng của một xe ô tô. Biết rằng thể tích \[V\] (tính theo lít) của lượng xăng trong bình xăng được tính theo thời gian bơm xăng \(t\) (phút) được cho bởi công thức:
\(V\left( t \right) = 300\left( {{t^2} - {t^3}} \right) + 4,5\) với \(0 \le t \le 0,5\).
Gọi \(V'\left( t \right)\) là tốc độ tăng thể tích tại thời điểm \(t\) với \(0 \le t \le 0,5\). Biết 1 lít xăng có giá là 21 000 đồng.
a) Phương trình \(V'\left( t \right) = 0\) có hai nghiệm phân biệt trên đoạn \(\left[ {0\,;\,\frac{1}{2}} \right]\).
b) Lượng xăng ban đầu trong bình ban đầu là \(1,5\) lít.
c) Khi xăng chảy vào bình xăng thì tốc độ tăng thể tích là lớn nhất vào thời điểm ở giây thứ 21.
d) Sau khi bơm 30 giây thì bình xăng đầy. Số tiền người mua phải trả là 787 500 đồng.
Gọi \[m,n\] lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số \[y = \frac{{{x^2} + x + 4}}{{x + 1}}\]. Tính giá trị biểu thức \[P = {m^3} + {n^3}\].
Cho đồ thị hàm số \(y = f\left( x \right) = 4x - 3 + \frac{1}{{x - 2}}\) có tâm đối xứng \(I\left( {a;b} \right)\). Giá trị của biểu thức \(a - 3b\) là bao nhiêu?
Nếu trong một ngày, một xưởng sản xuất được \(x\) chiếc vợt cầu lông thì chi phí trung bình (tính bằng nghìn đồng) cho một chiếc vợt cầu lông được cho bởi công thức \(C\left( x \right) = \frac{{5x + 1}}{x}\). Xét trong một khoảng thời gian dài, xưởng sản xuất đã sản xuất được “rất nhiều” chiếc vợt cầu lông. Vậy cho đến nay, chi phí sản xuất mỗi chiếc vợt cầu lông là bao nhiêu nghìn đồng?
Một hãng điện thoại đưa ra quy luật bán buôn cho từng đại lí, đó là đại lí càng nhập nhiều chiếc điện thoại của hãng thì giá bán buôn một chiếc điện thoại càng giảm. Cụ thể, nếu đại lí mua x điện thoại thì giá tiền của mỗi điện thoại là \(6000 - 3x\) (nghìn đồng), \(x \in {\mathbb{N}^*},x < 2000\). Đại lí nhập cùng một lúc bao nhiêu chiếc điện thoại thì hãng có thể thu về nhiều tiền nhất từ đại lí đó?
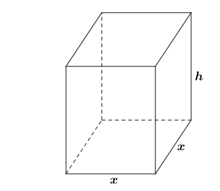
Một hộp sữa dung tích \[1\] lít có dạng hình hộp chữ nhật với đáy là hình vuông cạnh bằng \[x\,\,\left( {{\rm{cm}}} \right)\] và chiều cao \[h\,\,\left( {{\rm{cm}}} \right)\]. Tìm giá trị của \[x\] để diện tích toàn phần của hình hộp là nhỏ nhất.
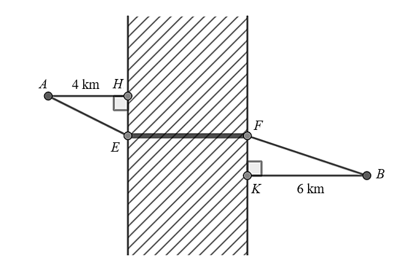
Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu \(EF\) bắc qua sông biết rằng thành phố \(A\) cách con sông một khoảng là \(4\,{\rm{km}}\) và thành phố \(B\) cách con sông một khoảng là \(6\,{\rm{km}}\)(hình vẽ), biết \(HE + KF = 20\,\,{\rm{km}}\) và độ dài \(EF\) không đổi. Hỏi xây cây cầu cách thành phố \(A\) là bao nhiêu kilomet để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường \(AEFB\))? (kết quả làm tròn đến phần chục).