Đề kiểm tra Toán 9 Cánh diều Chương 3 có đáp án - Đề 2
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
hình vuông có diện tích \[0,0144{\rm{ c}}{{\rm{m}}^2}.\] Cạnh của hình vuông đó dài là
\[0,12{\rm{ m}}.\]
\[0,06{\rm{ cm}}.\]
\[0,12{\rm{ cm}}{\rm{.}}\]
\[0,06{\rm{ m}}.\]
Biểu thức \(\sqrt[3]{{{x^3}}},\,\,x > 0\) bằng
\(\left| x \right|\).
\(\)\({x^3}\).
\(x\).
\( - x\).
Điều kiện xác định của biểu thức \(M = \sqrt[3]{{3 - x}} + \frac{1}{{\sqrt {x - 1} }}\) là
\(1 \le x \le 3\).
\(1 < x \le 3\).
\(x > 1\).
\(x \ge 1\).
Giá trị của biểu thức \(N = \sqrt {9 - 4\sqrt 5 } + \sqrt {9 + 4\sqrt 5 } \) bằng
\(N = 4\).
\(N = \sqrt 5 \).
\(N = \sqrt 5 + 4\).
\(N = 2\sqrt 5 \).
Giá trị của biểu thức \[\sqrt {4{x^2}\left( {{y^2} + 6y + 9} \right)} \] tại \(x = 2\,;\,\,y = - \sqrt 7 \) là
\(4\sqrt 7 - 3\).
\[4\left( {\sqrt 7 - 3} \right)\].
\[4\left( {3 - \sqrt 7 } \right)\].
\[8\left( {\sqrt 7 - 3} \right)\].
Định luật thứ ba của Kepler về sự chuyển động của các hành tinh trong hệ Mặt Trời cho biết khoảng cách trung bình \[d\] (triệu dặm) từ một hành tinh quay xung quanh Mặt Trời được tính bởi công thức: \[d = \sqrt[3]{{6{t^2}}}\] với \[t\] (ngày Trái Đất) là thời gian hành tinh đó quay quanh Mặt Trời đúng một vòng. Hỏi Trái Đất cách Mặt Trời bao xa biết Trái Đất ngay một vòng quanh Mặt Trời trong khoảng 365 ngày (làm tròn kết quả đến chữ số thập phân thứ nhất)?
\[92,1\] triệu dặm.
\[92,08\] triệu dặm.
\[92,8\] triệu dặm.
\[92,008\] triệu dặm
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình: \(\sqrt {2{x^2} + x - 6} = x + 2\).
a) Điều kiện của phương trình là \(x \ge 2.\)
b) Bình phương hai vế của phương trình ta được là \({x^2} - 3x - 10 = 0.\)
c) Phương trình có hai nghiệm.
d) Tổng bình phương các nghiệm của phương trình bằng \(20\).
Cho biểu thức \[B = \left( {\frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{4}{{\sqrt x - 4}}} \right):\frac{{x + 16}}{{x + 4\sqrt x }}\] (với \[x > 0\,;\,\,x \ne 16\,).\]
a) Kết quả rút gọn của \[B\] là \[\frac{{\sqrt x }}{{\sqrt x - 4}}\].
b) Giá trị của \[B\] khi \[x = \sqrt {3 - 2\sqrt 2 } \] là \[\frac{{2\sqrt 3 - 1}}{{11}}\].
c) Khi \[x\] là một số chính phương thì \[B\] có giá trị là một số hữu tỉ.
d) Khi \[x > 16\] thì \[B\] có giá trị là một số dương.
Phần 3. Trắc nghiệm trả lời ngắn
Trong mỗi câu hỏi, thí sinh viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Theo quy định, bán kính trái bóng rổ của nữ nhỏ hơn của nam. Bán kính của trái bóng rổ được cho bởi công thức:
\(r = \sqrt[3]{{\frac{{3V}}{{4\pi }}}}\).
Trong đó, \(r\) là bán kính của trái bóng rổ tính bằng \((1\,\,{\rm{inch}} = 2,54\;{\rm{cm}}),\,\,\,V\) là thể tích không khí được chứa trong trái bóng tính bằng \({\rm{inc}}{{\rm{h}}^3}\)). Tính bán kính của trái bóng rổ nữ biết nó chứa được 413 \({\rm{inc}}{{\rm{h}}^3}\) không khí.
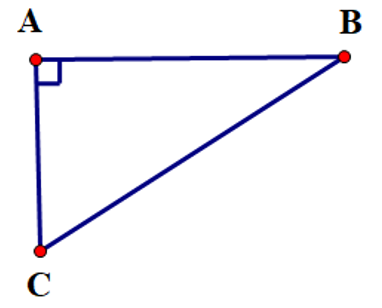
Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí \(A\) đến trường. Trường của anh An ở vị trí \(B\) và trường của em Bình ở vị trí \(C\) theo hai hướng vuông góc với nhau (như hình vẽ). Anh An đi với tốc độ \(4\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 15 phút. Em Bình đi với tốc độ \(3\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) và đến trường sau 12 phút. Tính khoảng cách \(BC\) giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).
Sóng thần (Tsunami) là một loạt các đợt sóng tạo nên khi một thể tích lớn của nước đại dương bị dịch chuyển chớp nhoáng trên một quy mô lớn. Động đất cùng những dịch chuyển địa chất lớn bên trên hoặc bên dưới mặt nước, núi lửa phun và va chạm thiên thạch đều có khả năng gây ra sóng thần. Cơn sóng thần khởi phát từ dưới đáy biển sâu, khi còn ngoài xa khơi, sóng có biên độ (chiều cao sóng) khá nhỏ nhưng chiều dài của cơn sóng lên đến hàng trăm kilomet. Con sóng đi qua đại dương với tốc độ trung bình 500 dặm một giờ. Khi tiến tới đất liền, đáy biển trở nên nông, con sóng không còn dịch chuyển nhanh được nữa, vì thế nó bắt đầu "dựng đứng lên" có thể đạt chiều cao một tòa nhà sáu tầng hay hơn nữa và tàn phá khủng khiếp.
Tốc độ của con sóng thần và chiều sâu của đại dương liên hệ bởi công thức: \(s = \sqrt {dg} .\)
Trong đó, \(d\) là chiều sâu đại dương tính bằng \({\rm{m;}}\)
\(s\) là vận tốc của sóng thần tính bằng \({\rm{m}}/{\rm{s}}\);
\(g = 9,81\,\;\,{\rm{m}}/{{\rm{s}}^2}\) là gia tốc trọng trường.

Susan Kieffer, một chuyên gia về cơ học chất lỏng địa chất của Đại học Illinois tại Mỹ, đã nghiên cứu năng lượng của trận sóng thần Tohoku 2011 tại Nhật Bản. Những tính toán của Kieffer cho thấy tốc độ sóng thần xấp xỉ \(220\;\,{\rm{m}}\,{\rm{/}}\,{\rm{s}}\). Hãy tính độ sâu của đại dương nơi xuất phát con sóng thần này.


