Bài tập ôn tập Toán 9 Cánh diều Chương 3 có đáp án
50 câu hỏi
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Số \(x\) không âm thỏa mãn \(\sqrt x = 6\) là
\(36\).
\(6\).
\(12\).
\(3\).
Căn bậc hai của một số \(a\) không âm là
\(a\).
\(\sqrt a \).
\( - \sqrt a \).
\(\sqrt a \) và \( - \sqrt a \).
Trục căn thức ở mẫu của \(\frac{{15}}{{\sqrt 5 }}\) được kết quả là
\(3\).
\(5\).
\(\sqrt 5 \).
\(3\sqrt 5 \).
Biểu thức \(\sqrt[3]{{{x^3}}},\,\,x > 0\) bằng
\(\left| x \right|\).
\(\)\({x^3}\).
\(x\).
\( - x\).
Rút gọn của biểu thức \(\sqrt {{x^2}} + x - 2025\) với \(x < 0\) là
\(x - 2025\).
\( - x - 2025\).
2025.
\[-2025.\]
Biểu thức \(2{b^2}\sqrt {\frac{{{a^4}}}{{4{b^2}}}} \) với \(b > 0\) bằng
\[\frac{{{a^2}}}{2}\].
\[{a^2}b\].
\[ - {a^2}b\].
\[\frac{{{a^2}{b^2}}}{{{b^2}}}\].
Giá trị của biểu thức \[\sqrt {4{x^2}\left( {{y^2} + 6y + 9} \right)} \] tại \(x = 2\,;\,\,y = - \sqrt 7 \) là
\(4\sqrt 7 - 3\).
\[4\left( {\sqrt 7 - 3} \right)\].
\[4\left( {3 - \sqrt 7 } \right)\].
\[8\left( {\sqrt 7 - 3} \right)\].
Kết quả của phép tính \(\sqrt {36} \cdot \sqrt {64} \) là
\(36\).
\(6\).
\(8\).
\(48\).
Tốc độ của một chiếc cano và độ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức \(v = 5\sqrt I ,\) trong đó \(I\) là độ dài đường nước sau đuôi cano (mét), \(v\) là vận tốc của cano (m/giây). Khi cano chạy với vận tốc \(54\,\,{\rm{km}}\,{\rm{/}}\,{\rm{h}}\) thì đường sóng nước để lại sau đuôi chiếc cano dài bao nhiêu mét?
\(5\,\,{\rm{m}}.\)
\(5\sqrt 3 \,\,{\rm{m}}.\)
\(9\,\,{\rm{m}}.\)
\(3\sqrt 5 \,\,{\rm{m}}.\)
Kết quả của phép tính \(\frac{{\sqrt {99} }}{{\sqrt {11} }}\) là
\(9\).
\(11\).
\(3\).
\(\sqrt 3 \).
Giá trị của biểu thức \(\sqrt {125} - \sqrt {80} + \sqrt {20} \) là
\(11\sqrt 5 \).
\(15\).
\(3\sqrt 5 \).
\(6\sqrt 5 \).
Với giá trị nào của \[x\] thì biểu thức \(\sqrt {x - 2\sqrt {x - 1} } \) có nghĩa?
\(x \le 0\).
\(x \ge 1\,;\,\,x \ne 0\).
\(x \ge 0\,;\,\,x \ne 1\).
\(x \ge 1\).
Cho \(M = 5\) và \(N = \frac{{\sqrt {50} }}{2}\). Khẳng định nào sau đây là đúng?
\(M < N\).
\(M + 2 = N\).
\(M = N\).
\(M > N\).
Trục căn thức ở mẫu của \(\frac{2}{{\sqrt 3 - 1}}\) được kết quả là
\(2\left( {\sqrt 3 + 1} \right).\)
\(2\left( {\sqrt 3 - 1} \right).\)
\(\sqrt 3 + 1.\)
\(\sqrt 3 - 1.\)
Thu gọn \(\sqrt[3]{{125{a^3}}}\) ta được
\( - 25{a^3}\).
\(25a\).
\(5a\).
\( - 5a\).
Định luật thứ ba của Kepler về sự chuyển động của các hành tinh trong hệ Mặt Trời cho biết khoảng cách trung bình \[d\] (triệu dặm) từ một hành tinh quay xung quanh Mặt Trời được tính bởi công thức: \[d = \sqrt[3]{{6{t^2}}}\] với \[t\] (ngày Trái Đất) là thời gian hành tinh đó quay quanh Mặt Trời đúng một vòng. Hỏi Trái Đất cách Mặt Trời bao xa biết Trái Đất ngay một vòng quanh Mặt Trời trong khoảng 365 ngày (làm tròn kết quả đến chữ số thập phân thứ nhất)?
\[92,1\] triệu dặm.
\[92,08\] triệu dặm.
\[92,8\] triệu dặm.
\[92,008\] triệu dặm.
Một hình vuông có diện tích \[0,0144{\rm{ c}}{{\rm{m}}^2}.\] Cạnh của hình vuông đó dài là
\[0,12{\rm{ m}}.\]
\[0,06{\rm{ cm}}.\]
\[0,12{\rm{ cm}}{\rm{.}}\]
\[0,06{\rm{ m}}.\]
Điều kiện xác định của biểu thức \(M = \sqrt[3]{{3 - x}} + \frac{1}{{\sqrt {x - 1} }}\) là
\(1 \le x \le 3\).
\(1 < x \le 3\).
\(x > 1\).
\(x \ge 1\).
Kết quả thu gọn của biểu thức \[\left( {\sqrt[3]{3} + 1} \right)\left( {\sqrt[3]{9} + \sqrt[3]{3} + 1} \right)\] là
\[\sqrt[3]{3}\].
1.
9.
4.
Gọi \[S\] là tập các giá trị nguyên của \[x\] thỏa mãn biểu thức \(\sqrt x < 7\). Số phần tử của tập \[S\] là
48.
35.
49.
50.
Khử mẫu của biểu thức \(\sqrt {\frac{3}{{125}}} \) sẽ được kết quả là
\[\frac{{\sqrt {15} }}{{25}}\].
\[\frac{{\sqrt {25} }}{{15}}\].
\[\frac{{\sqrt 5 }}{{25}}\].
\[\frac{{\sqrt 5 }}{{15}}\].
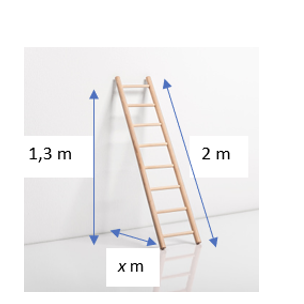
Một cái thang dựa vào tường như hình bên dưới. Biết thang dài \[2\,\,{\mathop{\rm m}\nolimits} \] và tường cao \[1,3\,\,{\rm{m}}.\] Khoảng cách từ chân thang tới góc tường là
\[2,13{\rm{ m}}{\rm{.}}\]
\[1,98{\rm{ m}}.\]
\[1,5{\rm{ m}}.\]
\[1,3{\rm{ m}}.\]
Điều kiện xác định của biểu thức \(K = \sqrt { - {x^2} + 5x - 6} - \frac{1}{{2x + 5}}\) là
\(2 \le x \le 3\).
\(\left\{ \begin{array}{l}x \ge - 2\\x \ne \frac{5}{2}\end{array} \right.\).
\(\left\{ \begin{array}{l}2 \le x \le 3\\x \ne - \frac{5}{2}\end{array} \right.\).
\(x \le 0\).
Rút gọn biểu thức\(B = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + \sqrt 3 \), ta được
\[2\sqrt 3 \].
\[ - 2\sqrt 3 \].
\[ - 2\].
\[2\].
Cho biểu thức \(P = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \frac{1}{{\sqrt x - 1}}} \right):\left( {1 - \frac{{x + 4}}{{x + \sqrt x + 1}}} \right)\). Các giá trị nguyên của \(x\) để \(P\) nhận giá trị nguyên dương là
\(x = 1\,;\,\;x = 36\).
\(x = - 1\,;\,\;x = 36.\)
\(x = 4\,;\,\;x = 6\).
\(x = 16\,;\,\;x = 36\).
Trục căn thức ở mẫu của \(\frac{3}{{\sqrt {10} + \sqrt 7 }}\) được kết quả là
\(\sqrt {10} - \sqrt 7 .\)
\(\sqrt {10} + \sqrt 7 .\)
\(3\left( {\sqrt {10} - \sqrt 7 } \right).\)
\(3\left( {\sqrt {10} + \sqrt 7 } \right).\)
Giá trị của biểu thức \(N = \sqrt {9 - 4\sqrt 5 } + \sqrt {9 + 4\sqrt 5 } \) bằng
\(N = 4\).
\(N = \sqrt 5 \).
\(N = \sqrt 5 + 4\).
\(N = 2\sqrt 5 \).
Cho biểu thức \(C = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{2}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}\) với \(x > 0\,;\,\;x \ne 1.\) Giá trị nhỏ nhất của \(C\) là
\(C = 1\). .
\(C = \sqrt 2 \).
\(C = 2\).
\(C = 2\sqrt 2 \)
Nghiệm của phương trình \(\sqrt {25\left( {x - 1} \right)} = 10\) là
\(x = 2,5\).
\(x = 0,4\).
\(x = 4\).
\(x = 5\).
Trục căn thức ở mẫu biểu thức \[\frac{3}{{6 + \sqrt {3a} }}\] với \(a \ge 0\,;\,\,a \ne 12\) ta được kết quả là
\[\frac{{6 + \sqrt {3a} }}{{12 + a}}\].
\[\frac{{6 - \sqrt {3a} }}{{12 + a}}\].
\[\frac{{6 + \sqrt {3a} }}{{12 - a}}\].
\[\frac{{6 - \sqrt {3a} }}{{12 - a}}\].
Cho biểu thức \[A = \sqrt {\sqrt {17} - 1} \cdot \sqrt {\sqrt {17} + 1} \] và biểu thức \[B = \sqrt {{{\left( {\sqrt 5 - 2} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 - 5} \right)}^2}} .\]
a) Kết quả thực hiện phép tính biểu thức \[A\] là \[16\].
b) Kết quả thực hiện phép tính biểu thức \[B\] là \[3.\]
c) So sánh giá trị biểu thức \[A\] và biểu thức \[B\] ta được \[A > B.\]
d) Kết quả phép tính \[A - 2B\] là \[2.\]
Cho biểu thức \[A = \sqrt {25{x^2}} - 7x.\]
a) Kết quả thực hiện phép tính biểu thức \[A\] là \[5\left| x \right| - 7x\].
b) Với \[x \ge 0\], kết quả rút gọn biểu thức \[A\] là \[2x\].
c) Giá trị của biểu thức \[A\] tại \[x = - 3\] là \[36\].
d) Với \[x < 0\], giá trị của \[x\] để giá trị biểu thức \[A = 24\] là \[2\].
Cho phương trình: \(\sqrt {2{x^2} + x - 6} = x + 2\).
a) Điều kiện của phương trình là \(x \ge 2.\)
b) Bình phương hai vế của phương trình ta được là \({x^2} - 3x - 10 = 0.\)
c) Phương trình có hai nghiệm.
d) Tổng bình phương các nghiệm của phương trình bằng \(20\).
Gọi \({x_1}\) là nghiệm của phương trình \(\sqrt {2x - 1} = \sqrt 3 \). \(\left( 1 \right)\)
\({x_2}\) là nghiệm của phương trình \(\sqrt[3]{{ - 3x + 1}} = \sqrt[3]{2}\). \(\left( 2 \right)\)
a) Phương trình \(\left( 1 \right)\) có một nghiệm \({x_1} = 5\).
b) Phương trình \(\left( 2 \right)\) có một nghiệm \({x_2} = \frac{{ - 1}}{3}\).
c) \({x_1} + {x_2} = \frac{5}{3}\).
d) \({x_1}{x_2} = \frac{2}{3}\).
Cho phương trình \[2\sqrt x - 6 = - 2\].
a) Chuyển vế phương trình trên ta được \[2\sqrt x = 4.\]
b) Nghiệm của phương trình là \[x = 4\].
c) Giá trị của biểu thức \[{x^3}\] với \(x\) là nghiệm của phương trình bằng \[ - 64\].
d) Phương trình đã cho có cùng tập nghiệm với phương trình \[{x^2} - 16 = 0\].
Cho biểu thức \[B = \left( {\frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{4}{{\sqrt x - 4}}} \right):\frac{{x + 16}}{{x + 4\sqrt x }}\] (với \[x > 0\,;\,\,x \ne 16\,).\]
a) Kết quả rút gọn của \[B\] là \[\frac{{\sqrt x }}{{\sqrt x - 4}}\].
b) Giá trị của \[B\] khi \[x = \sqrt {3 - 2\sqrt 2 } \] là \[\frac{{2\sqrt 3 - 1}}{{11}}\].
c) Khi \[x\] là một số chính phương thì \[B\] có giá trị là một số hữu tỉ.
d) Khi \[x > 16\] thì \[B\] có giá trị là một số dương.
Cho biểu thức \[A = \frac{1}{{\sqrt 8 + \sqrt 7 }} + \sqrt {175} - 2\sqrt 2 .\]
a) Kết quả thực hiện phép tính biểu thức \[A\] là \[4\sqrt 7 \].
b) Kết quả thực hiện phép tính biểu thức \[A\] có dạng \[a - b\sqrt 7 \] thì \[a - b = - 4.\]
c) Giá trị của biểu thức \[A\sqrt 7 - \frac{2}{{\sqrt 6 }}\] là \[\frac{{84 - \sqrt 6 }}{3}\].
d) Giá trị của \[x\] để \[Ax - 6\sqrt 7 = 0\] là \[\frac{3}{2}\].
Cho hai biểu thức: \(N = \frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt 3 - \sqrt 2 }} + \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}\) và \(P = \frac{3}{{\sqrt 8 + \sqrt 5 }} + \frac{{5 - \sqrt 5 }}{{\sqrt 5 - 1}}.\)
a) Kết quả phép tính \[N\] là một số nguyên.
b) Kết quả của phép tính biểu thức \[P = 2\sqrt 2 \].
c) Giá trị của biểu thức \[N,\,\,P\] liên hệ với nhau bởi biểu thức \[N = 5P\].
d) Giá trị của biểu thức \[N,\,\,P\] là nghiệm của phương trình \[2{x^2} - 20\sqrt 2 x = 0.\]
Với \(a > 0\,;\,\,b > 0\), cho biểu thức \(M = \sqrt {\frac{a}{b}} + \frac{a}{b} \cdot \sqrt {\frac{b}{a}} .\)
a) Kết quả rút gọn biểu thức là \(\sqrt {\frac{{2a}}{b}} \).
b) Giá trị của biểu thức \(M\) với \[a = 1\,;\,\,\,b = 2\] là \[\sqrt 2 \].
c) Biết \[b \cdot M = 1\], khi đó tích \[ab = \frac{1}{2}\].
d) Nếu \[a = b\] thì giá trị biểu thức \[M = 2\].
Cho biểu thức \(M = \sqrt {x - 1} + \frac{1}{{x - 3}} + \sqrt[3]{{x - 2}}\).
a) Điều kiện xác định của \(\sqrt[3]{{x - 2}}\) là \(x \ge 2.\)
b) Điều kiện của \(x\) để biểu thức \(M\) có nghĩa là \(x \ge 2.\)
c) Khi \(x = 1\) thì giá trị của biểu thức \(M\) là \[\frac{{ - 3}}{2}.\]
d) Khi \(\sqrt[3]{{x - 2}} = 0\) thì giá trị của biểu thức \(M\) là \(0\).
Đường chân trời được xem là một đường thẳng, nơi mà mặt đất và bầu trời giao nhau trong mắt người. Đường chân trời thật ra không tồn tại một cách vật lý, mà đơn giản nó là đường giao nhau giữa bầu trời và mặt đất do giới hạn của mắt nên ở điểm xa tít mắt dường như thấy chúng tiếp xúc với nhau. Do Trái Đất hình cầu nên sự uốn cong bề mặt của nó đã ngăn không cho chúng ta nhìn xa quá một khoảng cách nhất định. Cũng vì lý do đó cho nên khi càng lên cao, tầm quan sát của mắt người càng lớn.
Khoảng cách \(d\) (tính bằng km) từ một người ở vị trí có chiều cao \[h\] (tính bằng mét) nhìn thấy được đường chân trời được cho bởi công thức:
\(d = 3,57\sqrt h \).
Nếu muốn nhìn thấy đường chân trời từ khoảng cách \[25\,\,{\mathop{\rm km}\nolimits} \] thì vị trí quan sát của ngọn hải đăng phải được xây cao bao nhiêu so với mặt nước biển? (làm tròn đến hàng đơn vị)
Vận tốc \(v\,\,({\rm{m}}/{\rm{s}})\) của một tàu lượn di chuyển trên một cung tròn có bán kính \(r\,\,({\rm{m}})\) được cho bởi công thức: \(v = \sqrt {ar} \). Trong đó a là gia tốc của tàu \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) (gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Nó là một trong những đại lượng cơ bản dùng để mô tả chuyển động và là độ biến thiên của vận tốc theo thời gian).
Nếu tàu lượn đang chạy với vận tốc \(v = 14\;\,{\rm{m}}/{\rm{s}}\) và muốn đạt mức gia tốc tối đa cho phép là \(a = 9\,\;{\rm{m}}/{{\rm{s}}^2}\) thì bán kính tối thiểu của cung tròn phải là bao nhiêu để xe không văng ra khỏi đường ray?
Để tính toán thời gian một chu kỳ đong đưa (một chu kỳ đong đưa dây đu được tính từ lúc dây đu bắt đầu được đưa lên cao đến khi dừng hẳn) của một dây đu, người ta sử dụng công thức:
\(T = 2\pi \sqrt {\frac{L}{g}} \).
Trong đó, \[T\] là thời gian một chu kỳ đong đưa (s);
\[L\] là chiều dài của dây đu (m);
\(g = 9,81\;\,{\rm{m}}/{{\rm{s}}^2}.\)
Một người muốn thiết kế một dây đu sao cho một chu kỳ đong đưa của nó kéo dài 4 giây. Hỏi người đó phải làm một dây đu dài bao nhiêu?
Địa y là một dạng kết hợp giữa nấm và một loại sinh vật có thể quang hợp (có thể là tảo lục hay khuẩn lam) trong một mối quan hệ cộng sinh. Địa y tồn tại ở một số môi trường khắc nghiệt nhất thế giới như đài nguyên bắc cực, sa mạc, bờ đá. Chúng rất phong phú trên các lá và cành cây tại rừng mưa và rừng gỗ, trên đá, cả trên tường gạch và đất. Nóc của nhiều tòa nhà cũng có địa y mọc. Địa y rất phổ biến và có thể sống lâu; tuy nhiên, nhiều loại địa y dễ bị tổn thương khi thay đổi thời tiết đột ngột, chúng có thể được các nhà khoa học dùng để đo mức độ ô nhiễm không khí, hay hủy hoại tầng ozone.
Kết quả của sự nóng dần lên của trái đất làm băng tan trên các dòng sông bị đóng băng. Mười hai năm sau khi băng tan, những thực vật nhỏ, được gọi là Địa y, bắt đầu phát triển trên đá. Mỗi nhóm địa y phát triển trên một khoảng đất hình tròn.
Mối quan hệ giữa đường kính \[d,\] tính bằng milimet (mm), của hình tròn và tuổi \[t\] của Địa y có thể biểu diễn tương đối theo công thức:
\(d = 7\sqrt {t - 12} \), với \(t \ge 12\).
An đo đường kính của một số nhóm địa y và thấy có số đo là \[35{\rm{ mm}}.\] Đối với kết quả trên thì băng đã tan cách đó bao nhiêu năm?
Theo quy định, bán kính trái bóng rổ của nữ nhỏ hơn của nam. Bán kính của trái bóng rổ được cho bởi công thức:
\(r = \sqrt[3]{{\frac{{3V}}{{4\pi }}}}\).
Trong đó, \(r\) là bán kính của trái bóng rổ tính bằng \((1\,\,{\rm{inch}} = 2,54\;{\rm{cm}}),\,\,\,V\) là thể tích không khí được chứa trong trái bóng tính bằng \({\rm{inc}}{{\rm{h}}^3}\)). Tính bán kính của trái bóng rổ nữ biết nó chứa được 413 \({\rm{inc}}{{\rm{h}}^3}\) không khí.
Thời gian \(t\) (tính bằng giây) từ khi một người bắt đầu nhảy bungee trên cao cách mặt nước \({\rm{d}}\) (tính bằng \({\rm{m}}\)) đến khi chạm mặt nước được cho bởi công thức:
\(t = \sqrt {\frac{{3\;d}}{{9,8}}} \).
Nếu một người nhảy bungee từ một vị trí khác đến khi chạm mặt nước là 7 giây. Hãy tìm độ cao của người nhảy bungee so với mặt nước.
Vận tốc lăn \(v\) (tính bằng \({\rm{m}}/{\rm{s}}\)) của một vật thể nặng m (tính bằng kg) được tác động một lực \({E_k}\) (gọi là năng lượng Kinetic Energy, ký hiệu \({E_k}\), tính bằng Joule) được cho bởi công thức:
\(v = \sqrt {\frac{{2{E_k}}}{m}} \).
Muốn lăng một quả bowling nặng 3 kg với vận tốc \(6\;{\rm{m}}/{\rm{s}}\), thì cần sử dụng năng lượng Kinetic \({E_k}\) bao nhiêu J?
Tốc độ của một chiếc canô và độ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức \({\rm{v}} = 5\sqrt l \). Trong đó, \(l\) là độ dài đường nước sau đuôi canô (mét), \(v\) là vận tốc canô (m/giây). Khi canô chạy với vận tốc \(54\,\;{\rm{km}}/{\rm{h}}\) thì đường sóng nước để lại sau đuôi chiếc canô dài bao nhiêu mét?
Tốc độ \(v\,\,\left( {{\rm{m}}\,{\rm{/}}\,{\rm{s}}} \right)\) cần có của một vệ tinh để giữ nó chuyển động tròn ổn định trên quỹ đạo với bán kính \(r\,\,({\rm{m}})\) quanh Trái Đất được cho bởi công thức \(v = \sqrt {\frac{{GM}}{r}} \). Biết hằng số hấp dẫn là \(G = 6,67 \cdot {10^{ - 11}}\,\,{\rm{N}}{{\rm{m}}^{\rm{2}}}{\rm{/}}\,{\rm{k}}{{\rm{g}}^{\rm{2}}}\) và khối lượng Trái Đất là \(M = {5,97.10^{24}}\,\,{\rm{kg}}\). Tính tốc độ của một vệ tinh cách tâm Trái Đất \(15,92796 \cdot {10^6}\,{\rm{m}}\,{\rm{.}}\)
Tốc độ tăng trưởng dân số bình quân hàng năm có thể tính theo công thức:
\(\bar r = \sqrt {\frac{{{P_t}}}{{{P_0}}}} - 1\).
Trong đó: \({P_0}\): Dân số thời điểm gốc;
\({P_t}\): Dân số thời điểm năm sau;
\[\bar r\]: Tốc độ tăng trưởng dân số bình quân hàng năm.
Tổng số dân Việt Nam năm 2014 là \[90\,\,728,9\] nghìn người. Tổng số dân Việt Nam năm 2015 là \[91\,\,703,8\] nghìn người.
Hỏi tốc độ tăng trưởng dân số bình quân hàng năm của Việt Nam trong giai đoạn trên là bao nhiêu phần trăm?
