Đề kiểm tra Toán 12 Cánh diều Chương 1 có đáp án - Đề 1
11 câu hỏi
Phần 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
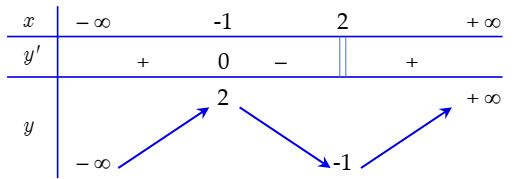
Mệnh đề nào dưới đây là sai?
Hàm số không đạt cực tiểu tại điểm \(x = 2\).
Hàm số đạt cực đại tại điểm \(x = - 1\).
Điểm cực đại của đồ thị hàm số là \(\left( { - 1;2} \right)\).
Giá trị cực đại của hàm số là \(y = 2\).
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
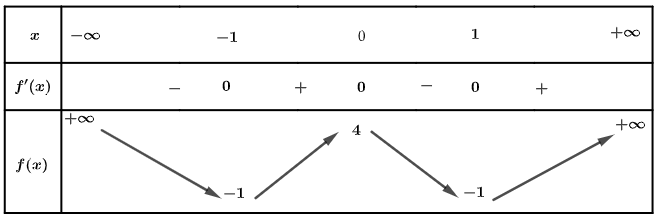
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;0} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
Cho hàm số\(y = \frac{{2x - 1}}{{x + 2}}\). Mệnh đề nào sau đây sai?
Đồ thị hàm số có đúng hai đường tiệm cận.
Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
Hàm số không có giá trị lớn nhất, không có giá trị nhỏ nhất.
Hàm số đồng biến trên tập xác định của nó.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình dưới?
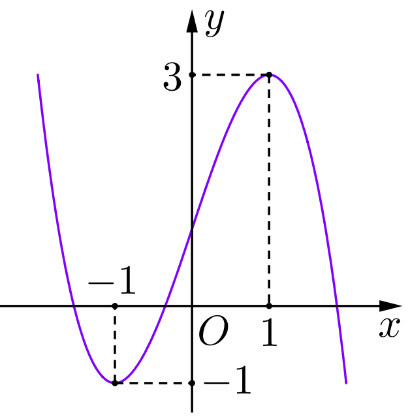
\(y = {x^3} - 3x + 1\).
\(y = - {x^3} + 3x + 1\).
\(y = - {x^4} + 2{x^2} + 1\).
\(y = {x^4} - 2{x^2} + 1\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ.
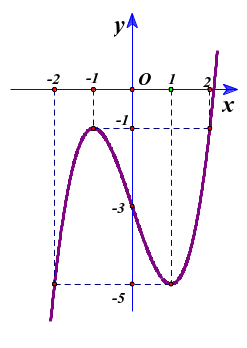
Tìm giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\).
\(m = - 5,M = 0\).
\(m = - 1,M = 0\).
\(m = - 5,M = - 1\).
\(m = - 2,M = 2\).
Đường tiệm cận đứng của đồ thị hàm số \(y = \frac{x}{{x - 1}}\) là
\[x = 1\].
\[y = 1\].
\[y = 0\].
\[x = 0\].
Phần 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
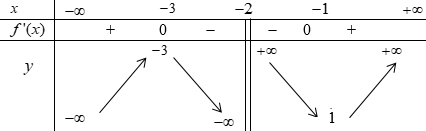
(a)Hàm số đạt cực đại tại điểm \(x = - 3\)và đạt cực tiểu tại \(x = - 1\).
(b)Đồ thị hàm số nhận đường thẳng \(x = - 2\)làm tiệm cận đứng.
(c)Hàm số nghịch biến trên khoảng \(\left( { - 3; - 1} \right)\).
(d)Đồ thị hàm số không có điểm chung với trục hoành.
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao \[250\]km so với bề mặt của Mặt Trăng. Trong khoảng \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao \(h\) của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm \(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\) trong đó \(t\) là thời gian tính bằng giây và \(h\) là độ cao tính bằng kilomet.
(a)Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao lớn nhất mà con tàu đạt được là \(250\)(km).
(b)Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao thấp nhất mà con tàu đạt được tại thời điểm \(t \approx 25\)(s).
(c)Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, vận tốc của con tàu lớn nhất mà con tàu đạt được là \(10,33\,\)(km/s).
(d)Trong \(50\) giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao con tàu đạt được khi vận tốc của con tàu lớn nhất là \(139,37\,\)(km).
Phần 3. Trắc nghiệm trả lời ngắn
Một chất điểm chuyển động theo quy luật \(S\left( t \right) = 6{t^2} - {t^3}\). Vận tốc \(v\)(m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm \(t\)(s) bằng bao nhiêu giây?
Giả sử chi phí đặt hàng và vận chuyển \[C\] (đơn vị: triệu đồng) của một linh kiện được sử dụng trong sản xuất một sản phẩm được xác định theo công thức
\(C = \frac{{19200000}}{{{x^2}}} + \frac{{27x}}{{x + 3000}},\,\,x \ge 1\).
Trong đó \(x\) là số linh kiện được đặt hàng và vận chuyển. Tìm \(x\) để chi phí đặt hàng và vận chuyển cho mỗi linh kiện trên là nhỏ nhất.
Một con cá hồi bơi ngược dòng (từ nơi sinh sống) vượt khoảng cách \[300\,{\rm{km}}\]để tới nơi sinh sản. Vận tốc dòng nước là \[6\,{\rm{km/h}}\]. Giả sử vận tốc bơi của cá khi nước đứng yên là \[v{\rm{ km/h}}\] thì năng lượng tiêu hao của cả trong \(t\) giờ cho bởi công thức \(E\left( v \right) = c{v^3}t\) trong đó \(c\) là hàng số cho trước. \(E\) tính hằng Jun. Tình vận tốc bơi của cá khi nước đứng yên (đơn vị: km/h), để năng lượng của cá tiêu hao ít nhất?