Bài tập ôn tập Toán 12 Cánh diều Chương 1 có đáp án
55 câu hỏi
A. Trắc nghiệm
Dạng 1. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
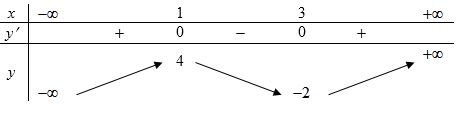
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào sau đây?
\(\left( {3; + \infty } \right)\).
\(\left( {1;3} \right)\).
\(\left( { - \infty ;4} \right)\).
\(\left( {0; + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\]có bảng biến thiên như sau:
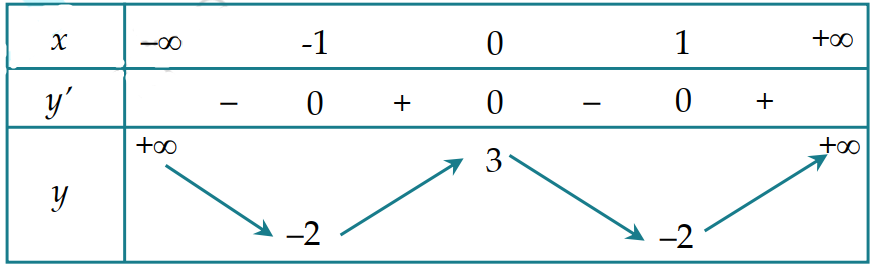
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\[\left( {0\,;1} \right)\].
\[\left( { - 1;0} \right)\].
\[\left( {1; + \infty } \right)\].
\[\left( {0; + \infty } \right)\].
Khẳng định nào sau đây đúng về tính đơn điệu của hàm số \[y = \frac{{x + 2}}{{x - 1}}\]?
Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\]\[ \cup \]\[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
Hàm số nghịch biến trên các khoảng \[\left( { - \infty ; - 1} \right)\] và \[\left( { - 1; + \infty } \right)\].
Cho hàm số \[y = f\left( x \right)\] xác định trên đoạn \[\left[ { - 1;3} \right]\] và đồng biến trên khoảng \[\left( {1;3} \right)\]. Mệnh đề nào dưới đây đúng?
\[f\left( 0 \right) > f\left( 1 \right)\].
\[f\left( 2 \right) < f\left( 3 \right)\].
\[f\left( { - 1} \right) = f\left( 1 \right)\].
\[f\left( { - 1} \right) > f\left( 3 \right)\].
Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau:
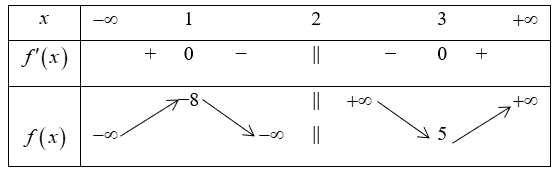
Giá trị cực tiểu của hàm số đã cho bằng
\[ - 8\].
\[5\].
\[3\].
\[1\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
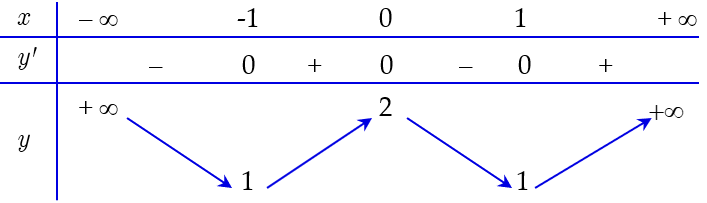
Xác định số điểm cực trị của đồ thị \(y = f\left( x \right)\).
\(6\).
\(3\).
\(1\).
\(2\).
Cho hàm số có bảng biến thiên như sau:
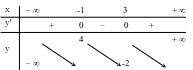
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?
\(x = 3\).
\[x = - 2\].
\(x = 4\).
\(x = - 1\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau:
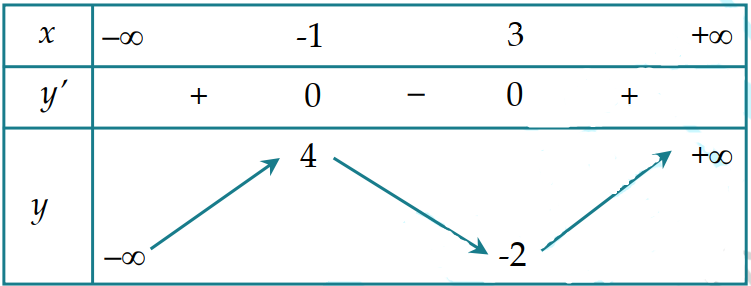
Giá trị cực đại của hàm số đã cho là
\[ - 1\].
\[4\].
\[ - 2\].
\[3\].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau.
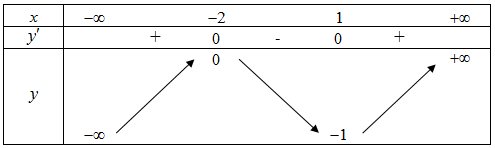
Giá trị cực tiểu của hàm số đã cho bằng
\(1\).
\( - 2\).
\(0\).
\( - 1\).
Hàm số \(y = f\left( x \right)\) có đạo hàm \(y' = {\left( {x - 1} \right)^2}\). Mệnh đề nào sau đây đúng?
Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên \(\mathbb{R}\).
Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\) và đồng biến trên \(\left( {1; + \infty } \right)\).
Hàm số đồng biến trên \(\mathbb{R}\).
Cho hàm số \(f\left( x \right)\) có \(f'\left( x \right) = {x^2}\left( {{x^2} - 1} \right)\) với mọi số thực \(x\). Số điểm cực đại của đồ thị hàm số đã cho là
\(2.\)
\(3.\)
\[1.\]
\[4.\]
Cho hàm số \(y = {x^3} + 1\). Mệnh đề nào dưới đây là mệnh đề đúng?
Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới.
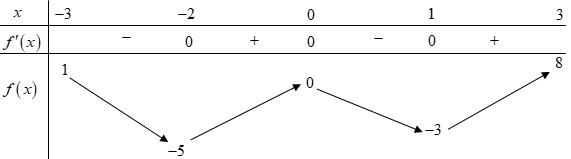
Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 3\,;3} \right]\) bằng
\(0\).
\(3\).
\(1\).
\(8\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 4;2} \right]\) và có đồ thị như hình vẽ.
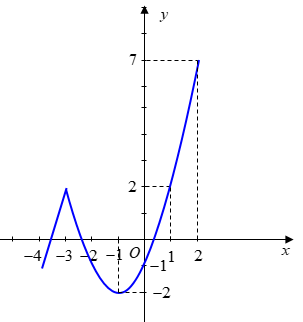
Khi đó \(\mathop {\max }\limits_{\left[ { - 4; - 1} \right]} f\left( x \right) + \mathop {\min }\limits_{\left[ { - 4;2} \right]} f\left( x \right)\) bằng
\(1\).
\(0\).
\(2\).
\(5\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {1;5} \right]\) và có đồ thị như hình vẽ.
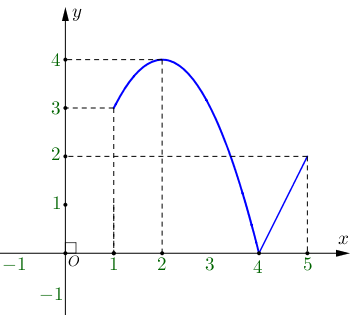
Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {1;5} \right]\). Giá trị \(M - m\) bằng
\[2\].
\[1\].
\(4\).
\(\,5\).
Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\] và có đồ thị như hình vẽ.
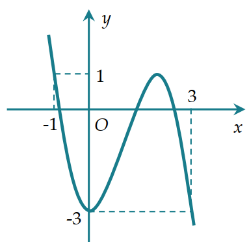
Giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên \[\left[ { - 1;3} \right]\] bằng
\( - 1\).
\(1\).
\( - 3\).
\(3\).
Giá trị lớn nhất của hàm số \(y = \frac{{3x - 1}}{{x - 3}}\) trên đoạn \(\left[ {0;2} \right]\) là
\(5\).
\(\frac{1}{3}\).
\( - \frac{1}{3}\).
\( - 5\).
Giá trị lớn nhất của hàm số \(y = \frac{{{x^2}}}{{x + 1}}\) trên đoạn \(\left[ {0;2} \right]\) là
\(1\).
\(0\).
\( - \frac{4}{3}\).
\(\frac{4}{3}\).
Cho hàm số \[y = f\left( x \right)\] xác định trên tập \[\mathbb{R}\backslash \left\{ { - 1} \right\}\], liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ.
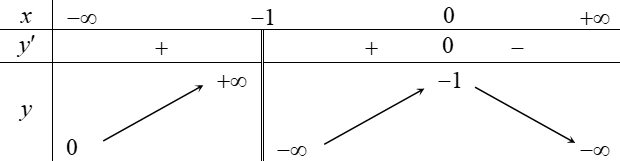
Trong các mệnh đề sau, mệnh đề nào đúng?
Đường thẳng \[x = 0\] và \[x = - 1\] là tiệm cận đứng của đồ thị hàm số.
Đồ thị hàm số không có tiệm cận đứng.
Đồ thị hàm số có duy nhất đường tiệm cận đứng là \[x = 0\].
Đồ thị hàm số có duy nhất đường tiệm cận đứng là \[x = - 1\].
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 2}}{{4 - x}}\) là:
\(y = 2\).
\(y = \frac{3}{4}\).
\(y = - 3\).
\(x = - 3\).
Cho hàm số \(y = \frac{{2x}}{{x + 1}}\) có đồ thị \(\left( C \right)\). Mệnh đề nào sau đây đúng?
\(\left( C \right)\) không có tiệm cận ngang.
\(\left( C \right)\) có hai tiệm cận đứng.
\(\left( C \right)\) không có tiệm cận đứng.
\(\left( C \right)\)có một tiệm cận ngang và một tiệm cận đứng.
Tiệm cận đứng của đồ thị hàm số \[y = \frac{{2x + 1}}{{2x - 1}}\] là:
\[y = 1\].
\[x = 1\].
\[x = \frac{1}{2}\].
\[y = \frac{1}{2}\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình vẽ.
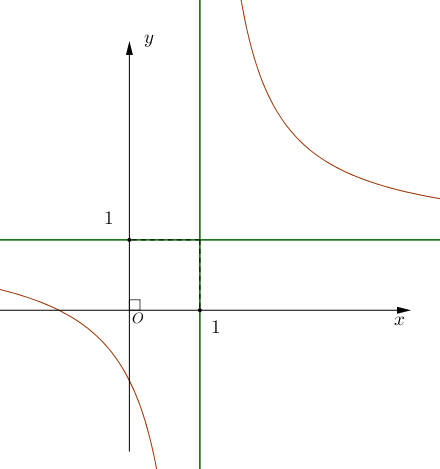
Đồ thị hàm số \(y = f\left( x \right)\) có tiệm cận đứng là đường thẳng nào dưới đây?
\(x = 2\).
\(x = 0\).
\(y = 1\).
\(x = 1\).
Đồ thị hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) có tiệm cận xiên là đường thẳng:
\(y = x\).
\(y = x - 1\).
\(y = 2x - 1\).
\(y = x + 1\).
Đường cong trong hình vẽ sau là đồ thị của hàm số nào?
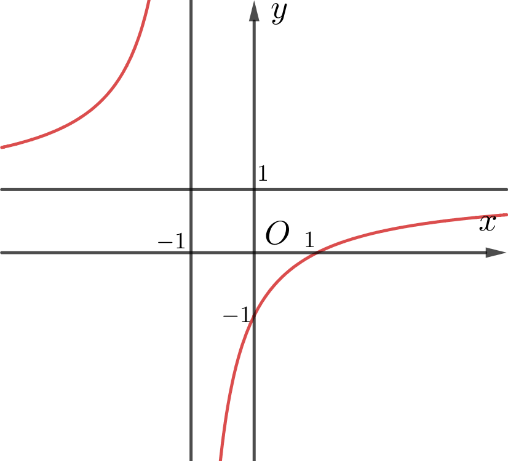
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = \frac{{3x - 1}}{{x + 1}}\).
Hình dưới là đồ thị của một hàm số được liệt kê ở bốn phương án\({\bf{A}},{\bf{B}},{\bf{C}},{\bf{D}}\)dưới đây.
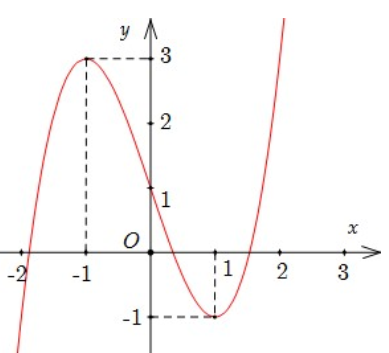
Hàm đó là
\(y = - {x^3} + 3x - 1\).
\(y = {x^3} + 3x + 1\).
\(y = {x^3} - 3x + 1\).
\(y = - {x^3} - 3x + 1\).
Đồ thị hàm số \(y = \frac{{1 - x}}{{x + 1}}\) cắt trục \[Oy\] tại điểm có tọa độ là:
\(\left( {0;1} \right)\).
\(\left( {1;0} \right)\).
\(\left( {0; - 1} \right)\).
\(\left( {1;1} \right)\).
Hàm số nào dưới đây có đồ thị như hình dưới?
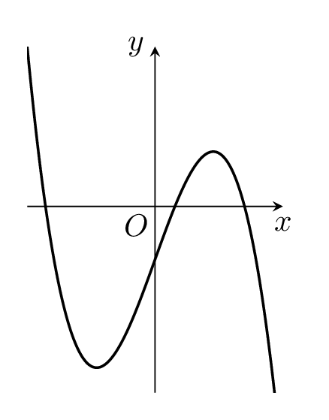
\[y = {x^3} - 3x - 1\].
\[y = - {x^4} + 2{x^2} - 1\].
\[{x^4} - 2{x^2} - 1\].
\[y = - {x^3} + 3x - 1\].
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình dưới.
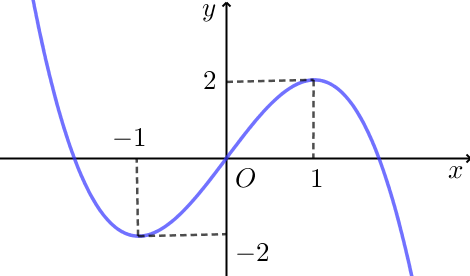
Số nghiệm thực của phương trình \(f\left( x \right) = 2\) là
\(1\).
\(0\).
\(2\).
\(3\).
Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới?
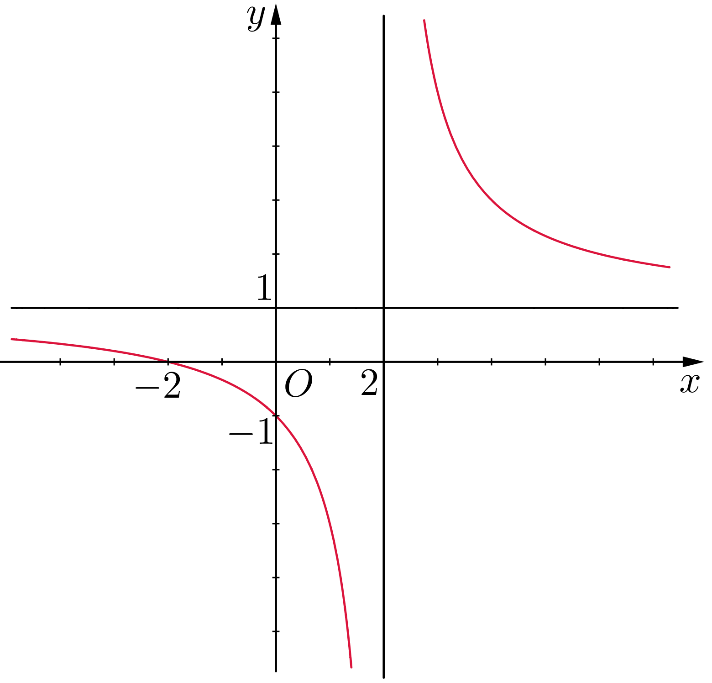
\(y = \frac{{x + 2}}{{x - 2}}\).
\(y = - {x^3} + 3{x^2} - 1\).
\(y = \frac{{x - 1}}{{x - 2}}\).
\(y = {x^4} - 3{x^2} + 2\).
Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ dưới đây:
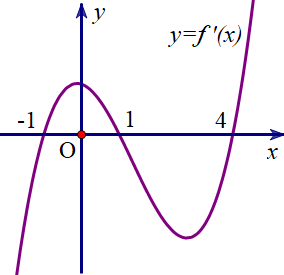
(a)Hàm số \(y = f\left( x \right)\) có hai điểm cực trị.
(b)Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
(c) \(f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)\).
(d)Trên đoạn \(\left[ { - 1;4} \right]\), giá trị lớn nhất của hàm số \(y = f\left( x \right)\) là \(f\left( 1 \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
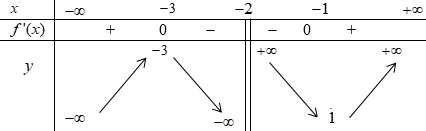
(a)Hàm số đạt cực đại tại điểm \(x = - 3\)và đạt cực tiểu tại \(x = - 1\).
(b)Đồ thị hàm số nhận đường thẳng \(x = - 2\)làm tiệm cận đứng.
(c)Hàm số nghịch biến trên khoảng \(\left( { - 3; - 1} \right)\).
(d)Đồ thị hàm số không có điểm chung với trục hoành.
Cho hàm số \(y = f\left( x \right) = {x^3} - 3x\).
(a) Tập xác định của hàm số là \(\mathbb{R}\).
(b) \(f'\left( x \right) = 3{x^2} + 3\).
(c)\(f'\left( x \right) < 0\) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\), \(f'\left( x \right) > 0\) khi \(x \in \left( { - 1;1} \right)\).
(d) Hàm số đã cho có đồ thị như hình dưới đây.
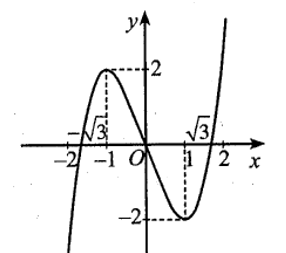
Bác Lâm muốn gò một cái thùng bằng tôn dạng hình hộp chữ nhật không nắp có đáy là hình vuông và đựng đầy được 32 lít nước. Gọi độ dài cạnh đáy của thùng là \(x\left( {{\rm{dm}}} \right)\), chiều cao của thùng là \(h\left( {{\rm{dm}}} \right)\).
(a) Thể tích của thùng là \(V = {x^2} \cdot h\,\,\left( {{\rm{d}}{{\rm{m}}^3}} \right)\).
(b) Tổng diện tích xung quanh và diện tích đáy của thùng là: \(S = 4xh + {x^2}\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right)\).
(c) Đạo hàm của hàm số \(S\left( x \right) = \frac{{128}}{x} + {x^2}\) là \(S'\left( x \right) = \frac{{128}}{{{x^2}}} + 2x\).
(d) Để làm được cái thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là 4 dm.
Nhân ngày quốc tế Phụ nữ 20 – 10 năm 2024. Ông M đã mua tặng vợ một món quà và đặt nó trong một chiếc hộp chữ nhật có thể tích là 32 (đvtt) có đáy là hình vuông và không nắp. Để món quà trở nên đặc biệt và xứng tầm với giá trị của nó, ông quyết định mạ vàng chiếc hộp, biết rằng độ dày của lớp mạ trên mọi điểm của chiếc hộp là không đổi và như nhau. Gọi chiều cao và cạnh đáy của chiếc hộp lần lượt là \[h\] và \[x\].
(a) Công thức tính thể tích chiếc hộp là \[V = {x^2}h\].
(b) Diện tích các mặt ngoài của chiếc hộp là \[S = 2{x^2} + 4xh\].
(c) Diện tích tất cả các mặt được mạ vàng là \[{S_{MV}} = 2{x^2} + 4xh\].
(d) Khi cạnh đáy của chiếc hộp \(x\) lớn hơn \(4\) thì \[x\] càng lớn, lượng vàng được mạ càng tăng.
Một chất điểm chuyển động theo phương trình \(s\left( t \right) = {t^3} - 3{t^2} + 8t + 1\), trong đó \(t\) tính bằng giây và \(s\left( t \right)\) tính bằng mét.
(a) Vận tốc của chất điểm tại thời điểm \(t = 3\left( {\rm{s}} \right)\) bằng \(8{\rm{\;m}}/{\rm{s}}\).
(b) Tại thời điểm mà chất điểm di chuyển được 13 m, vận tốc khi đó bằng \(8{\rm{\;m}}/{\rm{s}}\).
(c) Vận tốc nhỏ nhất của chất điểm là \(5{\rm{\;m}}/{\rm{s}}\).
(d) Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng \(2{\rm{\;m}}/{{\rm{s}}^2}\).
Nhà máy\(A\) chuyên sản xuất một loại sản phẩm cho nhà máy \(B\). Hai nhà máy thỏa thuận rằng, hằng tháng \(A\) cung cấp cho \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(x\) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm được biểu diễn bởi công thức: \(P\left( x \right) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để \(A\) sản xuất \(x\) tấn sản phẩm trong một tháng là \(C\left( x \right) = 100 + 30x\) triệu đồng (gồm \(100\)triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm).
(a) Chi phí để \(A\) sản xuất \(10\) tấn sản phẩm trong một tháng là \(400\)triệu đồng.
(b) Số tiền \(A\) thu được khi bán \(10\) tấn sản phẩm cho \(B\) là \(600\)triệu đồng.
(c) Lợi nhuận mà \(A\) thu được khi bán \(x\) tấn sản phẩm \(\left( {0 \le x \le 100} \right)\) cho \(B\) được biểu diễn bởi công thức \(H\left( x \right) = - 0,001{x^3} + 15x - 100\).
(d) Bên \(A\) bán cho \(B\) khoảng \(70,7\) tấn sản phẩmmỗi tháng thì thu được lợi nhuận lớn nhất.
Một tấm kẽm hình vuông \(ABCD\) có cạnh bằng \(30\;{\rm{cm}}\). Người ta gập tấm kẽm theo hai cạnh \[EF\] và \(GH\) cho đến khi \(AD\) và \(BC\) trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy.
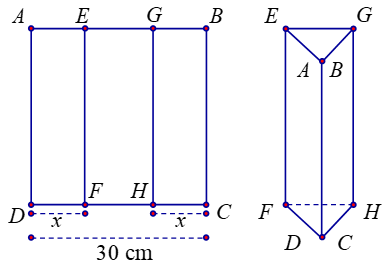
(a) Thể tích khối trụ được tính bằng công thức \(V = 30S\) trong đó \(S\) là diện tích của tam giác \(AEG\).
(b) Diện tích của tam giác \(AEG\) bằng: \(\sqrt {30} .\sqrt {{{\left( {15 - x} \right)}^2}\left( {2x - 15} \right)} \).
(c) Giá trị của \(x\) để thể tích khối lăng trụ lớn nhất là \(x = 10\left( {{\rm{cm}}} \right)\).
(d) Thể tích khối lăng trụ lớn nhất bằng \(1250\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Để làm một cửa sổ có dạng một hình bán nguyệt và một hình chữ nhật ghép lại như hình vẽ bên dưới, người ta dùng \(8 {\rm{m}}\) dây thép để làm các đường viền. Gọi \(x, y\) là độ dài cạnh của khung hình chữ nhật.
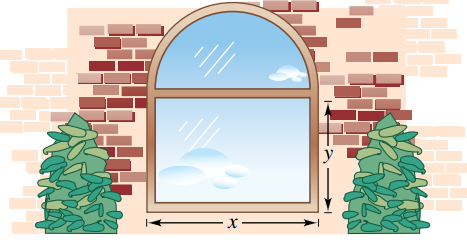
(a) Chiều dài dây để uốn ra bán nguyệt là \(\frac{{\pi x}}{2}\).
(b) Giá trị của \(y\) tính theo \(x\) là \(4 - \frac{{x\left( {4 + \pi } \right)}}{4}\).
(c) Diện tích của cửa sổ là \(S = 4x - {x^2}\).
(d) Khi diện tích của cửa sổ lớn nhất thì \(y = \frac{{16}}{{8 + \pi }}\).
Tại một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách sản xuất cho biết, nếu mỗi ngày cơ sở này sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) nước tinh khiết thì phải chi phí các khoản sau: 5 triệu đồng chi phí cố định; \(0,15\) triệu đồng cho mỗi mét khối sản phẩm; \(0,0005{x^2}\)chi phí bảo dưỡng máy móc. Biết công suất tối đa mỗi ngày của cơ sở này là \(200\,{{\rm{m}}^{\rm{3}}}\). Gọi \(C\left( x \right)\) là chi phí sản xuất \(x\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\) sản phẩm mỗi ngày và \(\overline c \left( x \right)\)là chi phí trung bình mỗi mét khối sản phẩm.
(a)\(C\left( x \right) = 0,0005{x^2} + 0,15x + 5\).
(b) Chi phí sản xuất \(100\,{{\rm{m}}^{\rm{3}}}\) nước tinh khiết là 20 triệu đồng.
(c)\(\overline c \left( x \right) = 0,0005x + 0,15 + \frac{5}{x}\).
(d) Chi phí trung bình giảm xuống khi sản lượng nước tính khiết trong ngày không vượt quá 100 \({{\rm{m}}^3}\).
Dạng 3. Trắc nghiệm trả lời ngắn
Cho \[a \ne 0\], \[{b^2} - 3ac > 0\]. Hàm số \[y = a{x^3} + b{x^2} + cx + d\] có tất cả bao nhiêu điểm cực trị?
Số dân của một thị trấn sau \[t\] năm kể từ năm \[1970\] được ước tính bởi công thức \[f\left( t \right) = \frac{{26t + 10}}{{t + 5}}\] (\[f\left( t \right)\] được tính bằng nghìn người) (Nguồn: Giải tích 12 nâng cao, NXBGD Việt Nam, 2020). Xem \[y = f\left( t \right)\] là một hàm số xác định trên nửa khoảng \[\left[ {0;\, + \infty } \right)\]. Đồ thị hàm số \[y = f\left( t \right)\] có đường tiệm cận ngang là \[y = a\]. Giá trị của \[a\] là bao nhiêu?
Cho đồ thị hàm số \[f\left( x \right) = 5x - 1 + \frac{8}{{x - 1}}\] có tâm đối xứng là \[I\left( {a;\,b} \right)\]. Giá trị của biểu thức \[C = a + 3b\] là bao nhiêu?
Trong khoảng thời gian từ ngày 01/01/2024 đến hết ngày 30/09/2024, nhóm nghiên cứu đã quan sát sự phát triển của một quần thể sinh vật X. Kết quả nghiên cứu chỉ ra rằng, tại ngày thứ t của năm 2024 (tính từ ngày 01/01/2024) số cá thể sinh vật X trong quần thể được ước lượng bởi hàm số \(f\left( t \right) = - \frac{1}{{300}}{t^3} + b{t^2} + ct + 12000\)(con), \(0 \le t \le 365\) và ngày 26/09/2024 là ngày có số lượng cá thể sinh vật X nhiều nhất với 55740 con. Ngày 26/10/2024 số lượng cá thể sinh vật X được ước lượng khoảng bao nhiêu nghìn con? (kết quả làm tròn tới hàng phần chục)
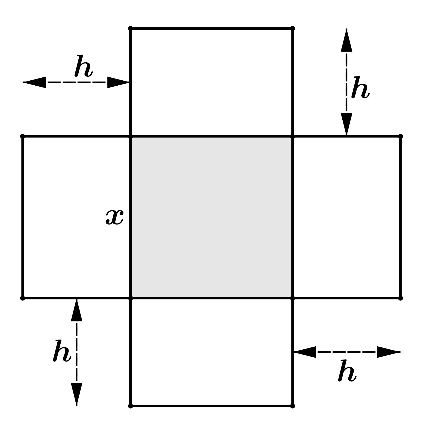
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh \(x\left( {{\rm{cm}}} \right)\), chiều cao là \(h\left( {{\rm{cm}}} \right)\) và thể tích là \(4000{\rm{c}}{{\rm{m}}^{\rm{3}}}.\) Tìm độ dài cạnh hình vuông \(x\) sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
Hai thành phố \(A\) và \(B\) cách nhau một con sông. Người ta xây dựng một cây cầu \(EF\) bắc qua sông biết rằng thành phố \(A\) cách con sông một khoảng là \(4\)km và thành phố \(B\) cách con sông một khoảng là \(6\)km (hình vẽ), biết \(HE + KF = 20\)km và độ dài \(EF\) không đổi. Hỏi xây cây cầu cách thành phố \(A\) là bao nhiêu kilomet để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường \(AEFB\))? (kết quả làm tròn đến phần chục)

Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được \(x\) mét vải lụa \(\left( {1 \le x \le 18} \right)\). Tổng chi phí sản xuất \(x\) mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
\(C\left( x \right) = {x^3} - 3{x^2} - 20x + 500\).
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá \(220\) nghìn đồng/mét. Gọi \(L\left( x \right)\) là lợi nhuận thu được khi bán \(x\) mét vải lụa. Hỏi lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm trong một ngày?
Giả sử doanh số bán hàng (đơn vị triệu đồng) của một sản phẩm mới trong vòng một số năm nhất định tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = 500\left( {{t^2} + m{e^{ - t}}} \right)\), với \(t \ge 0\) là thời gian tính bằng năm kể từ khi phát hành sản phẩm mới, \(m \le 0\) là tham số. Khi đó đạo hàm \(f'\left( t \right)\) sẽ biểu thị tốc độ bán hàng. Biết rằng tốc độ bán hàng luôn tăng trong khoảng thời gian 10 năm đầu phát hành sản phẩm, khi đó giá trị nhỏ nhất của \(m\) bằng bao nhiêu?
Một con cá hồi bơi ngược dòng để vượt khoảng cách là \(100\)km. Vận tốc dòng nước là \(5\)(km/h). Nếu vận tốc bơi của cá khi nước đứng yên là \(v\)(km/h), \(\left( {v > 5} \right)\) thì năng lượng tiêu hao của cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c.{v^3}.t\), trong đó \(c\) là hằng số dương, \(E\) được tính bằng Jun. Biết rằng vận tốc bơi của cá khi nước đứng yên thuộc khoảng \(\left( {a\,;\,b} \right)\) thì năng lượng tiêu hao của cá giảm. Hãy tính giá trị lớn nhất của \(b - a\) (kết quả làm tròn tới hàng phần mười).
Cho hai vị trí \(A,B\) cách nhau \(615{\rm{\;m}}\), cùng nằm về một phía bờ sông như hình vẽ.
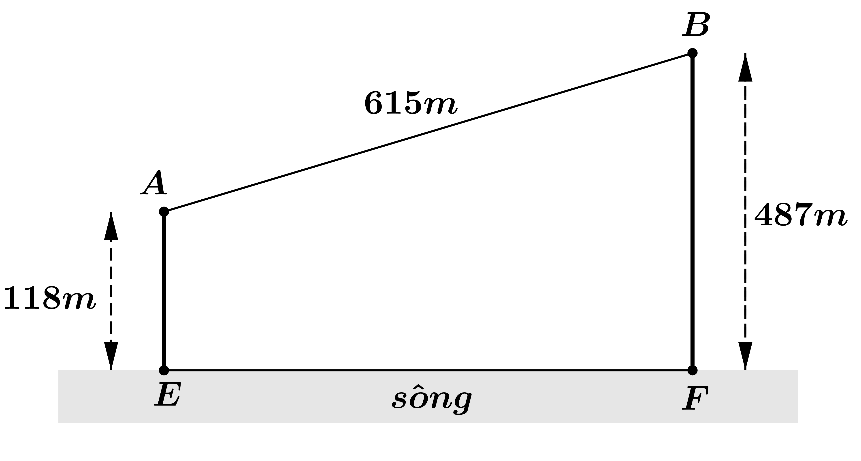
Khoảng cách từ \(A\) và từ \(B\) đến bờ sông lần lượt là \(118{\rm{\;m}}\) và \(487{\rm{\;m}}\). Một người đi từ \(A\) đến bờ sông để lấy nước mang về \(B\). Đoạn đường ngắn nhất là số nguyên dương mà người đó có thể đi là bao nhiêu?
B. Tự luận
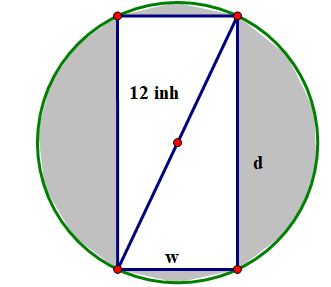
Độ bền \(S\) của dầm gỗ hình chữ nhật tỉ lệ với tích của chiều rộng \(w\) và bình phương chiều sâu \(d\) của nó (xem hinh vẽ). Tìm kích thước của dầm gỗ bền nhất có thể được cắt từ một khúc gỗ hình trụ có đường kính bằng 12 inch.
Một mẫu giấy in hình chữ nhật được thiết kế với vùng in có diện tích \(300\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\), lề trái và lề phải là 2 cm, lề trên và lề dưới là 3 cm. Gọi \(x\left( {{\rm{cm}}} \right)\) là chiều rộng của tờ giấy.
(a) Tính diện tích của tờ giấy theo \(x\).
(b) Kí hiệu diện tích tờ giấy là \(S\left( x \right)\). Khảo sát sự biến thiên của hàm số \(y = S\left( x \right)\).
(c) Tìm kích thước của tờ giấy sao cho nguyên liệu giấy được sử dụng là ít nhất.
Doanh thu \(R\) (USD) từ việc cho thuê \(x\) căn hộ có thể được mô hình hoá bằng hàm số:
\(R = 2x\left( {900 + 32x - {x^2}} \right).\)
(a) Tìm hàm doanh thu biên.
(b) Tìm doanh thu biên khi \(x = 14\) và giải thích ý nghĩa thực tiễn của nó.
(c) Tìm lượng doanh thu tăng thêm khi số căn hộ cho thuê tăng từ 14 lên 15.
Một xưởng mộc dùng gỗ gụ để sản xuất 5 chiếc bàn mỗi ngày. Chi phí cho mỗi lần vận chuyển nguyên liệu là 5000 USD, chi phí để lưu trữ một đơn vị nguyên liệu là 10 USD mỗi ngày, trong đó một đơn vị là lượng nguyên liệu cần thiết để sản xuất 1 chiếc bàn. Hỏi mỗi lần xưởng mộc nên đặt mua bao nhiêu đơn vị nguyên liệu và bao lâu đặt giao nguyên liệu một lần để chi phí trung bình hằng ngày (bao gồm chi phí vận chuyển và chi phí lưu trữ) trong chu kì sản xuất giữa các lần giao hàng là ít nhất?
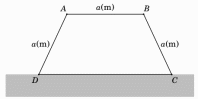
Một bác nông dân có ba tấm lưới B40, mỗi tấm dài \(a\)(m) và muốn rào một mảnh vườn dọc theo bờ sông có dạng hình thang cân \(ABCD\) như hình vẽ dưới đây biết rằng bờ sông là đường thẳng \(CD\) không phải rào lưới. Hỏi bác nông dân đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?