Đề kiểm tra Phép chiếu song song (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Trong không gian, cho hình thang \[ABCD\] có \[AB{\rm{//}}CD,\,\,AB{\rm{ > }}CD\] và mặt phẳng \[\left( P \right)\] không song song với \[AD\]. Phép chiếu song song lên mặt phẳng \[\left( P \right)\] theo phương \[AD\] biến \[ABCD\] thành
một hình thang.
một tam giác.
một đoạn thẳng.
một hình bình hành.
Trong không gian, cho \[\Delta ABC\] nằm trong mặt phẳng song song với mặt phẳng \[\left( P \right)\]. Phép chiếu song song lên mặt phẳng \[\left( P \right)\] theo phương \[l\] (không song song \[\left( P \right)\]) biến \[\Delta ABC\] thành
một tam giác không bằng \[\Delta ABC\].
một tam giác bằng \[\Delta ABC\].
một đoạn thẳng.
một điểm.
Qua phép chiếu song song lên mặt phẳng \[\left( P \right)\], hai đường thẳng chéo nhau \[a\] và \[b\] có hình chiếu là hai đường thẳng \[a',\,b'\]. Mệnh đề nào sau đây là đúng?
\[a'\] và \[b'\] luôn luôn cắt nhau.
\[a'\] và \[b'\] có thể trùng nhau.
\[a'\] và \[b'\] không thể song song.
\[a'\] và \[b'\] có thể cắt nhau hoặc song song nhau.
Qua phép chiếu song song lên mặt phẳng \[\left( P \right)\], hai đường thẳng a và b có hình chiếu là hai đường thẳng song song \[a'\] và \[b'\]. Khi đó:
a và b phải song song với nhau.
a và b phải cắt nhau.
a và b có thể chéo nhau hoặc song song.
a và b không thể song song.
Cho hình chóp \[S.ABCD\] có đáy là hình bình hành. \[M\] là trung điểm của \[SC\]. Hình chiếu song song của điểm \[M\] theo phương \[AB\] lên mặt phẳng \[\left( {SAD} \right)\] là điểm nào sau đây?
\[S\].
Trung điểm của \[SD\].
\[A\].
\[D\].
Cho hình chóp S.ABCD có đáy là hình bình hành, gọi \(M\) là trung điểm của cạnh \(SC\) (như hình vẽ). Hình chiếu song song của điểm \(M\) theo phương \(AC\) lên mặt phẳng \(\left( {SAD} \right)\) là điểm nào sau đây?
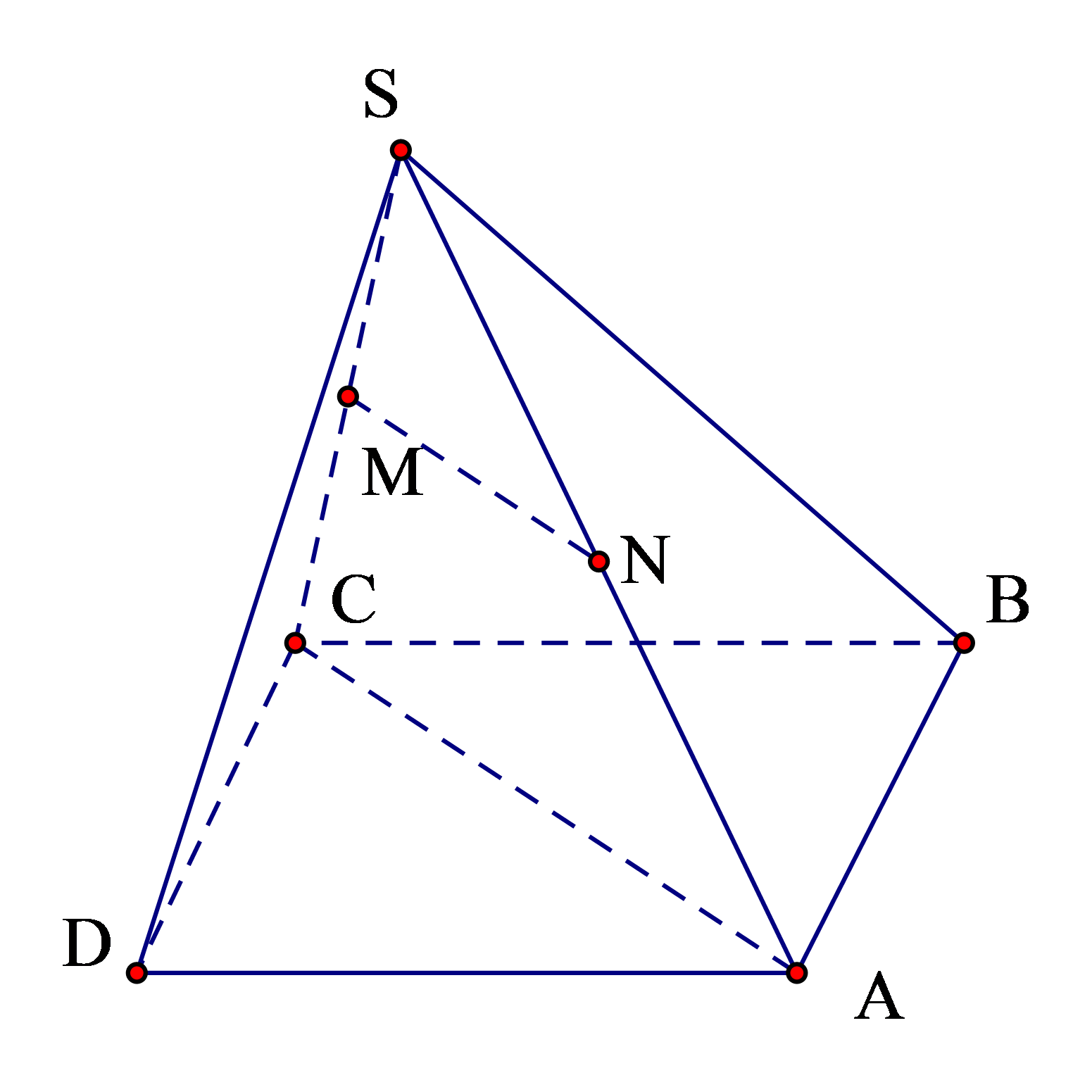
Trung điểm \(SB\).
Trung điểm \(SD\).
Điểm \(D\).
Trung điểm \(SA\).
Cho hình thang ABCD có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\).Chọn khẳng định đúng trong các khẳng định sau?
\({A^\prime }{B^\prime } = {C^\prime }{D^\prime }\).
\(2{A^\prime }{B^\prime } = {C^\prime }{D^\prime }\).
\({A^\prime }{B^\prime } = 2{C^\prime }{D^\prime }\).
\({A^\prime }{B^\prime } < {C^\prime }{D^\prime }\).
Hình nào sau đây là hình biểu diễn của một lục giác đều?
A.  .
.
B. 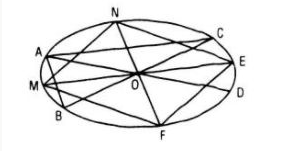 .
.
C. 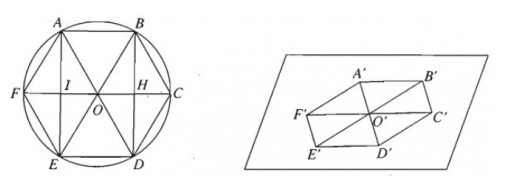 .
.
D. 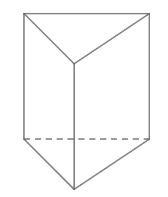 .
.
Tên các hình khối có hình biểu diễn trong hình 10 lần lượt là?
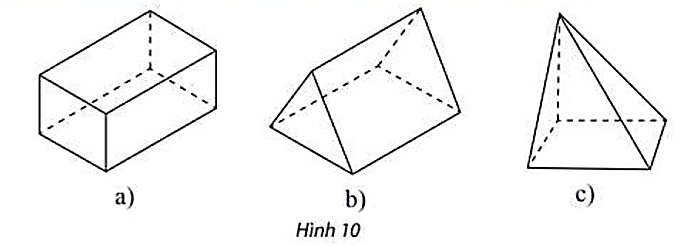
Hình hộp chữ nhật;Hình lăng trụ tứ giác; Hình chóp có đáy là hình thang.
Hình hộp chữ nhật;Hình lăng trụ tam giác; Hình chóp có đáy là hình vuông.
Hình hộp chữ nhật;Hình lăng trụ tam giác; Hình chóp có đáy là hình thang.
Hình hộp chữ nhật;Hình lăng trụ tứ giác; Hình chóp có đáy là hình vuông.
Chiếu song song biến hai đường thẳng song song thành
Hai đường thẳng song song.
Hai đường thẳng trùng nhau
Hai đường thẳng trùng nhau hoặc hai đường thẳng song song.
Hai đường thẳng chéo nhau.
Qua phép chiếu song song, tính chất nào không được bảo toàn?
đồng quy.
song song.
thẳng hàng.
Chéo nhau.
Hình chiếu song song của hình chữ nhật không thể là hình nào trong các hình sau?
Hình thang.
Hình bình hành.
Hình chữ nhật.
Hình thoi.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Các mệnh đề sau đúng/sai?
a) Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thảnh đoạn thẳng.
b) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.
c)Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi thứ tự của ba điểm đó.
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.
Các mệnh đề sau đúng/sai?
a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không là thay đổi thứ tự ba điểm đó.
b) Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song.
c) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.
d) Hình chiếu song song của một đường thẳng là một đường thẳng.
Cho hình chóp S.ABCD có đáy là hình bình hành, trên cạnh \(SA\) lấy điểm \(M\) sao cho \(MA = 2MS\). Gọi \(O\) là tâm của hình bình hành \(ABCD\). Một phép chiếu song song theo phương \(MO\) lên mặt phẳng \((ABCD)\) biến điểm \(S\) thành điểm \(N\).
a) \(N\) là hình chiếu song song của \(S\) lên mặt phẳng \((ABCD)\) theo phương \(OM\).
b) \(\frac{{AO}}{{AN}} = \frac{1}{3}\)
c) \[\frac{{AN}}{{AC}} = 4\]
d) \(\frac{{CN}}{{CA}} = \frac{1}{4}\)
Cho hình lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime };I\) và \({I^\prime }\) lần lượt là trung điểm của đoạn \(AB\) và \({A^\prime }{B^\prime }\).
a) \(A{I^\prime }//I{B^\prime }\)
b) Hình chiếu song song của \(I\) trên mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }} \right)\) phương \({A^\prime }I\) là điểm \({C^\prime }\).
c) Trong mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }} \right)\), vẽ hình bình hành \({A^\prime }{C^\prime }M{I^\prime }\). Suy ra \(ACM{I^\prime }\) là hình bình hành.
d) \(M\)là hình chiếu song song của \(C\) theo phương \(A{I^\prime }\) trên mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }} \right)\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
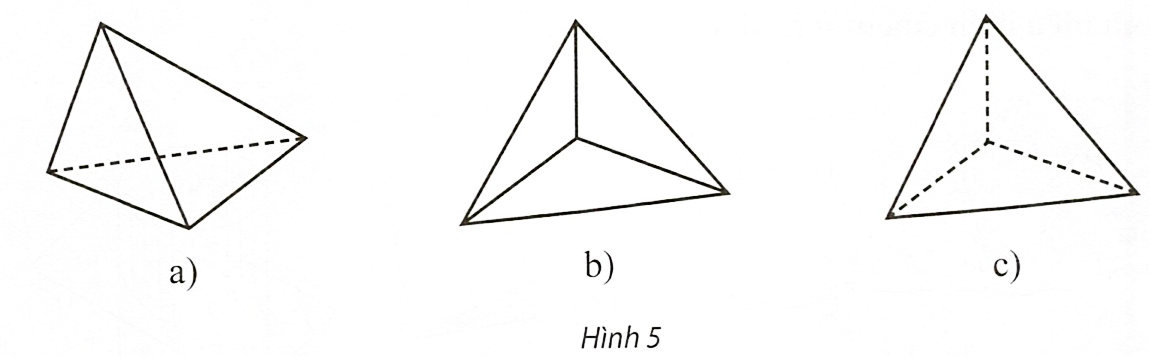
Trong Hình 5, hãy cho biết hình nào là hình biểu diễn của tứ diện?
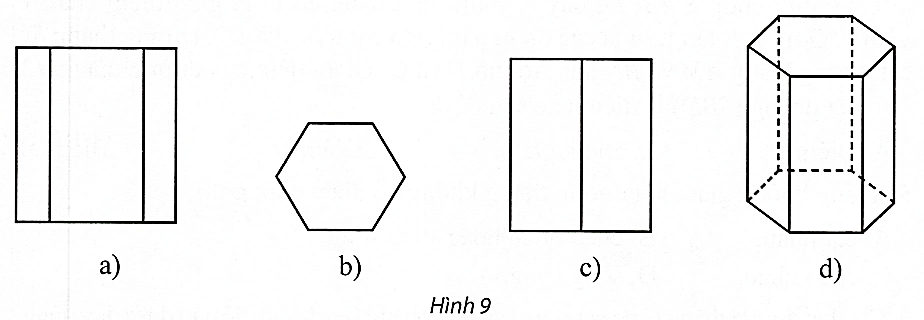
Trong các hình sau, hình nào là hình biểu diễn của hình lăng trụ đứng có đáy là lục giác đều?
Hình biễu diễn của hai đường thẳng chéo nhau có thể là hai đường thẳng song song được không? Vì sao?
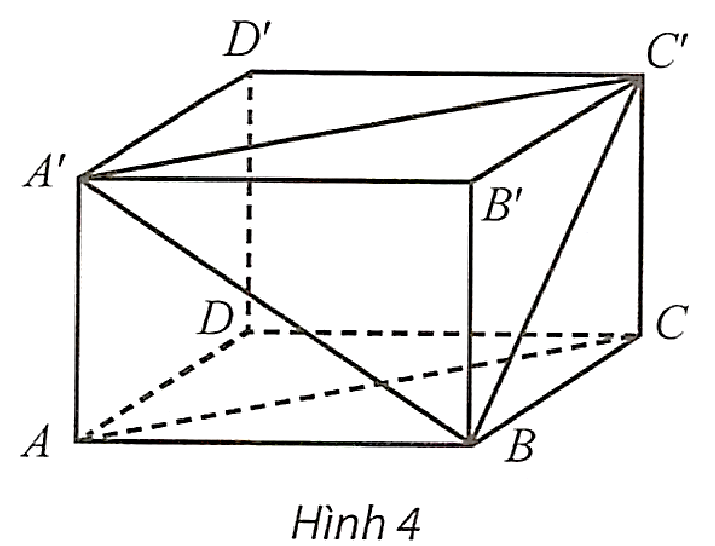
Cho hình hộp \(ABCD.A\prime B\prime C\prime D\prime \). Xác định ảnh của tam giác \(A\prime C\prime B\) qua phép chiếu song song lên mặt phẳng \(\left( {ABCD} \right)\) theo phương \(DD\prime \)
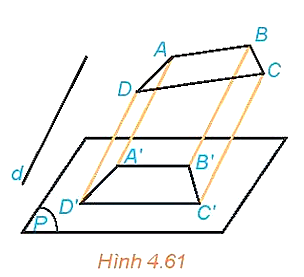
Chứng minh rằng hình chiếu song song của một hình thang là một hình thang \((H.4.61)\).
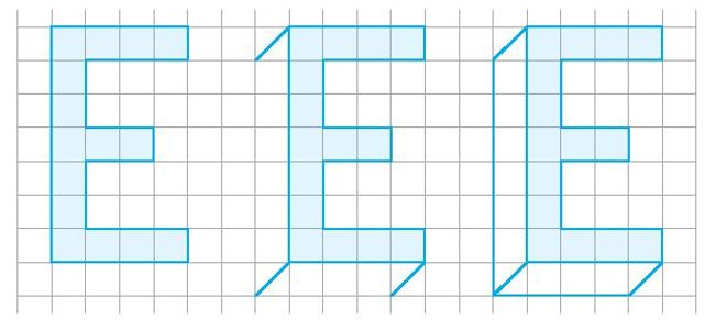
Phép chiếu song song có thể được sử dụng để vẽ dạng nổi (hay dạng 3D) của chữ cái như trong hình dưới đây. Theo phương pháp đó hãy vẽ dạng nổi của một số chữ cái quen thuộc như L, N, T,..