Đề kiểm tra Hệ bất phương trình bậc nhất hai ẩn (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{2x - 3y + 2 > 0}\end{array}} \right.\] là
\[\left( {0;0} \right)\].
\[\left( {1;1} \right)\].
\[\left( { - 1;1} \right)\].
\[\left( { - 1; - 1} \right)\].
Miền nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{\frac{x}{2} + \frac{y}{3} - 1 \ge 0}\\{2(x - 1) + \frac{{3y}}{2} \le 4}\\{x \ge 0}\end{array}} \right.\] là phần mặt phẳng chứa điểm
\(\left( {2;1} \right)\).
\(\left( {0;0} \right)\).
\(\left( {1;1} \right)\).
\(\left( {3;4} \right)\).
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình\[\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.\]?
\[\left( { - 1;4} \right)\].
\[\left( { - 2;4} \right)\].
\[\left( {0;0} \right)\].
\[\left( { - 3;4} \right)\].
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\]?
\[\left( {0;0} \right)\].
\[\left( {1;0} \right)\].
\[\left( {0; - 2} \right)\].
\[\left( {0;2} \right)\].
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - \frac{3}{2}y \ge 1\\4x - 3y \le 2\end{array} \right.\)có tập nghiệm \(S\). Khẳng định nào sau đây là khẳng định đúng ?
\(\left( { - \frac{1}{4}; - 1} \right) \notin S\).
\(S = \left\{ {\left( {x;y} \right)|4x - 3y = 2} \right\}\).
Biểu diễn hình học của \(S\) là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ \[d\], với \[d\] là là đường thẳng \(4x - 3y = 2\).
Biểu diễn hình học của \(S\) là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ \[d\], với \[d\] là là đường thẳng \(4x - 3y = 2\).
Cho hệ \(\left\{ \begin{array}{l}2x + 3y < 5\,\,\,(1)\\x + \frac{3}{2}y < 5\,\,\,(2)\end{array} \right.\). Gọi \({S_1}\) là tập nghiệm của bất phương trình (1), \({S_2}\) là tập nghiệm của bất phương trình (2) và \(S\) là tập nghiệm của hệ thì
\({S_1} \subset {S_2}\).
\({S_2} \subset {S_1}\).
\({S_2} = S\).
\({S_1} \ne S\).
Miền được gạch chéo trong hình bên dưới biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?
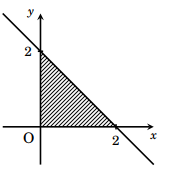
\(\left\{ \begin{array}{l}x > 0\\y > 0\\x + y < 2\end{array} \right.\).
\(\left\{ \begin{array}{l}x > 0\\y > 0\\x + y < 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x > 0\\y > 0\\x + y > 2\end{array} \right.\).
\(\left\{ \begin{array}{l}x < 0\\y > 0\\x + y < 2\end{array} \right.\).
Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là
\(\min F = 1\) khi \(x = 2\), \(y = 3\).
\(\min F = 2\) khi \(x = 0\), \(y = 2\).
\(\min F = 3\) khi \(x = 1\), \(y = 4\).
\(\min F = 0\) khi \(x = 0\), \(y = 0\).
Giá trị nhỏ nhất của biết thức \[F = y - x\] trên miền xác định bởi hệ \[\left\{ {\begin{array}{*{20}{c}}{2x + y \le 2}\\{x - y \le 2}\\{5x + y \ge - 4}\end{array}} \right.\] là
\[{\rm{min }}F = - 3\] khi \[x = 1,y = - 2\].
\[{\rm{min}}\,F = 0\] khi\[x = 0,y = 0\].
\[{\rm{min }}F = - 2\] khi \[x = \frac{4}{3},y = - \frac{2}{3}\].
\[{\rm{min }}F = 8\] khi \[x = - 2,y = 6\].
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\3x + 5y \le 15\\x \ge 0\\y \ge 0\end{array} \right.\). Khẳng định nào sau đây là khẳng định sai?
Trên mặt phẳng tọa độ \(Oxy\), biểu diễn miền nghiệm của hệbất phương trình đã cho là miền tứ giác \(ABCO\) kể cả các cạnh với \(A\left( {0;3} \right)\), \(B\left( {\frac{{25}}{8};\frac{9}{8}} \right)\), \(C\left( {2;0} \right)\) và \(O\left( {0;0} \right)\).
Đường thẳng \(\Delta :x + y = m\) có giao điểm với tứ giác \(ABCO\) kể cả khi \( - 1 \le m \le \frac{{17}}{4}\).
Giá trị lớn nhất của biểu thức \(x + y\), với \(x\) và \(y\) thỏa mãn hệ bất phương trình đã cho là \(\frac{{17}}{4}\).
Giá trị nhỏ nhất của biểu thức \(x + y\), với \(x\) và \(y\) thõa mãn hệ bất phương trình đã cho là 0.
Giá trị lớn nhất của biết thức \[F\left( {x;y} \right) = x + 2y\] với điều kiện \[\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\] là
\[6\].
\[8\].
\[10\].
\[12\].
Một gia đình cần ít nhất \(900\) đơn vị protein và \(400\) đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa \(800\) đơn vị protein và \(200\)đơn vị lipit. Mỗi kilogam thịt lợn chứa \(600\)đơn vị protein và \(400\) đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất \(1,6\) kg thịt bò và \(1,1\) kg thịt lợn. Giá tiền một kg thịt bò là \(160\) nghìn đồng, một kg thịt lợn là \(110\) nghìn đồng. Gọi \(\,x\),\(y\) lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm \(\,x\),\(y\) để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn?
\(x = 0,3\) và \(y = 1,1\).
\(x = 0,3\) và \(y = 0,7\).
\(x = 0,6\) và \(y = 0,7\).
\(x = 1,6\) và \(y = 0,2\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Xét tính đúng, sai của các mệnh đề sau:
a) \((1;0)\) không là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y > 0}\\{y - 2x < 0}\\{3x + 3y - 1 > 0}\end{array}} \right.\)
b) \(( - 1;2)\) là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y > 0}\\{y - 2x < 0}\\{3x + 3y - 1 > 0}\end{array}} \right.\)
c) \((2; - 3)\) là một nghiệm của hệ bất phương trình
d) \((2; - 3)\) không là một nghiệm của hệ bất phương trình\(\left\{ {\begin{array}{*{20}{l}}{2x + y \ge 0}\\{x + y < 0}\\{x + 2y > 2}\end{array}} \right.\)
Cho các hệ bất phương trình sau: , . Khi đó:
a) Miền nghiệm của hệ bất phương trình là tam giác.
b) Điểm \(M(1;1)\) thỏa mãn miền nghiệm của hệ bất phương trình .
c) Miền nghiệm của hệ bất phương trình là tứ giác.
d) Điểm \(O(0;0)\) không thỏa mãn miền nghiệm của hệ bất phương trình .
Xét tính, đúng sai của các mệnh đề sau:
a) Điểm \(M(1;2)\) không thuộc miền nghiệm của hệ bất phương trình\(\left\{ {\begin{array}{*{20}{l}}{x + 3y - 6 > 0}\\{2x + y + 4 > 0}\end{array}} \right.\);
b) Điểm \(M(1;2)\) không thuộc miền nghiệm của hệ bất phương trình\(\left\{ {\begin{array}{*{20}{l}}{x + 3y - 6 < 0}\\{2x + y - 4 < 0}\end{array}} \right.\).
c) Điểm \((0;0)\) là một nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}x + y - 2 \le 0\\2x - 3y + 2 > 0\end{array}\end{array}?} \right.\)
d) Điểm \((1;1)\) là một nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}x + y - 2 \le 0\\2x - 3y + 2 > 0\end{array}\end{array}?} \right.\)
Một gia đình cần ít nhất \(900\;g\) chất protein và \(400\;g\) chất lipit trong thức ăn mỗi ngày. Biết rằng thịt bò chứa \(80\% \) protein và \(20\% \) lipit. Thịt lợn chứa \(60\% \) protein và \(40\% \) lipit. Biết rằng gia đình này chỉ mua nhiều nhất là \(1600\;g\) thịt bò, \(1100\;g\) thịt lợn, giá tiền \(1\;kg\) thịt bò là 45000 đồng, \(1\;kg\) thịt lợn là 35000 đồng. Giả sử gia đình mua \(x\) kg thịt bò và \(y\) kg thịt lợn. Khi đó:
a) là hệ bất phương trình biểu thị các điều kiện của bài toán
b) Miền nghiệm của hệ trên là miền của tam giác
c) Gọi \(T\) (nghìn đồng) là số tiền phải trả cho \(x\) (kilogam) thịt bò và \(y\) (kilogam) thịt lợn. Khi đó, chi phí để mua \(x(\;kg)\) thịt bò và \(y(\;kg)\) thịt lợn là: \(T = 35x + 45y\) (nghìn đồng).
d) Gia đình đó mua \(0,6\;kg\) thịt bò và \(0,7\;kg\) thịt lợn thì chi phí là ít nhất.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Tìm tất cả các giá trị của tham số \(m\) để \(m \le - x + y\) với mọi cặp số \((x;y)\) thoả mãn hệ bất phương trình sau: \(\left\{ {\begin{array}{*{20}{r}}\begin{array}{l} - 2x + y \le 2\\ - x + 2y \le 4\\x + y \le 5\\y \ge 0\end{array}\end{array}} \right.\)
Cho hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}x + y \ge 5\\x - 2y \le 2\\{\rm{ }}y \le 3.\end{array}\end{array}} \right.\left( {II} \right)\). Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \(2x - 5y + m \ge 0\) nghiệm đúng với mọi cặp số \((x;y)\) thoả mãn hệ bất phương trình (II).
Trong một cuộc thi pha chế đồ uống gồm hai loại là \(A\) và \(B\), mỗi đội chơi được sử dụng tối đa \(24\;g\) hương liệu, 9 cốc nước lọc và \(210\;g\) đường. Để pha chế 1 cốc đồ uống loại \(A\) cần 1 cốc nước lọc, \(30\;g\) đường và \(1\;g\) hương liệu. Để pha chế 1 cốc đồ uống loại \(B\) cần 1 cốc nước lọc, \(10\;g\) đường và \(4\;g\) hương liệu. Mỗi cốc đồ uống loại \(A\) nhận được 6 điểm thương, mỗi cốc đồ uống loại \(B\) nhận được 8 điểm thưởng. Để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế bao nhiêu cốc đồ uống mỗi loại?
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi ki-lô-gam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi ki-lô-gam thịt lợn (heo) chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là \(1,6\;kg\) thịt bò và \(1,1\;kg\) thịt lợn; giá \(1\;kg\) thịt bò là 200000 đồng, \(1\;kg\) thịt lợn là 160000 đồng. Hỏi gia đình đó cần mua bao nhiêu ki-lô-gam thịt mỗi loại để đảm bảo cung cấp đủ lượng protein, lipit cho gia đình và có chi phí là ít nhất?
Nhân dịp tết Trung thu, xí nghiệp sản xuất bánh muốn sản xuất hai loại bánh: bánh nướng và bánh dẻo. Để sản xuất hai loại bánh này, xí nghiệp cần: đường, bột mì, trứng, mứt bí, lạp xưởng,. Xí nghiệp đã nhập về \(600\;kg\) bột mì và \(240\;kg\) đường, các nguyên liệu khác luôn đáp ứng được số lượng mà xí nghiệp cần. Mỗi chiếc bánh nướng cần \(120\;g\) bột mì, \(60\;g\) đường. Mỗi chiếc bánh dẻo cần \(160\;g\) bột mì và \(40\;g\) đường. Theo khảo sát thị trường, lượng bánh dẻo tiêu thụ không vượt quá ba lần lượng bánh nướng và sản phẩm của xí nghiệp sản xuất luôn được tiêu thụ hết. Mỗi chiếc bánh nướng lãi 8000 đồng, mỗi chiếc bánh dẻo lãi 6000 đồng, Hãy lập kế hoạch sản xuất cho xí nghiệp để đáp ứng nhu cầu thị trường; đảm bảo lượng bột mì, đường không vượt quá số lượng mà xí nghiệp đã chuẩn bị và vẫn thu được lợi nhuận cao nhất.
Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:
- Mỗi kg sản phẩm loại I cần \(2\;kg\) nguyên liệu và 30 giờ, thu lời được 40 nghìn.
- Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, thu lời được 30 nghìn. Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc tối đa. Nên sản xuất mỗi loại sản phẩm bao nhiêu đề có mức lời cao nhất?