Đề kiểm tra Bài tập cuối chương l (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Mấy giờ rồi?
b) Buôn Mê Thuột là thành phố của Đắk Lắk.
c) \(2019\)là số nguyên tố.
d) Làm việc đi !
\(4\)
\(2.\)
\(3.\)
\(1.\)
Hãy liệt kê các phần tử của tập hợp \(X = \left\{ {x \in \mathbb{Z}|2{x^2} - 3x + 1 = 0} \right\}\).
\(X = \left\{ 0 \right\}\).
\(X = \left\{ 1 \right\}\).
\(X = \left\{ {1;\frac{1}{2}} \right\}\).
\(X = \left\{ {1;\frac{3}{2}} \right\}\).
Cho ba tập hợp E, F, G thỏa mãn: \(E \subset F,F \subset G\) và \(G \subset K\). Khẳng định nào sau đây đúng?
\(G \subset F\).
\(K \subset G\).
\(E = F = G\).
\(E \subset K\).
Cho tập hợp \(A = \left\{ {1;2;3;4} \right\},B = \left\{ {0;2;4} \right\}\), \(C = \left\{ {0;1;2;3;4;5} \right\}\). Quan hệ nào sau đây là đúng?
\(B \subset A \subset C\).
\(B \subset A = C\).
\(\left\{ \begin{array}{l}A \subset C\\B \subset C\end{array} \right.\).
\(A \cup B = C\).
Cho định lí . Chọn khẳng định không đúng.
\[P\left( x \right)\] là điều kiện đủ để có \(Q\left( x \right)\).
\(Q\left( x \right)\)là điều kiện cần để có \[P\left( x \right)\].
\[P\left( x \right)\]là giả thiết và \(Q\left( x \right)\) là kết luận.
\[P\left( x \right)\] là điều kiện cần để có \(Q\left( x \right)\).
Cho mệnh đề\[P:''\exists x \in \mathbb{R},\,{x^2} + 2x + 1 < 0''\]. Lập mệnh đề phủ định của mệnh đề\[P\]và xét tính đúng sai của mệnh đề đó.
\[\overline P :''\forall x \in \mathbb{R},\,{x^2} + 2x + 1 \ge 0''\]và đây là mệnh đề sai.
\[\overline P :''\forall x \in \mathbb{R},\,{x^2} + 2x + 1 > 0''\]và đây là mệnh đề sai.
\[\overline P :''\forall x \in \mathbb{R},\,{x^2} + 2x + 1 \ge 0''\]và đây là mệnh đề đúng.
\[\overline P :''\forall x \in \mathbb{R},\,{x^2} + 2x + 1 > 0''\]và đây là mệnh đề đúng.
Chọn khẳng định đúng trong các khẳng định sau:
\(\forall n \in \mathbb{N}:{n^2} > n\).
\(\forall x \in \mathbb{R}:{x^2} < 2\).
\(\forall x \in \mathbb{Z}:2x > 1\).
\(\exists x \in \mathbb{R}:{x^2} > x\).
Cho tập hợp \(A = \left\{ {{x^2} + 1\backslash x \in \mathbb{N},x \le 5} \right\}\). Hãy liệt kê các phần tử của tập hợp A
\(A = \left\{ {0;1;2;3;4;5} \right\}\).
\(A = \left\{ {1;2;5;10;17;26} \right\}\).
\[A = \left\{ {2;5;10;17;26} \right\}\].
\(A = \left\{ {0;1;4;9;16;25} \right\}\).
Số phần tử của tập hợp: \(A = \left\{ {x \in \mathbb{R}\backslash {{\left( {{x^2} + x} \right)}^2} = {x^2} - 2x + 1} \right\}\)là:
0.
3.
1.
2.
Cho tập hợp \(X = \left\{ {1;2;3;4} \right\}\). Câu nào sau đây đúng?
Số tập con của \(X\) là \(16\).
Số tập con của \(X\) gồm có \(2\) phần tử là \(8\).
Số tập con của \(X\) chứa số \(1\) là \(6\).
Số tập con của \(X\) gồm có \(3\) phần tử là \(2\).
Cho \(A\), \(B\) là hai tập hợp bất kì khác tập rỗng, được biểu diễn theo biểu đồ Ven sau. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?
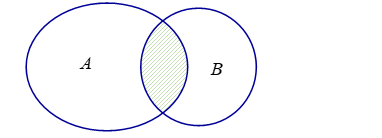
\(A \cup B\).
\(B\backslash A\).
\(A\backslash B\).
\(A \cap B\).
Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán,18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên.
\(15.\)
\(20\).
\(25\).
\(30\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hay cho biết mệnh đề đó đúng hay sai.
a) Trong tam giác tổng ba góc bằng \(180^\circ \)
b) \({(\sqrt 3 - \sqrt {27} )^2}\) là số nguyên
c) 16 chia 3 dư 1.
d) \(\sqrt 5 \) là số vô tỉ.
Cho định lí: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.
Các mệnh đề sau đúng hay sai?
a) Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau.
b) Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.
c) Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
d) Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.
Cho các tập hợp sau \(A = \left\{ {\left. {x \in \mathbb{R}} \right|\left( {2x - {x^2}} \right)\left( {2{x^2} - 3x - 2} \right) = 0} \right\}\) và \(B = \left\{ {\left. {x \in {\mathbb{N}^*}} \right|3 < {n^2} < 30} \right\}\). Khi đó:
a) Tập hợp A có 3 phần tử
b) Tập hợp B có 4 phần tử.
c) Tập hợp \(A \cap B\) có 1 phần tử
d) Tập hợp \(A \cup B\) có 5 phần tử
Lớp \(10{B_1}\) có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Vậy:
a) Số học sinh chỉ giỏi môn Toán là 1 học sinh
b) Số học sinh chỉ giỏi môn Lý là 1 học sinh
c) Số học sinh chỉ giỏi môn Hóa là 2 học sinh
d) Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là 10 học sinh.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho mệnh đề "n chia hết cho 3" với n là số tự nhiên. Phát biểu “Mọi số tự nhiên \(n\) đều chia hết cho 3" có phải là mệnh đề không?
Xét tính đúng sai của các mệnh đề sau:
R: “Nếu tam giác ABC có hai góc bằng 60o thì nó là tam giác đều”;
Cho tập hợp \(A = [m - 3;m + 2),B = ( - 2;5]\). Tìm điều kiện của \(m\) để \(A \subset B\).
Cho các tập hợp \(A = [m - 1;2m + 1)\) và \(B = ( - 2;3)\). Có bao nhiêu giá trị nguyên của \(m\) để \(A \subset B\).
Cho hai tập hợp \(A = [ - 2;3)\) và \(B = [m;m + 5)\). Tìm tất cả các giá trị thực của tham số \(m\) để \(A \cap B \ne \emptyset \).
Một 10C14 có 45 học sinh chuẩn bị cho hội diễn văn nghệ chào mừng ngày nhà giáo Việt Nam 20/11. Trong danh sách đăng kí tham gia tiết mục nhảy Flashmob và tiết mục hát, có 35 học sinh tham gia tiết mục nhảy Flashmob, 10 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong lớp tham gia tiết mục hát? Biết rằng lớp \(10C14\) có bạn Kiệt, Hạ, Toàn, Thiện bị khuyết tật hòa nhập nên không tham gia tiết mục nào.






