Đề kiểm tra Bài tập cuối chương II (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Trong các điểm sau đây, điểm nào thuộc miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x + 3y - 2 \ge 0\\2x + y + 1 \le 0\end{array} \right.\]
\[\left( {0;1} \right)\].
.
\[\left( {1;3} \right)\].
.
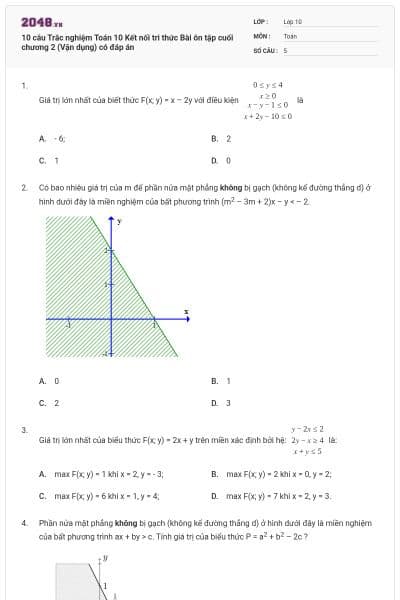
Cho miền gạch chéo như hình vẽ dưới đây
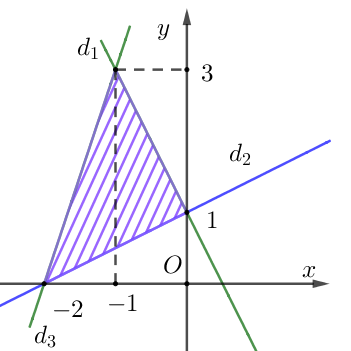
Miền trên đây biểu diễn tập nghiệm của hệ bất phương trình nào?
\(\left\{ \begin{array}{c}2x + y > 1\\ - x + 2y < 2\\3x - y > 6\end{array} \right.\).
\(\left\{ \begin{array}{c}2x + y < 1\\ - x + 2y < 2\\3x - y > - 6\end{array} \right.\).
\(\left\{ \begin{array}{c}2x + y < 1\\ - x + 2y > 2\\3x - y > - 6\end{array} \right.\).
\(\left\{ \begin{array}{c}2x + y > 1\\x - 2y < 2\\3x - y > 6\end{array} \right.\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x + y > 0\\x + 5y - 1 < 0\end{array} \right.\)có tập nghiệm là \(S\). Điểm nào sau đây thuộc tập .
\(\left( { - 1; - 1} \right) \in S\)
\(\left( {2;5} \right) \in S\).
\(\left( {3; - 1} \right) \in S\)
\(\left( { - 1;\frac{2}{5}} \right) \in S\)
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y > 0\\x - 3y \le - 3\\x + y > 5\end{array} \right.\) không chứa điểm nào sau đây?
\(A\left( {3;2} \right)\).
\(B\left( {6;3} \right)\).
\(C\left( {6;4} \right)\).
\(D\left( {5;4} \right)\).
Giá trị nhỏ nhất của biết thức trên \(F = y - x\) miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \le 2}\\{x - y \le 2}\\{5x + y \ge - 4}\end{array}} \right.\) là
\[\min F = 2\] khi \[x = - 1,{\rm{ }}y = 1\].
\[\min F = 2\] khi \[x = 0,{\rm{ }}y = 2\].
\[\min F = - 2\] khi \[x = 1,{\rm{ }}y = - 1\].
\[\min F = - 1\] khi \[x = 0,{\rm{ }}y = - 1\].
Giá trị nhỏ nhất của biết thức \(F = y - x\) trên miền xác định bởi hệ: \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là:
\(\min F = 1\,khi\,x = 2,\,\,y = 3\).
\(\min F = 2\,khi\,x = 0,\,\,y = 2\).
\(\min F = 3\,khi\,x = 1,\,\,y = 4\).
Không tồn tại giá trị nhỏ nhất của \(F\).
Giá trị lớn nhất của biểu thức\[F\left( {x;y} \right) = x + 2y\], với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 4}\\{x \ge 0}\\{x - y - 1 \le 0}\\{x + 2y - 10 \le 0}\end{array}} \right.\) là
\(6\).
\[8\].
\[10\].
\[12\].
Giá trị nhỏ nhất của biểu thức \[F\left( {x;y} \right) = x - 2y\], với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{0 \le y \le 5}\\{x \ge 0}\\{x + y - 2 \ge 0}\\{x - y - 2 \le 0}\end{array}} \right.\) là
\( - 12\).
\[ - 10\].
\[ - 8\].
\[ - 6\].
Biểu thức \(F = y - x\) đạt giá trị nhỏ nhất với điều kiện \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y \le - 2}\\{x - 2y \le 2}\\{x + y \le 5}\\{x \ge 0}\end{array}} \right.\)tại điểm \[S\left( {x;y} \right)\] có toạ độ là
\(\left( {4;1} \right)\).
\(\left( {3;1} \right)\).
\(\left( {2;1} \right)\).
\(\left( {1;1} \right)\).
Giá trị nhỏ nhất của biểu thức \(F = y - x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là
\(\min F = 1\) khi \(x = 2\), \(y = 3\).
\(\min F = 2\) khi \(x = 0\), \(y = 2\).
\(\min F = 3\) khi \(x = 1\), \(y = 4\).
\(\min F = 0\) khi \(x = 0\), \(y = 0\).
Giá trị nhỏ nhất của biết thức \[F = y - x\] trên miền xác định bởi hệ \[\left\{ {\begin{array}{*{20}{c}}{2x + y \le 2}\\{x - y \le 2}\\{5x + y \ge - 4}\end{array}} \right.\] là
\[{\rm{min }}F = - 3\] khi \[x = 1,y = - 2\].
\[{\rm{min}}\,F = 0\] khi\[x = 0,y = 0\].
\[{\rm{min }}F = - 2\] khi \[x = \frac{4}{3},y = - \frac{2}{3}\].
\[{\rm{min }}F = 8\] khi \[x = - 2,y = 6\].
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm \(I\) và \(II\). Mỗi sản phẩm \(I\) bán lãi \(500\) nghìn đồng, mỗi sản phẩm \(II\) bán lãi \(400\) nghìn đồng. Để sản xuất được một sản phẩm \(I\) thì Chiến phải làm việc trong \(3\) giờ, Bình phải làm việc trong \(1\) giờ. Để sản xuất được một sản phẩm \(II\) thì Chiến phải làm việc trong \(2\) giờ, Bình phải làm việc trong \(6\) giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá \(180\) giờ và Bình không thể làm việc quá \(220\) giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.
\[32\] triệu đồng.
\[35\] triệu đồng.
\[14\] triệu đồng.
\[30\] triệu đồng.
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Xét tính đúng, sai của các mệnh đề sau
a) \(\left\{ {\begin{array}{*{20}{l}}{2x + y \le 3}\\{3x - 2y \ge 1}\end{array}} \right.\) là hệ bất phương trình bậc nhất hai ẩn.
b) \(\left\{ {\begin{array}{*{20}{l}}{x + 2 \le 0}\\{y - 3 \ge 1}\end{array}} \right.\)là hệ bất phương trình bậc nhất hai ẩn.
c) \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = 2}\\{2x - 3y = - 1}\end{array}} \right.\) là hệ bất phương trình bậc nhất hai ẩn.
d) \(\left\{ {\begin{array}{*{20}{l}}{2x + 5y \le 30}\\{4x - 3y \ge 5}\\{x \ge 0}\\{y \ge 1}\end{array}} \right.\)là hệ bất phương trình bậc nhất hai ẩn.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.\)có tập nghiệm là \(S\). Các mệnh đề sau đúng hay sai?
a) \(\left( {1;1} \right) \in S\).
b) \(\left( { - 1; - 1} \right) \in S\).
c) \(\left( {1; - \frac{1}{2}} \right) \in S\).
d) \(\left( { - \frac{1}{2};\frac{2}{5}} \right) \in S\).
Cho hệ bất phương trình \[\left\{ \begin{array}{l}x - y > 3\\1 - \frac{1}{2}x + y > 0\end{array} \right.\] có tập nghiệm \[S\]. Các mệnh đề sau đúng hay sai?
a) \[\left( {7;3} \right) \in S\].
b) \[\left( {2\,;1} \right) \in S\].
c) \[\left( {5\,; - 6} \right) \in S\].
d) \[\left( {1\,; - 2} \right) \in S\].
Cho bất phương trình \[x - 2y > - 5\] có tập nghiệm là \[S\]. Mệnh đề sau đúng hay sai?
a) \[\left( {1;\,3} \right) \in S\].
b) \[\left( {0;\,2} \right) \notin S\].
c) \[\left( {2;\,2} \right) \in S\].
d) \[\left( { - 2;\,2} \right) \in S\].
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Trong mặt phẳng \(Oxy, cho tứ giác ABCD có \(A( - 3;0);B(0;2);C(3;1);D(3; - 2)\). Tìm tất cả các giá trị của \(m\) sao cho điểm \(M(m;m - 1)\) nằm trong hình tứ giác \(ABCD\) kể cả 4 cạnh.
Trong một đợt dã ngoại, một trường học cần thuê xe chở 180 người và 8 tấn hàng. Nơi thuê xe có hai loại xe \(A\) và \(B\), trong đó xe \(A\) có 10 chiếc và xe \(B\) có 9 chiếc. Một xe loại \(A\) cho thuê với giá 5 triệu đồng và một xe loại \(B\) cho thuê với giá 4 triệu đồng. Biết rằng mỗi xe loại \(A\) có thể chở tối đa 30 người và 0,8 tấn hàng, mỗi xe loại \(B\) có thể chở tối đa 20 người và 1,6 tấn hàng. Tìm số xe mỗi loại sao cho chi phí thuê là thấp nhất.
Một gia đình cần ít nhất 1200 đơn vị protein và 800 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất \(2,0\;kg\) thịt bò và \(1,5\;kg\) thịt lợn. Giá tiền \(1\;kg\) thịt bò là 200 nghìn đồng, \(1\;kg\) thịt lợn là 100 nghìn đồng. Gọi \(x,y\) lần lượt là số \(kg\) thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính \(4{x^2} + {y^2}\).
Một hộ nông dân định trồng bắp và khoai lang trên diện tích 4ha. Trên diện tích mỗi \(ha\), nếu trồng bắp thì cần 10 công và thu 2 triệu đồng, nếu trồng khoai lang thì cần 15 công và thu 2,5 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 45 công.
Người ta dùng hai loại nguyên liệu để chiết xuất ít nhất \(160\;kg\) hóa chất \(A\) và \(12\;kg\) hóa chất \(B\). Từ mỗi tấn nguyên liệu loại \(I\) giá 5 triệu đồng có thể chiết xuất được \(25\;kg\) chất \(A\) và \(1,2\;kg\) chất \(B\). Từ mỗi tấn nguyên liệu loại \(II\) giá 4 triệu đồng có thể chiết xuất được \(20\;kg\) chất \(A\) và \(2\;kg\) chất \(B\). Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất. Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 9 tấn nguyên liệu loại \(I\) và không quá 7 tấn nguyên liệu loại \(II\).
Một gia đình cần ít nhất \(900\) đơn vị protein và \(400\) đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt lợn chứa \(800\) đơn vị protein và \(200\)đơn vị lipit. Mỗi kg cá chứa \(600\) đơn vị protein và \(400\)đơn vị lipit. Biết rằng gia đình này chỉ mua tối đa \(1,6\) kg thịt lợn và \(1,1\) kg thịt cá. Giá tiền \(1\) kg thịt lợn là \(45\) nghìn đồng và \(1\) kg thịt cá là \(35\) nghìn đồng. Hỏi gia đình đó phải mua bao nhiêu kg mỗi loại để số tiền bỏ ra ít nhất.