Đề kiểm tra Bài tập cuối chương II (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Điểm \(A\left( {2;1} \right)\) thuộc miền nghiệm của bất phương trình nào sau đây?
\(x - y + 1 < 0\).
\( - 2x + y - 2 > 0\).
\(2x - y + 1 > 0\).
\(x - 2y > 0\).
Cho bất phương trình \(x - 2y + 5 > 0\) có tập nghiệm là \(S\).Mệnh đề nào sau đây là đúng?
\(\left( { - 2;2} \right) \in S\).
\(\left( {2;2} \right) \in S\).
\(\left( { - 2;4} \right) \in S\).
\(\left( {1;3} \right) \in S\).
Miền nghiệm của bất phương trình \(5\left( {x + 2} \right) - 9 < 2x - 2y + 7\)không chứa điểm nào trong các điểm sau?
\(\left( {2\,;\,\,3} \right)\).
\(\left( { - 2\,;\,\,1} \right)\).
\(\left( {2\,;\,\, - 1} \right)\).
\(\left( {0\,;\,\,0} \right)\).
Miền nghiệm của bất phương trình \[3\left( {x - 1} \right) + 4\left( {y - 2} \right) < 5x - 3\] là nửa mặt phẳng chứa điểm
\(Q\left( { - 5;3} \right)\).
\(O\left( {0;0} \right)\).
\(N\left( { - 4;2} \right)\).
\(P\left( { - 2;2} \right)\).
Đường thẳng d: 2x - y = 2chia mặt phẳng tọa độ thành hai miền I, II có bờ là đường thẳng d. Xác định miền nghiệm của bất phương trình .
Nửa mặt phẳng I bỏ đi đường thẳng d.
Nửa mặt phẳng I kể cả bờ d.
Nửa mặt phẳng II kể cả bờ d.
Nửa mặt phẳng II bỏ đi đường thẳng d.
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình \(2x + y - 1 < 0\)?
\(Q\left( {1\;;\;1} \right)\).
\(M\left( {1\;;\; - 2} \right)\).
\(P\left( {2\;;\; - 2} \right)\).
\(N\left( {1\;;\;0} \right)\).
Cho bất phương trình \(x - 2y + 5 > 0\) có tập nghiệm là \(S\). Mệnh đề nào sau đây là đúng?
\(\left( { - 2\,;\,2} \right) \in S\).
\(\left( {2\,;\,2} \right) \in S\).
\(\left( { - 2\,;\,4} \right) \in S\).
\(\left( {1\,;\,3} \right) \in S\).
Hình vẽ nào sau đây biểu diễn miền nghiệm của bất phương trình \(2x - 3y - 6 \le 0\)?
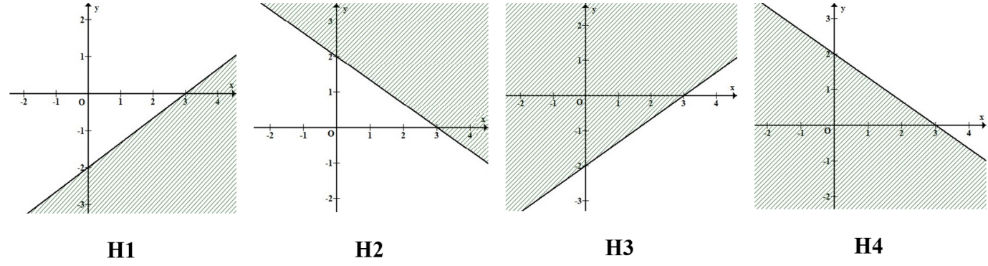
H1
H2
H3
H4
Miền của bất phương trình \(2x + y > 1\)không chứa điểm nào sau đây?
\[C\left( {3;3} \right)\].
\(D\left( { - 1; - 1} \right)\).
\(A\left( {1;1} \right)\).
\(B\left( {2;2} \right)\).
Cặp số \(\left( {1\,;\, - 1} \right)\)thuộc miền nghiệm của bất phương trình nào sau đây?
\(x + y - 3 > 0\).
\( - x - 3y - 1 < 0\).
\( - x - y < 0\).
\(x + 3y + 1 < 0\).
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình \(2x + y - 1 < 0\)?
\(Q\left( {1;1} \right)\).
\(M\left( {1; - 2} \right)\).
\(P\left( {2; - 2} \right)\).
\(N\left( {1;0} \right)\).
Cặp số nào dưới đây là một nghiệm của bất phương trình: \[2x - y > 3\].
\[\left( {3;1} \right)\].
\[\left( {0; - 2} \right)\]
\[\left( {1;1} \right)\].
\[\left( {2;1} \right)\].
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ \(A\) thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ \(B\) thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi \(x,y\) theo thứ tự là số lần người chơi chọn được chữ \(A\) và chữ \(B\). Khi đó:
a) Tổng số điểm người chơi đạt được khi chọn chữ \(A\) là \(3x\), tổng số điểm người chơi bị trừ khi chọn chữ \(B\) là \(y\).
b) Bất phương trình bậc nhất hai ẩn \(x,y\) trong tình huống người chơi chiến thắng là
c) Người chơi chọn được chữ \(A\) 7 lần và chọn được chữ \(B\) 1 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
d) Người chơi chọn được chữ \(A\) 8 lần và chọn được chữ \(B\) 3 lần thì người đó vừa đủ điểm dành chiến thắng trò chơi.
Xét tính đúng, sai của các mệnh đề sau:
a) \(2x - 3y + 4 \le 0\) là bất phương trình bậc nhất hai ẩn.
b) \(6{x^2} + 2y - 4 < 0\)là bất phương trình bậc nhất hai ẩn.
c) \(4x + 7 \ge 0\) là bất phương trình bậc nhất hai ẩn.
d) \(\frac{2}{3}x + \frac{1}{7}y - 4 > 0\) không là bất phương trình bậc nhất hai ẩn.
Cho bất phương trình \(4x - 3y \le 5(*)\). Khi đó:
a) \((1; - 1)\)là nghiệm của bất phương trình \((*)\).
b) \((0;0)\)là nghiệm của bất phương trình \((*)\).
c) \((2;1)\)là nghiệm của bất phương trình \((*)\).
d) \((3; - 1)\)là nghiệm của bất phương trình \((*)\).
Cho bất phương trình bậc nhất hai ẩn: \(5x - y + 4 > 0\). Khi đó:
a) \((0;0)\) là một nghiệm của bất phương trình đã cho
b) \((0;1)\) không là một nghiệm của bất phương trình đã cho
c) \((2; - 1)\) không là một nghiệm của bất phương trình đã cho
d) \(\left( {\frac{1}{5};1} \right)\) là một nghiệm của bất phương trình đã cho
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6
Tìm các nghiệm \((x;y)\) của bất phương trình \(\frac{x}{2} + \frac{y}{3} - 1 \le 0\). Trong đó \(x,y\) là các số nguyên dương.
Tìm các giá trị của tham số \(m\) sao cho \(\left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = - 1}\end{array}} \right.\) là nghiệm của bất phương trình \(m\frac{x}{2} - (m + 1)y + 2 \ge 0\)
Cho tam giác ABC có \(A(0;3);B( - 1;2);C(2;1)\). Tìm điều kiện của tham số \(m\) để điểm \(M\left( {m;\frac{{2m - 1}}{2}} \right)\) nằm bên trong tam giác ABC?
Bạn Lan mang 150000 đồng đi nhà sách để mua một số quyển tập và bút. Biết rằng giá một quyển tập là 8000 đồng và giá của một cây bút là 6000 đồng. Bạn Lan có thể mua được tối đa bao nhiêu quyển tập nếu bạn đã mua 10 cây bút.
Biểu thức \(L = y - x\), với \(x\) và \(y\) thỏa mãn hệ bất phương trình \[\left\{ \begin{array}{l}2x + 3y - 6 \le 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\], đạt giá trị lớn nhất là \(a\) và đạt giá trị nhỏ nhất là \(b\).
Cho các giá trị \[x,y\] thỏa mãn điều kiện \[\left\{ \begin{array}{l}x - y + 2 \ge 0\\2x - y - 1 \le 0\\3x - y - 2 \ge 0\end{array} \right.\]. Tìm giá trị lớn nhất của biểu thức \[T = 3x + 2y\].