Đề kiểm tra Bài tập cuối chương 1 (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Một cung tròn có độ dài bằng bán kính. Khi đó số đo bằng rađian của cung tròn đó là
\(1\).
\(\pi \).
\(2\).
\(3\).
Trên đường tròn bán kính bằng \[4\], cung có số đo \[\frac{\pi }{8}\] thì có độ dài là
\[\frac{\pi }{4}\].
\[\frac{\pi }{3}\].
\[\frac{\pi }{{16}}\].
\[\frac{\pi }{2}\].
Trên đường tròn bán kính \(R = 6\), cung \(60^\circ \) có độ dài bằng bao nhiêu?
\(l = \frac{\pi }{2}\).
\(l = 4\pi \).
\(l = 2\pi \).
\(l = \pi \).
Trên đường tròn lượng giác, điểm \(M\) thỏa mãn \(\left( {Ox,OM} \right) = 500^\circ \) thì nằm ở góc phần tư thứ
\[{\rm{I}}\].
\[{\rm{II}}\].
\[{\rm{III}}\].
\[{\rm{IV}}\].
Bánh xe của người đi xe đạp quay được \(2\) vòng trong \(5\) giây. Hỏi trong \(1\) giây, bánh xe quay được một góc bao nhiêu độ?
\(144^\circ \).
\(288^\circ \).
\(36^\circ \).
\(72^\circ \).
Cho góc \(\alpha \) thỏa mãn \(2\pi < \alpha < \frac{{5\pi }}{2}\). Khẳng định nào sau đây sai?
\(\tan \alpha < 0\).
\(\cot \alpha > 0\).
\(\sin \alpha > 0\).
\(\cos \alpha > 0\).
Cho biết \(\tan \alpha = \frac{1}{2}\). Tính \(\cot \alpha \).
\(\cot \alpha = \frac{1}{2}\).
\(\cot \alpha = \sqrt 2 \).
\(\cot \alpha = 2\).
\(\cot \alpha = \frac{1}{4}\).
Tìm khẳng định sai trong các khẳng định sau đây?
\[\tan 45^\circ < \tan 60^\circ \].
\[\cos 45^\circ \le \sin 45^\circ \].
\[\sin 60^\circ < \sin 80^\circ \].
\[\cos 35^\circ > \cos 10^\circ \].
Cho\(\sin a = \frac{1}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính \(\cos a\).
\[\cos a = \frac{{2\sqrt 2 }}{3}\].
\[\cos a = - \frac{{2\sqrt 2 }}{3}\].
\(\cos a = \frac{8}{9}\).
\(\cos a = - \frac{8}{9}\).
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\beta = \frac{\pi }{3},\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{6}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
\(\beta \) và \(\gamma \)
\(\alpha ,\beta ,\gamma \).
\(\beta ,\gamma ,\delta \).
\(\alpha \) và \(\beta \).
Trong các khẳng định sau, khẳng định nào là sai?
\({\rm{sin}}\left( {\pi - \alpha } \right) = {\rm{sin}}\alpha \).
\({\rm{cos}}\left( {\pi - \alpha } \right) = {\rm{cos}}\alpha \).
\({\rm{sin}}\left( {\pi + \alpha } \right) = - {\rm{sin}}\alpha \).
\({\rm{cos}}\left( {\pi + \alpha } \right) = - {\rm{cos}}\alpha \).
Rút gọn biểu thức \(M = {\rm{cos}}\left( {a + b} \right){\rm{cos}}\left( {a - b} \right) - {\rm{sin}}\left( {a + b} \right){\rm{sin}}\left( {a - b} \right)\), ta được
\(M = {\rm{sin}}4a\).
\(M = 1 - 2{\rm{co}}{{\rm{s}}^2}a\).
\(M = 1 - 2{\rm{si}}{{\rm{n}}^2}a\).
\(M = {\rm{cos}}4a\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho số đo \(\alpha \) của góc lượng giác \(\left( {Ou,Ov} \right)\) với \(0 \le \alpha \le 2\pi \),
a) Biết một góc lượng giác cùng tia đầu, tia cuối với góc \(\alpha \) có số đo là \(\frac{{33\pi }}{4}\) khi đó \(\alpha = \frac{\pi }{4}\)
b) Biết một góc lượng giác cùng tia đầu, tia cuối với góc \(\alpha \) có số đo là \( - \frac{{291983\pi }}{3}\) khi đó \(\alpha = \frac{\pi }{4}\)
c) Biết một góc lượng giác cùng tia đầu, tia cuối với góc \(\alpha \) có số đo là \( - \frac{{291983\pi }}{3}\) khi đó \(\alpha = \frac{\pi }{3}\)
d) Biết một góc lượng giác cùng tia đầu, tia cuối với góc \(\alpha \) có số đo là \(30\)khi đó \(\alpha > 5\)
Cho phương trình lượng giác \({\sin ^2}2x + {\cos ^2}5x = 1\), vậy:
a) Phương trình đã cho tương đương với phương trình \(\frac{{1 - \cos 4x}}{2} + \frac{{1 + \cos 10x}}{2} = 1\)
b) Nghiệm dương nhỏ nhất của phương trình là: \(x = \frac{\pi }{7}\)
c) Nghiệm âm lớn nhất của phương trình nhỏ hơn \( - \frac{\pi }{3}\)
d) Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất bằng 0
Cho góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo \( - \frac{\pi }{7}\). Khi đó:
a) \( - \frac{{29\pi }}{7}\) là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho
b) \( - \frac{{22}}{7}\) là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho
c) \(\frac{{6\pi }}{7}\) là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho
d) \(\frac{{41\pi }}{7}\) là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho
Cho phương trình lượng giác \({(\sin x + \cos x)^2} = 2{\cos ^2}3x\), vậy:
a) Phương trình đã cho tương đương với phương trình \(1 + \sin 2x = 3 + \cos 6x\)
b) Nghiệm dương nhỏ nhất của phương trình lớn hơn \(\frac{\pi }{7}\)
c) Nghiệm âm lớn nhất của phương trình là \(x = - \frac{\pi }{8}\)
d) Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất bằng 0
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Với giá trị nào của \[n\] thì đẳng thức sau luôn đúng \[\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} } } = \cos \frac{x}{n}\], \[0 < x < \frac{\pi }{2}\].
Cho các góc \(\alpha \), \(\beta \) thỏa mãn \(\frac{\pi }{2} < \alpha \), \(\beta < \pi \), \[\sin \alpha = \frac{1}{3}\], \[\cos \beta = - \frac{2}{3}\]. Tính \[\sin \left( {\alpha + \beta } \right)\].
Tìm giá trị lớn nhất của biểu thức \({\sin ^4}x + {\cos ^7}x\)
Nếu \[\alpha \] là góc nhọn và \[\sin \frac{\alpha }{2} = \sqrt {\frac{{x - 1}}{{2x}}} \] thì \[\tan \alpha \] bằng bao nhiêu?
Chứng minh biểu thức \[{\sin ^2}x.\tan x + 4{\sin ^2}x - {\tan ^2}x + 3{\cos ^2}x\] không phụ thuộc vào \[x\]
Khi một tia sáng truyền từ ông khí vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới \(i\) liên hệ với góc khúc xạ \(r\) bởi Định luật khúc xạ ánh s \(\frac{{{\rm{sin}}i}}{{{\rm{sin}}r}} = \frac{{{n_2}}}{{{n_1}}}{\rm{.\;}}\)
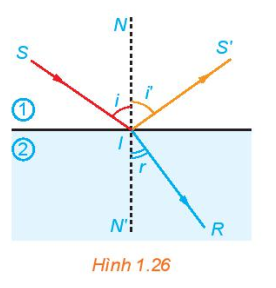
Ở đây, \({n_1}\) và \({n_2}\) tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới \(i = {50^ \circ }\), hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33 .



